题目描述

在一个 $2^k\times 2^k$个方格组成的棋盘中，若恰有一个方格与其他方格不同，则称该方格为一个特殊方格，且称该棋盘为一个特殊棋盘。显然，特殊方格在棋盘上出现的位置有 $4^k$ 种情况，即k>=0，有$4^k$种不同的特殊棋盘。
棋盘覆盖：用4种不同形态（方向不同）的L型骨牌覆盖一个给定的特殊棋盘（即特殊方格的位置已经确定了）上除特殊方格外的所有方格，且任何两个L型骨牌不得重复覆盖。

问题要求输入棋盘的边长n，以及特殊方格的坐标。输出覆盖后的棋盘。

测试样例

输入：

4
1 0

输出：

3 3 4 4
1 3 2 4
6 2 2 5
6 6 5 5

算法原理

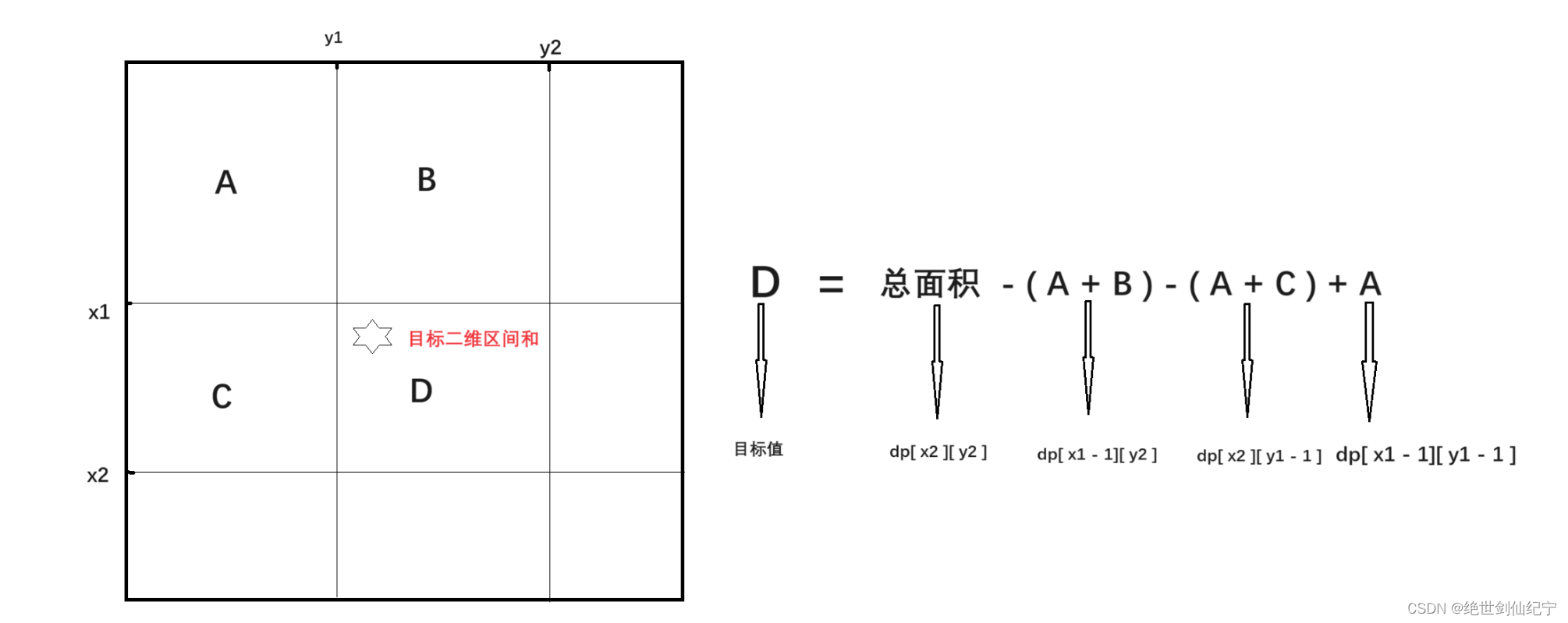
通常用分治法解决一维问题时，我们将一维数轴划分为数段，解决二维问题时就需要把二维空间均匀分成四块，对每一块继续递归。

对于这个问题，我们将棋盘划分为左上、右上、左下、右下四部分，对于每一部分判断特殊方格是否在其中。若特殊方格在这部分棋盘中，就直接将其继续作为一个子问题递归解决；若不在，则填充一个特殊方格，将其改变成一个更小的特殊棋盘（子问题），依次递归解决。按照这样来算，对于当前的整个棋盘的四部分来说，有特殊方格那部分不用覆盖，而其余三部分都新增了一个特殊方格，恰好凑成一个L型骨牌，递归直到当前棋盘只有一个方格为止。如下所示：

算法实现

#include <bits/stdc++.h>
using namespace std;
static int n, g[100][100], num = 1;

void chessBoard(int x, int y, int sx, int sy, int size) {
	if (size == 1)
		return;
	int s = size / 2, t = num++;
	if (sx < x + s && sy < y + s)  chessBoard(x, y, sx, sy, s);//特殊方格在左上角
	else {//特殊方格不在左上角
		g[x + s - 1][y + s-1] = t;//左上角棋盘的右下角
		chessBoard(x, y, x + s - 1, y + s - 1, s);
	}
	if (sx < x + s && sy >= y + s)  chessBoard(x, y + s, sx, sy, s);//特殊方格在右上角
	else {  //特殊方格不在右上角
		g[x + s - 1][y + s] = t;//右上角棋盘的左下角
		chessBoard(x, y + s, x + s - 1, y + s, s);
	}
	if (sx >= x + s && sy >= y + s)  chessBoard(x + s, y + s, sx, sy, s);//特殊方格在右下角
	else {  //特殊方格不在右下角
		g[x + s][y + s] = t;//右下角棋盘的左上角
		chessBoard(x + s, y + s, x + s, y + s, s);
	}
	if (sx >= x + s && sy < y + s)  chessBoard(x + s, y, sx, sy, s);//特殊方格在左下角
	else {  //特殊方格不在左下角
		g[x + s][y + s-1] = t;//左下角棋盘的右上角
		chessBoard(x + s, y, x + s, y + s-1, s);
	}
}

void main() {
	int x, y;//特殊方格坐标
	cin >> n;
	cin >> x >> y;
	g[x][y] = num;
	chessBoard(0, 0, x, y, n);
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++)
			cout << g[i][j] << "\t";
		cout << endl;
	}
}

参考资料

【算法】棋盘覆盖详解，基础教程~