哈喽大家好，今天来给大家带来每日一道算法题系列第三天，让我们来看看今天的题目，一起备战蓝桥杯

题目：

小 Y的桌子上放着 n 个苹果从左到右排成一列，编号为从 11 到 n。

小苞是小 Y 的好朋友，每天她都会从中拿走一些苹果。

每天在拿的时候，小苞都是从左侧第 11 个苹果开始、每隔 22 个苹果拿走 11 个苹果。

随后小苞会将剩下的苹果按原先的顺序重新排成一列。

小苞想知道，多少天能拿完所有的苹果，而编号为 n 的苹果是在第几天被拿走的？

输入格式

输入的第一行包含一个正整数 n，表示苹果的总数。

输出格式

输出一行包含两个正整数，两个整数之间由一个空格隔开，分别表示小苞拿走所有苹果所需的天数以及拿走编号为 n 的苹果是在第几天。

数据范围

对于所有测试数据有：1≤n≤10^9

解题思路：

1 2 3 4 5 6 7 8

题里说每隔着两个苹果拿走一个，所以这段数字的变化规律就是：

2 3 5 6 8

3 5 8

5 8

5

8

首先观察这个题的数据范围，10的九次方，所以我们不能一一个一个的枚举每次拿的苹果，但我们可以一天一天的枚举

怎么样的一天一天的枚举呢，比如说我们现在有n个苹果，每天可以进行隔一个拿一个的操作，那么模拟下来我们每天大约拿三分之一的苹果，也就是三分之n（n/3）每隔两个苹果拿一个苹果，就是（n+2）/3的上取整，什么是上取整：

上取整：

关于上取整，我们可以通过一个函数来了解：

ceil函数：

功能：把一个小数向上取整
      即就是如果数是2.2 ，那向上取整的结果就为3.000000
原型：double ceil(doube x);
    参数解释：
        x:是需要计算的数
返回值：
    成功：返回一个double类型的数，此数默认有6位小数
    无失败的返回值
头文件：#include<cmath>

使用示范：

#include <iostream>
#include <cmath>

int main() {
	double i = ceil(2.2);
	double j = ceil(-2.2);
	printf("The ceil of 2.2 is %f\n", i);
	printf("The ceil of 2.2 is %f\n", j);
	system("pause");
	return 0;
}

 运行截图：

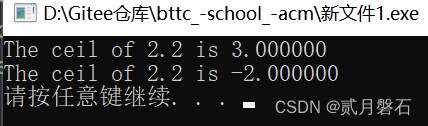
好的，现在什么是上取整都明白了，解题思路也十分清晰，上代码实操吧！！！

解题代码：

#include <iostream>
#include <cmath>
using namespace std;

int main() {
	int n;
	cin >> n;
	int cnt = 0, data = 0;
	while (n) {

		cnt++;
		if (!data && n % 3 == 1)
			data = cnt;
		n -= ceil((n + 2) / 3);
	}
	cout << data << " " << cnt;
	return 0;
}

代码就是根据思路写的，大家如果还有什么不明白的，就在评论里指出吧

觉得有帮助的同学点点关注吧，跟着作者一起备战蓝桥杯，拿下该死的奖！！！

明天见