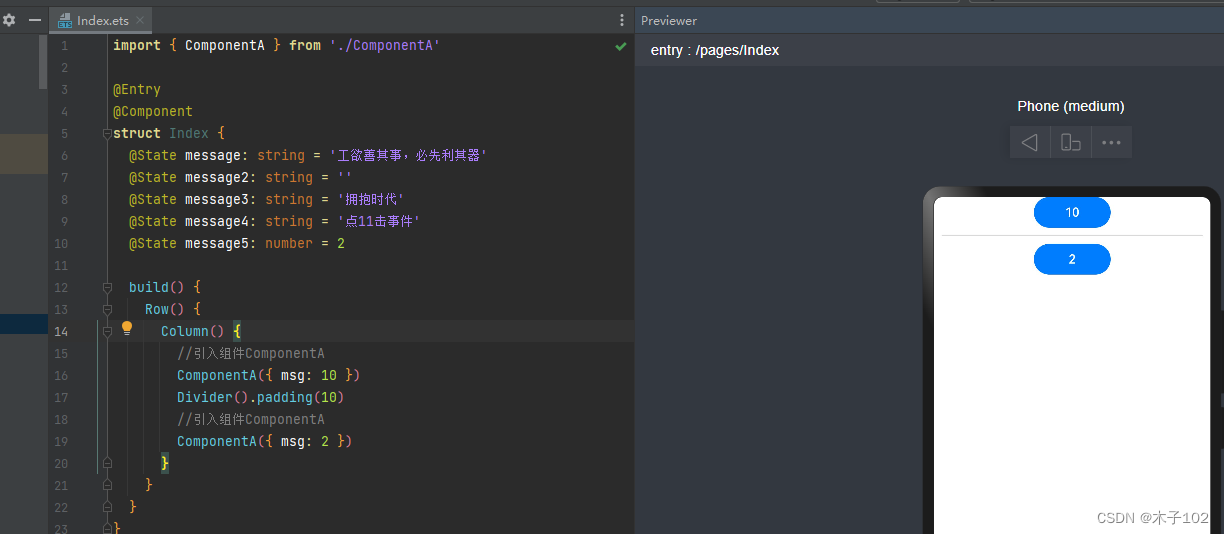
混淆矩阵

其中关于 TP, TN; FP, FN 的解释；

其中首字母 T，F代表预测的情况，即T代表预测的结果是对的， F代表预测的结果是错误的；
第二个字母代表预测是预测为 正样本，还是负样本， Positve 代表正样本;

注意，
此时这里的正样本代表的 是 预测属于某一类别的样本；
负样本则代表预测不属于某一类别的样本。

举例说来

• TP: True 模型预测正确， 预测为正样本Positive;
• FN: False 模型预测错误， 预测为负样本 Negative;

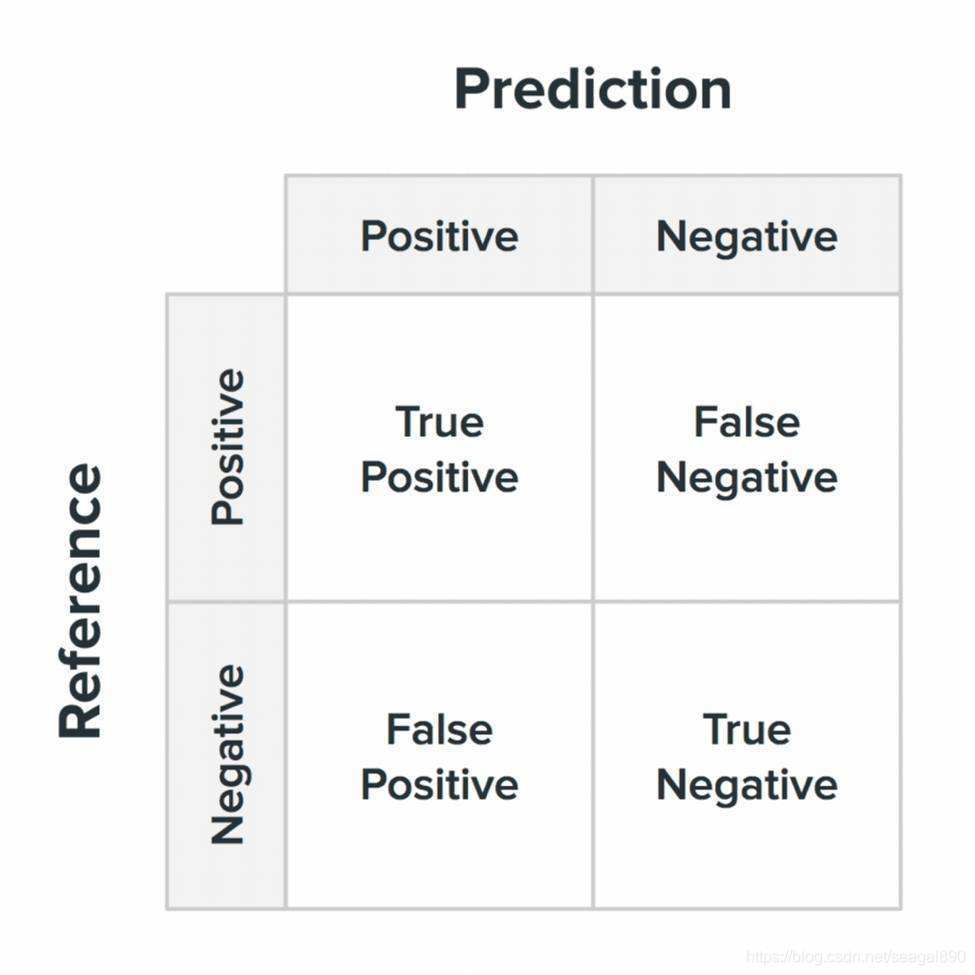
通常情况下，混淆矩阵中， 行代表真实值，列代表预测值，

部分仓库， 与此不一致，列代表真实值，行代表预测值，
需要阅读代码的时候，通过查看文档确定；

1. 基础指标

1.1 准确率 （accuracy）

准确率：衡量正确预测的样本占总样本的比例。这是最简单的指标，

计算方式为 ：
$$\frac{预测正确的样本数目}{所有预测的样本数目}$$

然而，普通的准确率并不适合不平衡的数据集。

• 因为在 类别不均衡的数据集中，
  假设异常类别的样本数目特别多, 异常类别的样本数目很少。

此时， 正常样本的预测正确的个数很高， 但是异常类别的样本全部预测错误，
此时，在这种情况下， 整体样本的准确率仍然非常高， 然而实际情况却并非如此，因为此时异常样本的预测的准确率几乎为0；

1.2 精确率（查准率） Precision

查准率：
它衡量 正确预测的正观测值与预测的正观测值总数的比率。

• 它评估模型预测正类的准确性，计算公式为:

$$\frac{TruePositive}{TruePositive+FalsePositive}$$

分子： True Positive: 预测正确，且预测为正样本， 即混淆矩阵中对角线上的值；
分母： False Positive: 预测错误， 且预测为正样本；

1.3召回率（查全率） Recall ( Sensitivity)

召回率（灵敏度）：它衡量正确预测的阳性观察结果与所有实际阳性结果的比率。

• 它评估模型检测所有正实例的能力，

计算公式为
True Positives
True Positives + False Negatives
True Positives + False Negatives
True Positives
​

分子： True Positive: 预测正确，且预测为正样本， 即混淆矩阵中对角线上的值；
分母： False Negative : 预测错误， 且预测为正样本； 该类别下所有的样本个数， 通常是某一行的所有样本的总和。

1.4 F1值、

F1 分数：精确率和召回率的调和平均值。

• F1 分数在精确度和召回率之间提供了平衡，对这两个指标给予相同的权重。
  其计算方式为

1.5 ROC曲线的AUC值

AUC-ROC (Area Under the Receiver Operating Characteristic Curve)

ROC 曲线是各种阈值的真阳性率（召回率）与假阳性率（1 - 特异性）的图形表示。 AUC-ROC 测量该曲线下的面积，并提供所有可能的分类阈值的总体性能测量

上述指标中，在 Python 中使用 scikit-learn，这些指标可以计算如下：

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_auc_score

# Assuming y_true contains true labels and y_pred contains predicted labels
# Calculate different evaluation metrics
accuracy = accuracy_score(y_true, y_pred)
precision = precision_score(y_true, y_pred)
recall = recall_score(y_true, y_pred)
f1 = f1_score(y_true, y_pred)
auc_roc = roc_auc_score(y_true, y_scores)  # y_scores are the predicted scores or probabilities

# Print the calculated metrics
print(f"Accuracy: {accuracy}")
print(f"Precision: {precision}")
print(f"Recall: {recall}")
print(f"F1 Score: {f1}")
print(f"AUC-ROC: {auc_roc}")

1.6 average 参数的选择

对于 precision_score 、 recall_score 和 f1_score ， average 参数指定对每类指标执行平均的类型，以计算总体指标：

• average=‘micro’ ：
  通过计算所有类别的真阳性、假阴性和假阳性总数来全局计算指标。然后使用这些聚合值计算指标。

• average=‘macro’: 单独计算每个类的指标，然后取这些指标的未加权平均值。平等对待所有类别，无论类别是否不平衡。

• average=‘weighted’ ：单独计算每个类的指标，然后取这些指标的加权平均值，其中每个类的分数按其支持度（真实实例的数量）进行加权。

from  sklearn.metrics import precision_score, recall_score, f1_score

# Assuming y_true contains true labels and y_pred contains predicted labels for multi-class classification
# Calculate precision, recall, and F1-score with different averaging methods
precision_micro = precision_score(y_true, y_pred, average='micro')
precision_macro = precision_score(y_true, y_pred, average='macro')
precision_weighted = precision_score(y_true, y_pred, average='weighted')

recall_micro = recall_score(y_true, y_pred, average='micro')
recall_macro = recall_score(y_true, y_pred, average='macro')
recall_weighted = recall_score(y_true, y_pred, average='weighted')

f1_micro = f1_score(y_true, y_pred, average='micro')
f1_macro = f1_score(y_true, y_pred, average='macro')
f1_weighted = f1_score(y_true, y_pred, average='weighted')

# Print the calculated metrics
print(f"Precision - Micro: {precision_micro}, Macro: {precision_macro}, Weighted: {precision_weighted}")
print(f"Recall - Micro: {recall_micro}, Macro: {recall_macro}, Weighted: {recall_weighted}")
print(f"F1 Score - Micro: {f1_micro}, Macro: {f1_macro}, Weighted: {f1_weighted}")

reference

https://www.cnblogs.com/Yanjy-OnlyOne/p/11362315.html#:~:text=3%E3%80%81%E6%B7%B7%E6%B7%86%E7%9F%A9%E9%98%B5(Confusion%20Matrix,%E4%BB%A3%E8%A1%A8%E7%9A%84%E6%98%AF%E9%A2%84%E6%B5%8B%E5%80%BC%E3%80%82