【LetMeFly】2397.被列覆盖的最多行数：二进制枚举

力扣题目链接：https://leetcode.cn/problems/maximum-rows-covered-by-columns/

给你一个下标从 0 开始的 m x n 二进制矩阵 mat 和一个整数 cols ，表示你需要选出的列数。

如果一行中，所有的 1 都被你选中的列所覆盖，那么我们称这一行 被覆盖 了。

请你返回在选择 cols 列的情况下，被覆盖 的行数 最大 为多少。

 

示例 1：

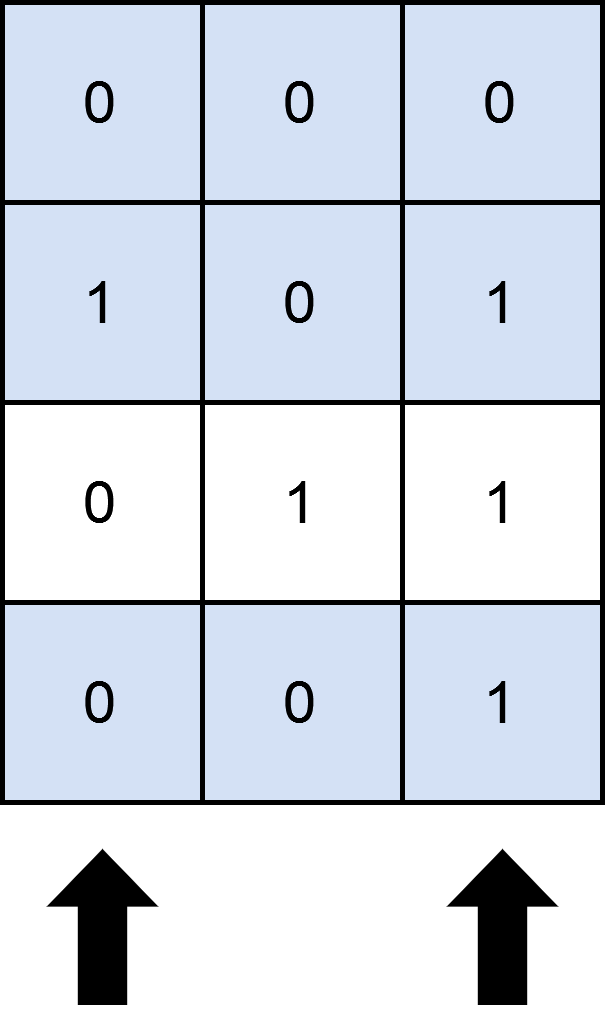
输入：mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出：3
解释：
如上图所示，覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出，不存在大于 3 行被覆盖的方案，所以我们返回 3 。

示例 2：

输入：mat = [[1],[0]], cols = 1
输出：2
解释：
选择唯一的一列，两行都被覆盖了，原因是整个矩阵都被覆盖了。
所以我们返回 2 。

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 12
• mat[i][j] 要么是 0 要么是 1 。
• 1 <= cols <= n

方法一：二进制枚举

使用二进制枚举每一列“选中与不选”的情况。对于某种选择情况：

首先选择的列的要总数为numSelect。接下来开始遍历每一行。对于某一行：

遍历这一行的每一个元素。如果矩阵中这个元素为1但是没有选择这一行，则此行无效。否则遍历完成时此行累加。

累加合法的行，即为“选择”下的结果。

所有合法选择中的最大结果即为答案。

• 时间复杂度$O(2^n\times mn)$，其中$matrix$有$m$行$n$列
• 空间复杂度$O(1)$

AC代码

C++

class Solution {
public:
    int maximumRows(vector<vector<int>>& matrix, int numSelect) {
        int ans = 0;
        int m = matrix.size(), n = matrix[0].size();
        for (int state = 0; state < (1 << n); state++) {
            if (__builtin_popcount(state) != numSelect) {
                continue;
            }
            int thisAns = 0;
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (matrix[i][j] && !(state & (1 << j))) {
                        goto loop;
                    }
                }
                thisAns++;
                loop:;
            }
            ans = max(ans, thisAns);
        }
        return ans;
    }
};

Python

# from typing import List

class Solution:
    def maximumRows(self, matrix: List[List[int]], numSelect: int) -> int:
        ans = 0
        m, n = len(matrix), len(matrix[0])
        for state in range(1 << n):
            if bin(state).count('1') != numSelect:
                continue
            thisAns = 0
            for i in range(m):
                can = True
                for j in range(n):
                    if matrix[i][j] and not state & (1 << j):
                        can = False
                        break
                thisAns += can
            ans = max(ans, thisAns)
        return ans

同步发文于CSDN，原创不易，转载经作者同意后请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/135396524