这道题挺基础但是挺多坑的。(•́へ•́╬)

题目

204. 计数质数 - 力扣（LeetCode）

给定整数 n ，返回 所有小于非负整数 n 的质数的数量 。

示例 

示例 1：

输入：n = 10
输出：4
解释：小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：0

提示：

注意这玩意儿，好东西

• 0 <= n <= 5 * 

 

---

Java解不出来法：普通暴力枚举

emmm，挨个找，挨个判断是吧，应该就可以得出答案

但是如果你写下了如下的代码，就会发现超时啦@!

class Solution {
    public int countPrimes(int n) {
        int res = 0;
        for (int i = 2; i < n; i++) {
            boolean flag = true;
            for (int j = 2; j < n + 1 / 2; j++) {
                if (flag && i != j && i % j == 0){
                    flag = false;
                }
            }
            if (flag){
                res++;
            }
        }
        return res;
    }
}

 

然后冥思苦想得出了如下的枚举优化 

class Solution {
    public static int countPrimes(int n) {
        int count = 0;
        for (int i = 2; i < n; i++) {
            boolean sign = true;
            for (int j = 2; j <  i + 1 / 2; j++) {
                if (i % j == 0) {
                    sign = false;
                    break;
                }
            }
            if (sign){
                count++;
            }
        }
        return count;
    }
}

这里用了break跳过了那么多次循环，甚至第二个循环从 n + 1 / 2 优化到了 i+ 1 / 2，哇，无懈可击对吧！！！我也觉得

送给你

来说题目里 n 的规模达到 及以上时，需要实现的程序的时间复杂度 最高 只能是 O（)的。但还有是有个别“恶心”的题目是,比如这道题^_^; : (

发现并不简单

6666666666666666666666666666666666666666666666

玩啥啊这还

搞不了

官方题解

class Solution {
    public int countPrimes(int n) {
        int ans = 0;
        for (int i = 2; i < n; ++i) {
            ans += isPrime(i) ? 1 : 0;
        }
        return ans;
    }

    public boolean isPrime(int x) {
        for (int i = 2; i * i <= x; ++i) {
            if (x % i == 0) {
                return false;
            }
        }
        return true;
    }
}

不是兄弟我用官方题解还治不了你》？？？？？？？？？？？？？？？？？

搞笑

？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？？

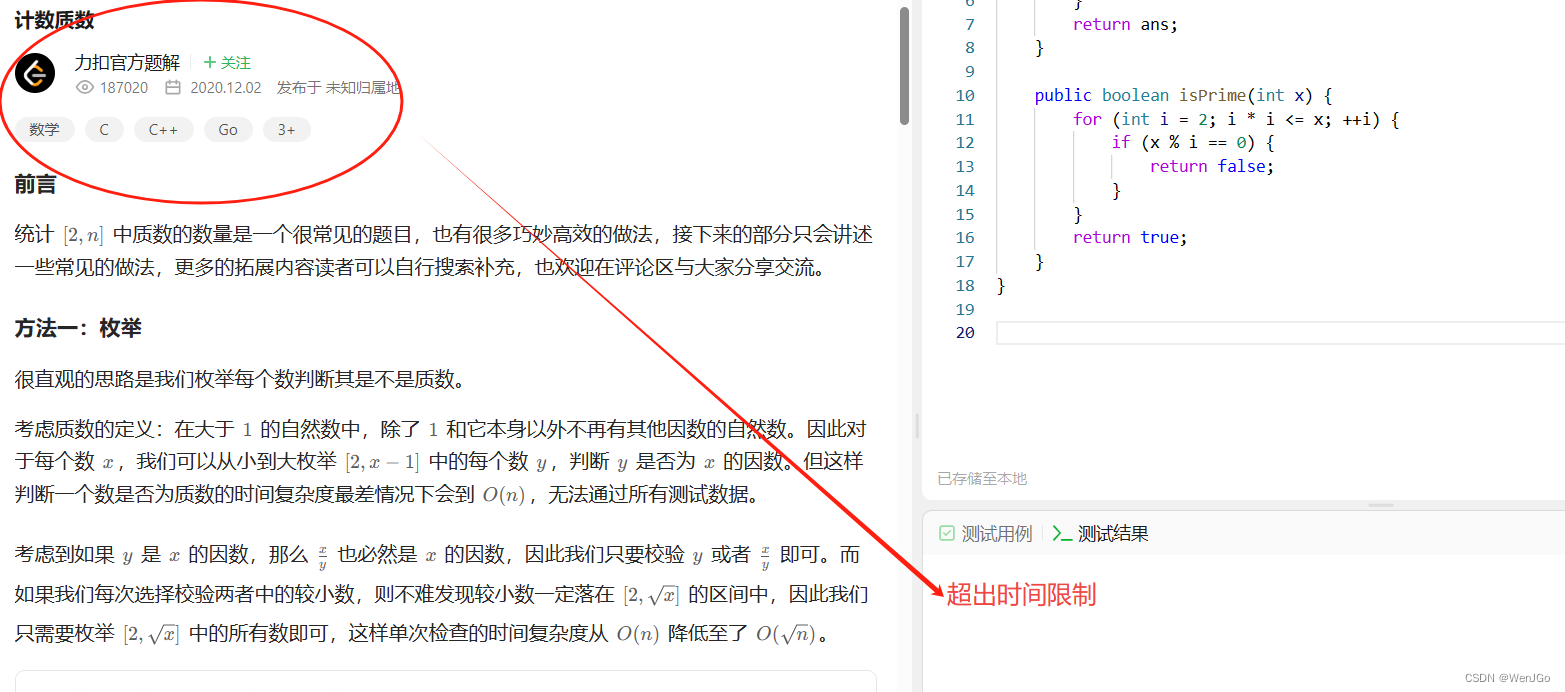
我服

然后就裂开了

然后我就疯狂查资料啊老铁

然后让我发现了一个好东西

埃拉托斯特尼筛法

素数就是质数

维基百科的解释是：

考虑这样一件事情：对于任意一个大于  的正整数 ，那么它的  倍就是合数（）。利用这个结论，我们可以避免很多次不必要的检测。

如果我们从小到大考虑每个数，然后同时把当前这个数的所有（比自己大的）倍数记为合数，那么运行结束的时候没有被标记的数就是素数了。

也就是：

看下面维基百科的动画：

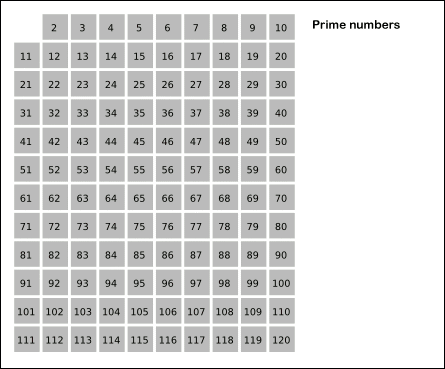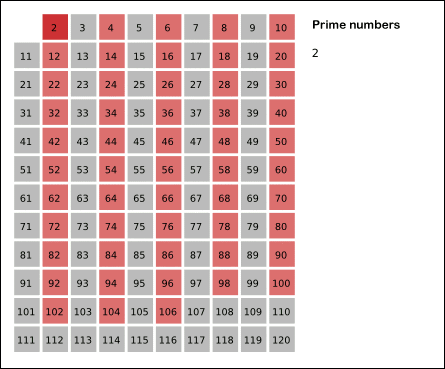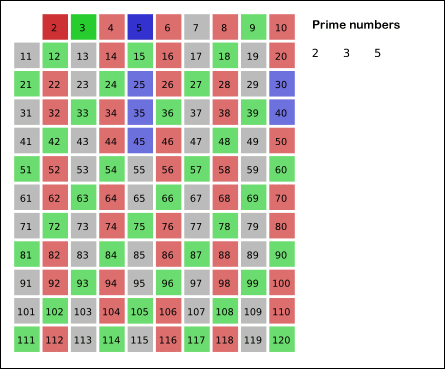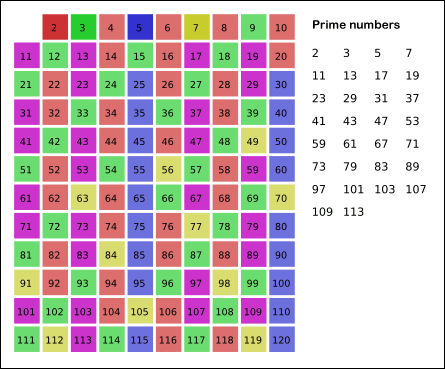
注意每次找当前素数 x 的倍数时，是从 开始的。因为如果 x>2，那么 2 * x 肯定被 2 给判断过一次了，最小未被过滤的肯定是 .

哈哈哈哈哈哈哈哈

class Solution {
    public int countPrimes(int n) {
        if (n <= 2) {
            return 0;
        }
        boolean[] isPrime = new boolean[n];
        // 初始化所有数为质数
        for (int i = 2; i < n; i++) {
            isPrime[i] = true;
        }
        // 埃拉托斯特尼筛法
        for (int i = 2; i * i < n; i++) {
            if (isPrime[i]) {
                for (int j = i * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        // 统计质数的数量
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                count++;
            }
        }
        return count;
    }
}

现在肯定跑的出来了吧，哈哈哈哈哈哈哈哈哈哈哈哈

总结

下次写题先看官方题解谢谢