一、对撞指针

        对撞指针由两个指针组成，分别指向数据的头部和尾部：

        两个指针分别从两头移动，寻找符合答案的位置后停下。对撞指针主要应用于有序数组的求和，我们使用一个题目进行说明：

         示例如下：

         根据题目可以得出以下条件：

• 数组是按照有序递增的顺序排列的。
• 不可以使用重复相同的元素（即index1=index2不合理），而是存在1<index1<index2<=numbers.Length的关系。
• 只对应唯一的答案，也就是答案可能不止一个，只需要输出其中一个即可

        解决方案有很多，使用两个for进行遍历、二分查找、动态规划等等，我们使用示例一来讲解对撞指针：

         初始化两个头尾指针，分别指向数组的头尾部分：

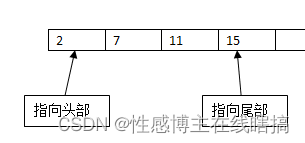
         判断一下当前数值相加是否符合目标数，2 + 15 = 17 > 9 ，尾部指针向左移动：

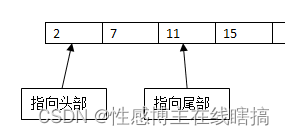
        再来判断一下：2 + 11 = 13 > 9，继续尾部指针向左移动：

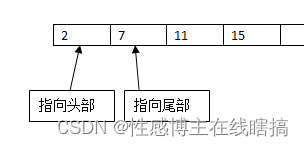
        2 + 7 = 9 == 9，输出结果。看到这里，估计很多人会一脸懵，为什么这样就可以得出正确结果？ 下面我们使用一个例子来分析说明：

         我们把所有可能的相加结果都列举出来：

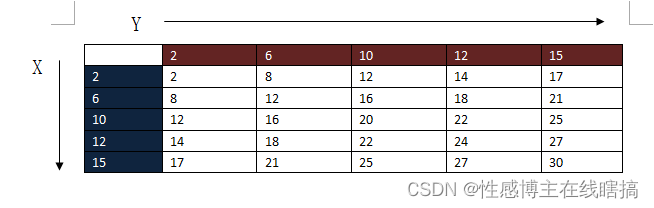
         根据条件二，我们首先排除index1 = index 2的情况：

         黑色部分为淘汰部分：

        紧接着淘汰index1 > index2部分：

 

        当前头尾指针所指向的数值之和为17，使用橙色标记：

 

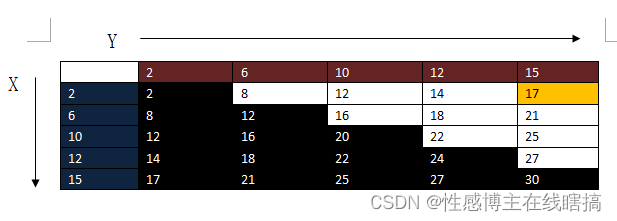
        2+15 = 17 < 22，说明两数之和应该还要往上增加，而此时尾指针所指向的数已经是最大了，所以需要让头指针往右移动才可以使得两数之和往上增加，继而推断出头指针所指向的“2” 与尾指针指向的“6、10、12、15”都不符合，因为“15”已经是最大都不符合目标数，其他比它小的数就更不用说，当前头指针往右移动：

         当前情况如下：

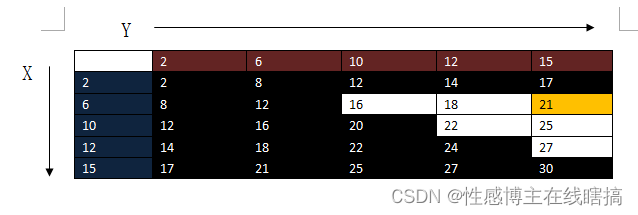
         紧接着再来推断，6 + 15 = 21 < 22，说明两数之和还不够大，继续往上增，头指针再往右移动：

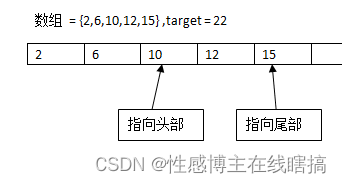
        按照上面说的再次排除一项：

        10 + 15 = 25 > 22，只要看明白上面说的原理，这里理解起来也很简单，就是两数之和比目标数要大，所以要让两数之和减少，因为头指针所指向的数已经是最小的了，所以需要让尾指针往左移动来减少两数之和：

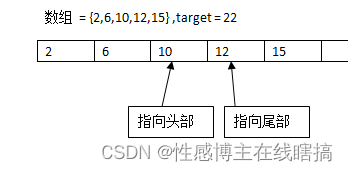
         将Y中的一项排除掉：

        最后剩下的那个数，即为正确答案，由此我们可以得出对撞指针的判断条件：

• 两数之和大于目标数，尾指针往左移动
• 两数之和小于目标数，头指针往右移动
• 两数之和等于目标数，输出结果

        对撞实现的代码如下（参考）：

        下一章将介绍快慢指针，用于快速求取中间数。