目录
今日知识点:
使用并查集映射点,构造迷宫的连通块
vis计时数组要同步当回合的处理
递归求先序排列
基于不相邻的取数问题:dfs+回溯
n个相同球放入k个相同盒子:dfs的优化分支暴力
01迷宫
血色先锋队
求先序排列
取数游戏
数的划分
01迷宫


思路1:
其实啊:在写这个题的时候,总觉得这个题没法做,感觉时间复杂度非常高。因为一共(n*m)^4,一共这么格子,然后每个格子有4种选择…………
然后我犯了一个错误,其实dfs的复杂度不是这么看的,因为其实很多分支根本就没走。远远达不到那种耗时。就比如说正常的走迷宫问题,设置一个vis数组,然后dfs的复杂度最大也就整张地图罢了,根本不会达到每个点都做那么多个分支的情况数。所以哈。dfs的实际复杂度还得看实际的效果!扯远了………………
设置dfs(int x,int y,int z,int t)进行四个方向的暴搜就行,因为最多也就是搜1000次,然后本次搜索过的之后就不需要再搜索了,完全不会超时。
#include <bits/stdc++.h>
using namespace std;
char s[1005][1005];
int n,m,ans[100005],f[1005][1005];
void dfs(int x,int y,int z,int t){
if(x<0||y<0||x>=n||y>=n||f[x][y]!=-1||s[x][y]-'0'!=z)return ;
ans[t]++;f[x][y]=t;
dfs(x-1,y,!z,t);
dfs(x,y-1,!z,t);
dfs(x+1,y,!z,t);
dfs(x,y+1,!z,t);
}
int main(){
cin>>n>>m;int x,y;
memset(f,-1,sizeof(f));
for(int i=0;i<n;i++)
cin>>s[i];
for(int i=0;i<m;i++){
scanf("%d%d",&x,&y);x--;y--;
if(f[x][y]==-1){
dfs(x,y,s[x][y]-'0',i);
}
else{
ans[i]=ans[f[x][y]];
}
}
for(int i=0;i<m;i++)
printf("%d\n",ans[i]);
}其实你也看到了, 就是一道连通块的题,扫一下每个连通块内有多少个块罢了。
思路2:
既然都是连通块的题了,并查集做才最合理!
操作就是不断的去合并两个点,合并点的话需要进行映射(说白了就是找一个东西来唯一的表示这个点)最直接做法的就是映射成一维。最后合并的时候一边维护fa一边维护cnt就行了。
注意:千万不能从(0,0)开始,不然会映射失败。
#include <bits/stdc++.h>
using namespace std;
string s[1005];
int n,m;
int dx[]={0,-1,0,1},dy[]={1,0,-1,0};
int fa[1005*1005],cnt[1005*1005];
int real (int i,int j){return (i-1)*n+j;}
int find(int x){
if(x!=fa[x])fa[x]=find(fa[x]);
return fa[x];
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++)
cin>>s[i],s[i]="0"+s[i];
int x,y,f1,f2;
for(int i=1;i<=n*n;i++)fa[i]=i,cnt[i]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=0;k<4;k++){
x=i+dx[k];y=j+dy[k];
if(x>=1&&y>=1&&x<=n&&y<=n&&s[x][y]!=s[i][j]){
f1=find(real(i,j));
f2=find(real(x,y));
if(f1!=f2){
fa[f2]=f1;
cnt[f1]+=cnt[f2];
}
}
}
while(m--){
scanf("%d%d",&x,&y);
printf("%d\n",cnt[find(real(x,y))]);
}
}
血色先锋队


思路:
有一种特别直接的做法:其实想找领主的最早感染时候,不过就是直接曼哈顿距离就能求出来了。那么求一个领主需要O(a)时间,找b个领主需要O(a*b)时间,不好意思直接会超时的。
所以这不是最聪明的做法,而是做不好的做法。
虽然说感染源很多,但是我们可以把这个感染源一起进行扩散,然后扩散整个图的时候,所有领主的感染时间也就确定了。仅需要一张图的时间罢了。
这里有个bug改了好久才发现,vis标记一定要同步于当回合处理。
(果然,迷迷糊糊的时候尽量不要敲代码啊)
#include <bits/stdc++.h>
using namespace std;
int a,b,n,m;
int vis[550][550];
struct node{int x;int y;};
int dx[]={1,0,-1,0},dy[]={0,1,0,-1};
int main(){
cin>>n>>m>>a>>b;
int x,y,t=0;
memset(vis,-1,sizeof(vis));
queue<node>q;
for(int i=1;i<=a;i++){
scanf("%d%d",&x,&y);
q.push(node{x,y});
vis[x][y]=t;//入队就标记:一定要当回就标记,避免下回合开始之后上回合还没有标记
}
while(!q.empty()){
int sz=q.size();t++;
while(sz--){
node cur=q.front();q.pop();
for(int i=0;i<4;i++){
int tx=cur.x+dx[i],ty=cur.y+dy[i];
if(tx<1||ty<1||tx>n||ty>m||vis[tx][ty]!=-1)continue;
q.push(node{tx,ty});
vis[tx][ty]=t;//在利用队列中点进行下一层处理时候,当前队列的所有点均已经安全标记
}
}
}
for(int i=1;i<=b;i++){
scanf("%d%d",&x,&y);
printf("%d\n",vis[x][y]);
}
}
求先序排列

思路:
一道dfs题的老朋友了。
直接模拟就行:给个例子:中序ACGDBHZKX,后序CDGAHXKZB
找到主根B,然后左子树(ACGD,CDGA)重复操作,右子树(HZKX,HXKZ)重复操作即可。
然后注意输出是先序,所以先输出根,然后递归左边,最后是右边。
最最后注意结束条件就行了(长度为1就结束,不要进入错误操作)
#include <bits/stdc++.h>
using namespace std;
void dfs(string s1,string s2){
int sz1=s1.size(),sz2=s2.size();
if(sz1==1){
cout<<s1;return ;
}
string s11,s12,s21,s22;
char ch=s2[sz2-1];
int i=s1.find(ch);
s11=s1.substr(0,i);
s12=s1.substr(i+1);
s21=s2.substr(0,i);
s22=s2.substr(i,sz2-i-1);
cout<<ch;
if(s11.size())
dfs(s11,s21);
if(s12.size())
dfs(s12,s22);
}
int main(){
string s1,s2;cin>>s1>>s2;
dfs(s1,s2);
}
取数游戏


思路:
我一开始的思路是dfs(x1,y1,x2,y2)然后转移到下一个(i,j,i+1,j+1)也就是用i+1,j+1来标记走过的状态。嗯~ 后面再一看,我去,这样子只能不与上一个状态冲突,那么和上上个状态就冲突。反正就是必须整个图都要进行标记,我标记的不够。
那么就dfs+回溯,进行全图标记。
首先装模装样的分析一下dfs的时间复杂度:首先基于回溯的话,每个格子妥妥的要跑2种状态。一共36个格子,所以2^36??? 等等,因为是跳着走的,所以因为2^18左右吧(其是不是很会)
#include <bits/stdc++.h>
using namespace std;
const int d[8][2]={1,0,-1,0,0,1,0,-1,1,1,-1,1,1,-1,-1,-1};
int ans,n,m,t;
int vis[8][8],a[8][8];
void dfs(int x,int y,int mx){
if(y==m+1){
dfs(x+1,1,mx);
return ;
}
if(x==n+1){
ans=max(ans,mx);
return ;
}
dfs(x,y+1,mx);
if(vis[x][y]==0){
for(int i=0;i<8;i++){
vis[x+d[i][0]][y+d[i][1]]++;
}
dfs(x,y+1,mx+a[x][y]);
for(int i=0;i<8;i++){
vis[x+d[i][0]][y+d[i][1]]--;
}
}
}
int main(){
cin>>t;
while(t--){
ans=0;
memset(a,0,sizeof(a));
memset(vis,0,sizeof(vis));
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[i][j];
dfs(1,1,0);
cout<<ans<<'\n';
}
}
数的划分
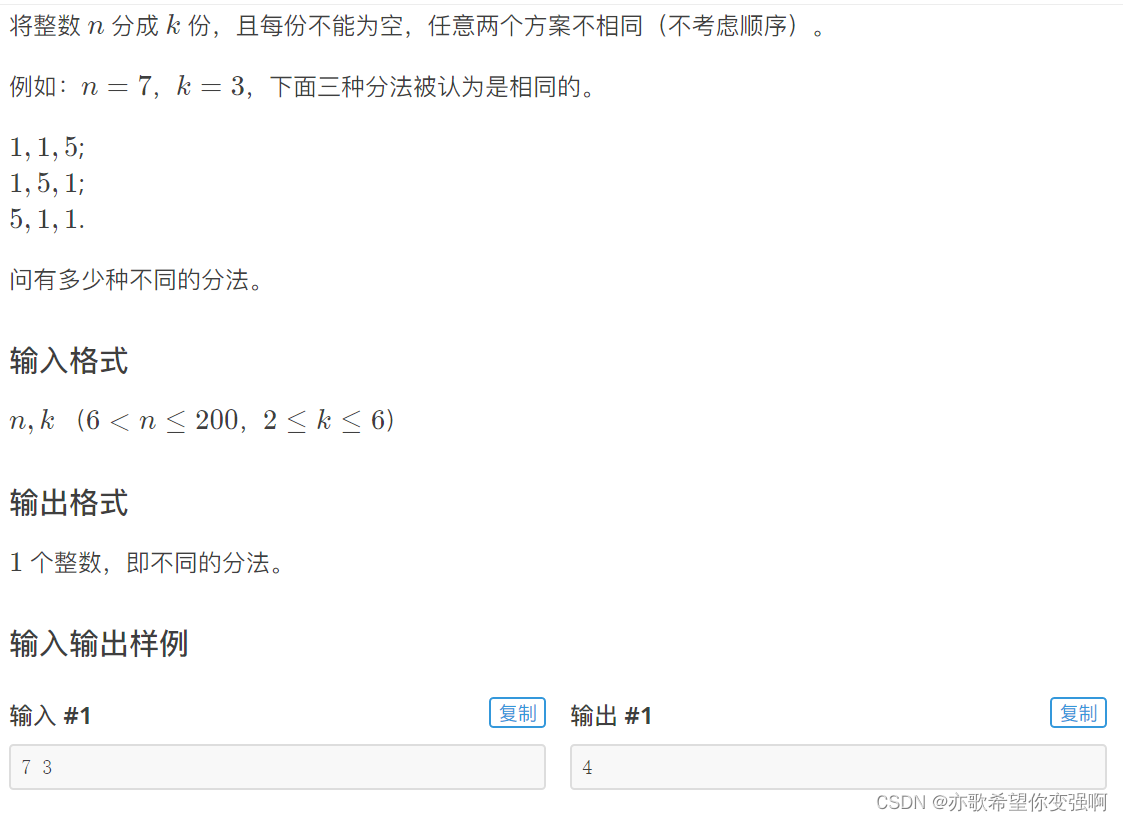

思路:
两种做法:
第一种:动态规划:
题目可以理解成把n个相同球放入k个相同盒子,然后因为球都是相同的,就不能再对最后一个球进行讨论了。应该对应一类球:
设置a[i][j]表示i个球放入j个盒子的方案数。
第一种情况:有一个盒子只有一个球,那么就对应了a[i-1][j]
第二种情况:每个盒子都至少有两个球,那么就对应看a[i-j][j]
所以:a[i][j]=a[i-j][j]+a[i-1][j-1]
第二种:dfs:
在已经放了i时候,每次可以放1~n-i个,所有dfs(i)有n-i个分支,这个复杂度很高,别着急,只需要把无效分支剔除即可很快。
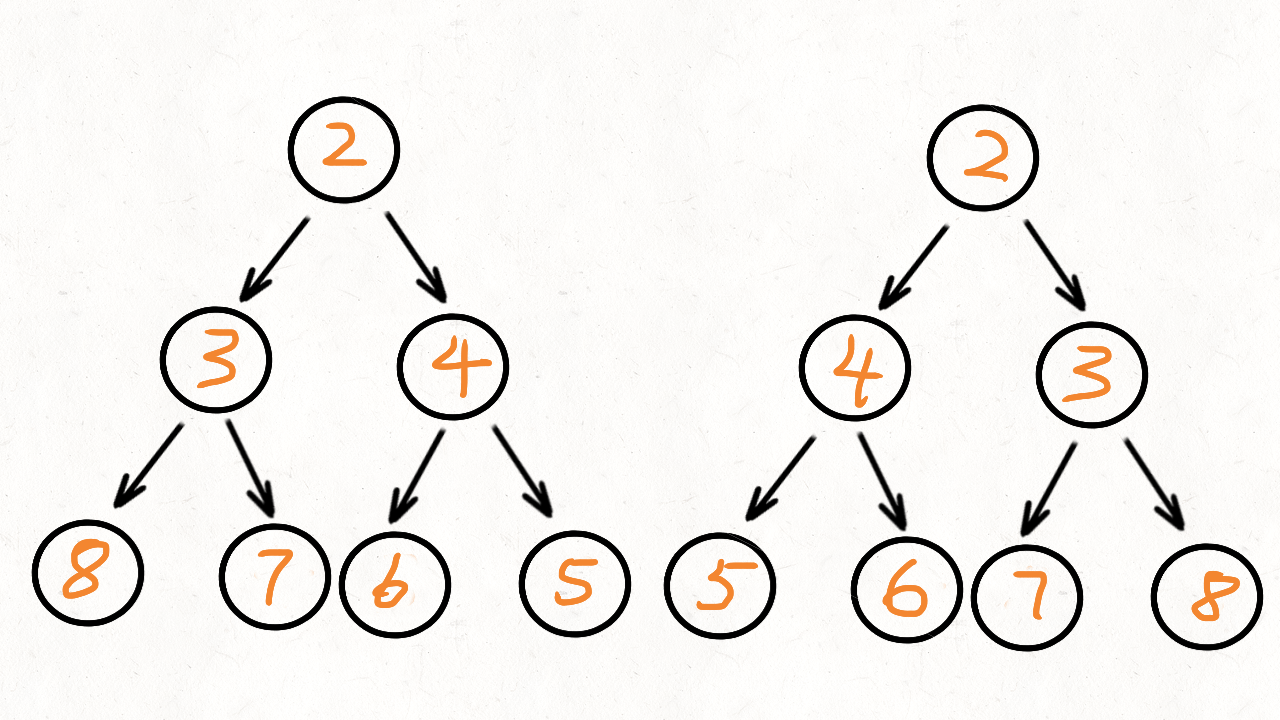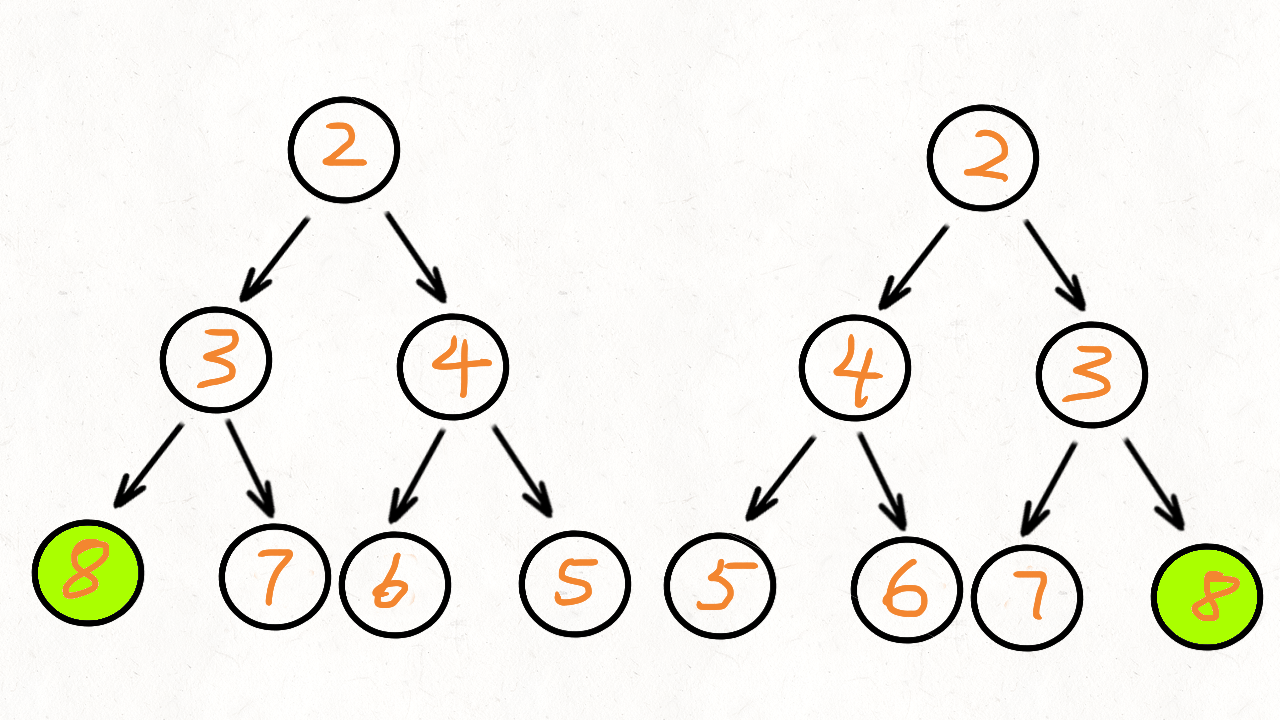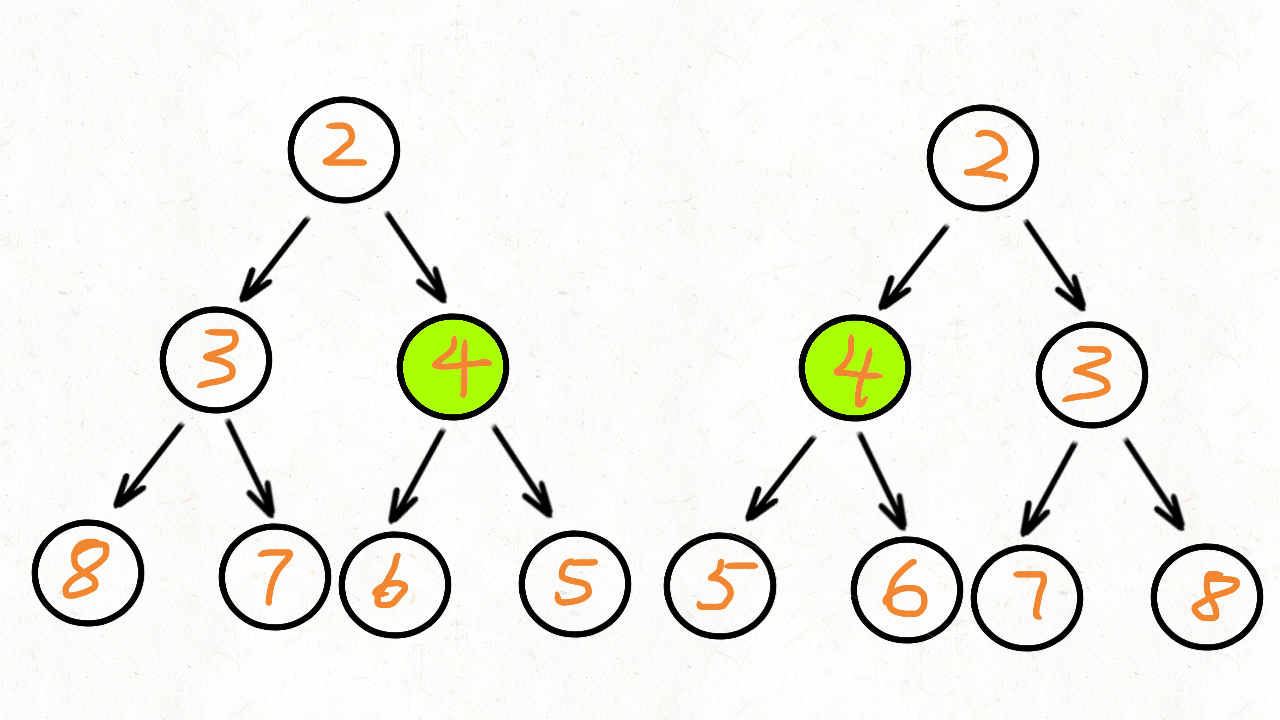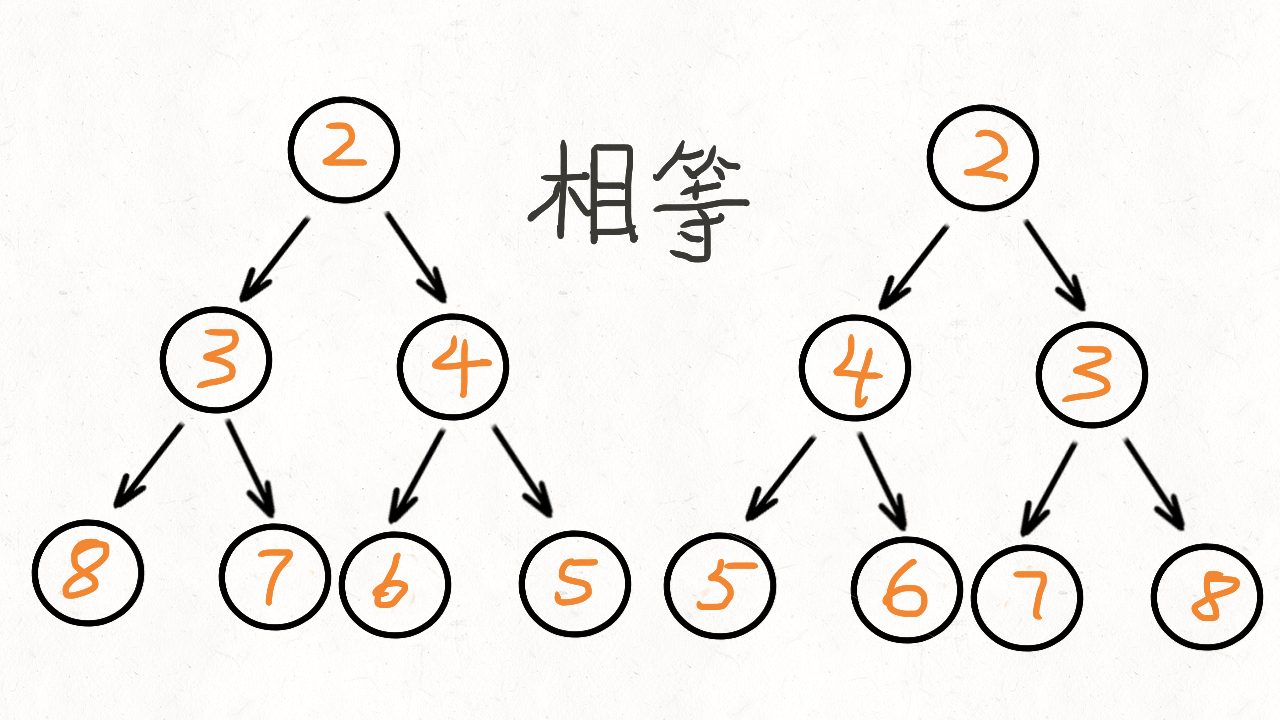
仔细观察7的拆法:
1 1 5
1 2 4
1 3 3
2 2 3
2 3 2(重复了哟)
所以你发现了,要想不重复 ,就必须后面选的数比前面的大,(很早的时候我们再输出组合数的时候就是这样子去重的,只需要安排升序即可),所以在dfs(i)也就是选了i的时候,后面选的数都必须比i大,那么有了sum+i*(k-cnt)<=n这个分支优化。
dfs的速度就变快了很多。
#include <bits/stdc++.h>
using namespace std;
int n,k,ans=0,a[205][70];
//int main(){
// cin>>n>>k;
// for(int i=1;i<=n;i++)a[i][1]=1;
// for(int i=2;i<=n;i++)
// for(int j=2;j<=(i,k);j++){
// a[i][j]=a[i-1][j-1];
// if(i>=2*j)a[i][j]+=a[i-j][j];
// }
// cout<<a[n][k];
//}
void dfs(int cnt,int up,int sum){
if(cnt==k){
if(sum==n)ans++;
return ;
}
for(int i=up;sum+i*(k-cnt)<=n;i++){
dfs(cnt+1,i,sum+i);
}
}
int main(){
cin>>n>>k;
dfs(0,1,0);
cout<<ans;
}![[Android]RadioButton控件](https://img-blog.csdnimg.cn/3327391eaf3b49b58456e262120fcac3.png)