图像识别是计算机视觉领域中的一个重要任务,其目标是使计算机系统能够理解和解释图像中的信息。以下是图像识别的基本原理:
1. 数据采集:首先,需要获取图像数据。这可以通过摄像头、传感器、扫描仪等设备来实现。图像可以是静态的照片,也可以是视频流。
2. 图像预处理:在进行识别之前,通常需要对图像进行一些预处理操作。这可能包括图像的缩放、裁剪、旋转、灰度化等操作,以确保图像数据的一致性和适应性。
3. 特征提取:特征是图像中用于区分和识别对象的关键信息。特征提取阶段涉及识别图像中的重要模式、结构和颜色等特征。常见的特征提取方法包括边缘检测、角点检测、颜色直方图等。
4. 模型训练:利用已标记的图像数据集,训练机器学习模型或深度学习模型。常用的模型包括支持向量机(SVM)、卷积神经网络(CNN)、循环神经网络(RNN)等。模型的训练过程就是学习如何从图像特征中推断出图像中的对象或模式。
5. 模型测试与推断:经过训练的模型可以用于测试和推断。当新的图像输入时,模型会利用之前学到的知识来识别图像中的对象或模式。输出可能是一个类别标签、位置信息等,具体取决于任务的性质。
6. 优化与调整:根据模型的性能和需求,可能需要对模型进行优化和调整,以提高识别准确性、降低误差率等。
7. 应用领域:图像识别广泛应用于人脸识别、物体识别、车牌识别、医学影像分析、无人驾驶、安防监控等众多领域。
总体而言,图像识别的原理涉及数据采集、预处理、特征提取、模型训练和推断等多个步骤,其中机器学习和深度学习技术在图像识别中起着关键作用。
图像识别在数学上涉及多个领域的知识,以下是一些常见的数学概念和公式,它们在图像识别的原理中起到关键作用:
1. 卷积操作(Convolution): 卷积神经网络(CNN)是图像识别中常用的深度学习模型。卷积操作用于提取图像中的特征。其数学表示为:
![]()
其中 \(f\) 和 \(g\) 是两个函数,\(\tau\) 是积分变量,\(*\) 表示卷积操作。
2. 梯度(Gradient): 在边缘检测和特征提取中常用到梯度。梯度表示函数在某一点上的变化率。在图像中,梯度可以用于检测图像中的边缘。
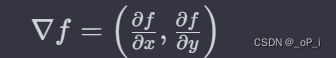
其中 \(\frac{\partial f}{\partial x}\) 和 \(\frac{\partial f}{\partial y}\) 分别表示函数 \(f\) 对 \(x\) 和 \(y\) 的偏导数。
3. 特征空间变换(Feature Space Transformation): 在一些传统的图像处理方法中,特征空间变换用于将图像转换到另一种特征表示,以便更容易进行分类或检测。例如,离散傅里叶变换(DFT):

其中 \(F(u, v)\) 是图像的频谱表示,\(f(x, y)\) 是原始图像的像素值,\(M\) 和 \(N\) 是图像的宽和高。
4. 池化(Pooling): 池化操作用于减小特征图的空间维度,提高计算效率。一种常见的池化操作是最大池化:
![]()
其中 \(\text{pixels}\) 是池化窗口内的像素值。
这些数学概念和公式只是图像识别中涉及的一小部分。在深度学习中,大量的数学知识用于定义神经网络的结构、损失函数、优化算法等。深度学习框架(如TensorFlow、PyTorch)提供了高级的抽象,使得实际应用中对这些数学概念的深入理解不是必需的,但了解这些数学概念可以帮助理解图像识别的基本原理。