前言

经常会有一些算法，我们说常用不常用，说不用也偶尔会用，当时看记住了，过几天提起来又忘记了，这是为什么呢？以博主为例，当时看的时候的确是“记住了”，问题就出在这个“记”上，算法是不能用记忆力去暴力破解的，需要理解，理解了，即使记不住，也可以根据理解手写出来。今天，我将带领大家掌握这些基础算法的要领，让你在需要的时候手写出来，而不是靠记忆背下来。

冒泡排序

原理

相邻元素两两比较，大的/小的往后排，一轮比较结束，最大值出现在最大下标处。会比较n-1轮。

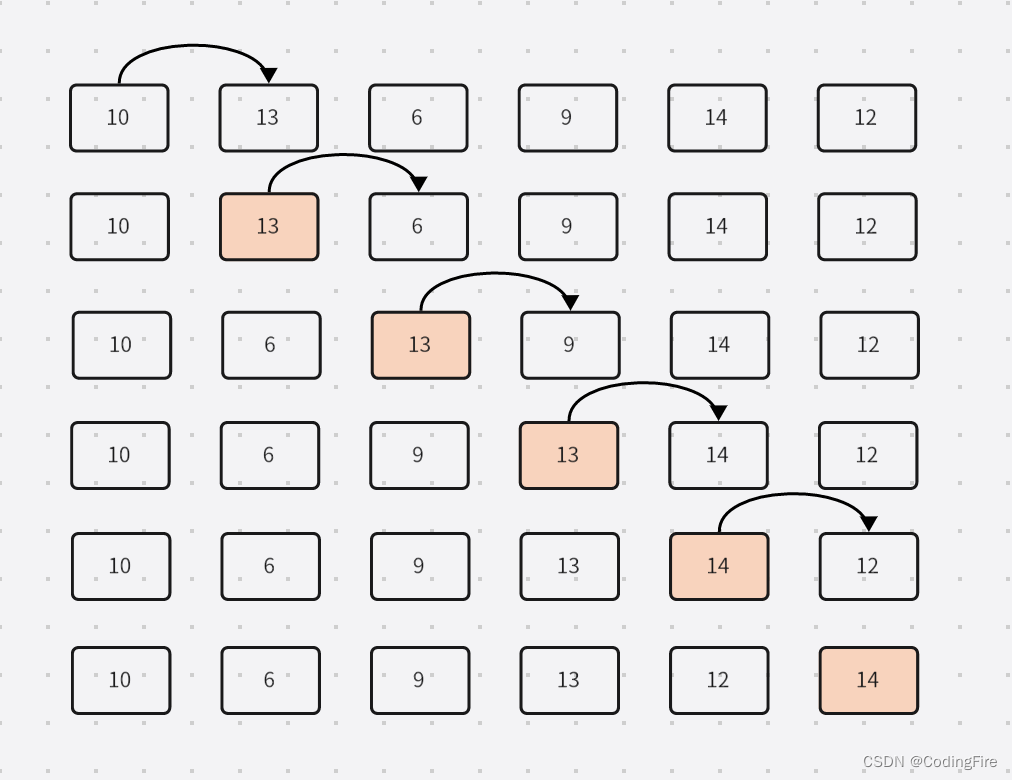
看上图，两两比较，第一轮的最大值就已经排到最右侧了，接着就是第二轮，第三轮，第四轮...并且每一轮开始，都是从第0位开始比较，但从最后一位开始，都会少进行（第N轮）次比较，每一轮的最后一位都是已经排好的。

最终得到的数组如下：[6，9，10，12，13，14 ]。

我们尝试来谢谢冒泡的代码：

int[] ary = {10, 13, 6, 9, 14, 12};
//共比较ary.length-1轮
for (int i = 0; i < ary.length - 1; i++) {
    //每一轮次内的比较又会少相应轮次的比较
    for (int j = 0; j < ary.length - 1 - i; j++) {
        //j > j + 1 进行交换
        if (ary[j] > ary[j + 1]){
            int tmp = ary[j];
            ary[j] = ary[j+1];
            ary[j + 1] = tmp;
        }
    }
}
//最后我们输出看下结果和我们预测的一样不
System.out.println(Arrays.toString(ary));

这样，冒泡排序就写好了，核心要点在排几轮？每一轮最后少排几个？因为越排，尾部排好的顺序就越多，相应的就要减少每一轮内比较的次数，你要是选择每一轮都通排，那也行，只不过效率就降低了，这也就失去了我们用算法的初衷。

选择排序

原理

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。

你听明白了吗？没关系，我们用下图来进行说明：

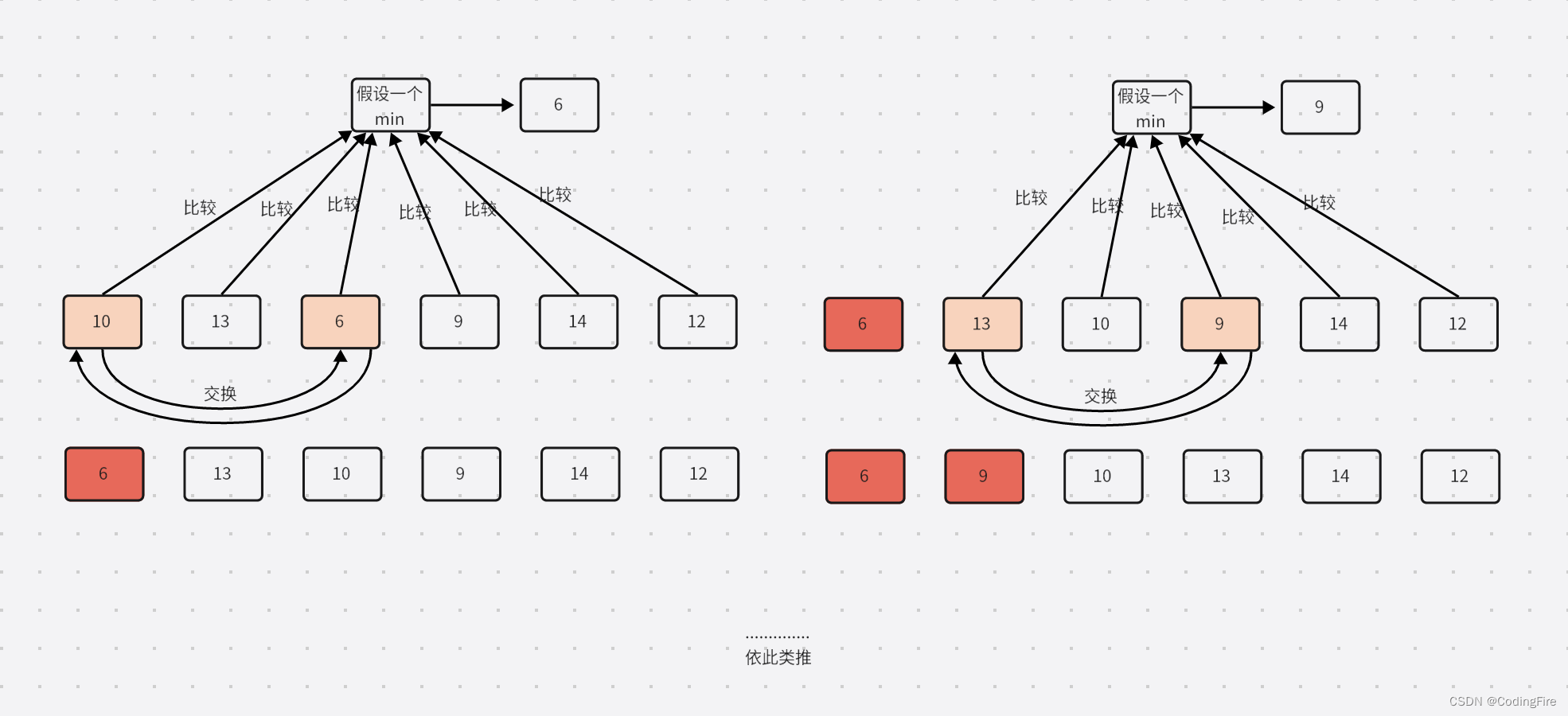
这样，原理就出来了，逻辑也出来了，我们可以尝试着写一写代码了：

int[] ary = {10, 13, 6, 9, 14, 12};
//共比较ary.length-1轮
for (int i = 0; i < ary.length - 1; i++) {
    //假设最小值为i
    int min = i;
    //每一轮前面就会有一个已经排好序的元素，所以我们不能重新对此元素进行排，就需要从i位开始比较
    for (int j = i; j < ary.length; j++) {
        //j > j + 1 进行交换
        if (ary[j] < ary[min]){
            //寻找最小值的下标
            min = j;
        }
    }
    //交换最小值和第i位
    int tmp = ary[i];
    ary[i] = ary[min];
    ary[min] = tmp;
}
//最后我们输出看下结果和我们预测的一样不
System.out.println(Arrays.toString(ary));

n-1轮后，排序就完成了，需要注意的点就在图里，大家也可以尝试着画下接下来的图，相信你很快就能掌握选择排序算法了。

我们上面提到了稳定性，说选择排序是不稳定的排序算法，这是为什么呢？

首先，我们要先知道什么是稳定和不稳定的排序：排序后相同元素的前后相对位置发生改变，就是不稳定的排序，不改变，就是稳定性排序。

举个例子说明：{3，5，6，1，3，7，9}第一次排序，3和1交换位置，两个3的相对位置发生了变化，那么这就是一个不稳定的排序。这个不用纠结原因，规定就是这样，记住就好，只出现在有相同元素的情况下。

插入排序

原理

插入排序也称为直接插入排序，对于少量的元素排序，它是一个有效的算法，它的思想是将一个元素插入已经排好序的有序表中，从而变成一个新的，记录数+1的新有序表。和选择排序类似，也是将元素分为两部分，一个是已经排序的，一个是没有排序的，对未排序的部分进行遍历，将遍历的元素分别插入到已经排好序的队列中的合适位置，直到未排序部分元素数为0。

我们用一张图来表示下：

插入时，我们是从当前位置开始往第0位上倒着比较，小于第几位，就讲遍历的元素插入到第几位的前面。

图也有了，我们仿照着选择排序，可以来写写代码了：

int[] ary = {10, 13, 6, 9, 14, 12};
//共比较ary.length-1轮，这里第0位默认排好序，所以从第1位开始遍历
for (int i = 1; i < ary.length; i++) {
    //这里需要往前找，并比较大小，小的话就插入进去
    for (int j = i; j > 0 && ary[j] < ary[j - 1]; j--) {
        //ary[i] == ary[j],这里依次倒序进行比较，满足条件就进行交换， 
        //直到把arr[j]插入到合适的位置为止
        int tmp = ary[j];
        ary[j] = ary[j - 1];
        ary[j - 1] = tmp;
    }
}
//最后我们输出看下结果和我们预测的一样不
System.out.println(Arrays.toString(ary));

这里的倒序比较很像冒泡，只不过是反向的，且有条件进行约束。需要注意的是第一次的交换10<13，所以位置不需要动，这时候已经排好序的部分就是第0，1位。

二分查找排序

原理

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

前提：

顺序存储结构，比如数组
已经实现了排序

线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。

线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的（注意：这句话只适用大部分线性表，而不是全部。比如，循环链表逻辑层次上也是一种线性表（存储层次上属于链式存储，但是把最后一个数据元素的尾指针指向了首位结点）

顺序存储结构是存储结构类型中的一种，该结构是把逻辑上相邻的结点存储在物理位置上相邻的存储单元中，顺序存储结构的主要优点是节省存储空间。结点之间的逻辑关系由存储单元的邻接关系来体现。

查找过程：假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。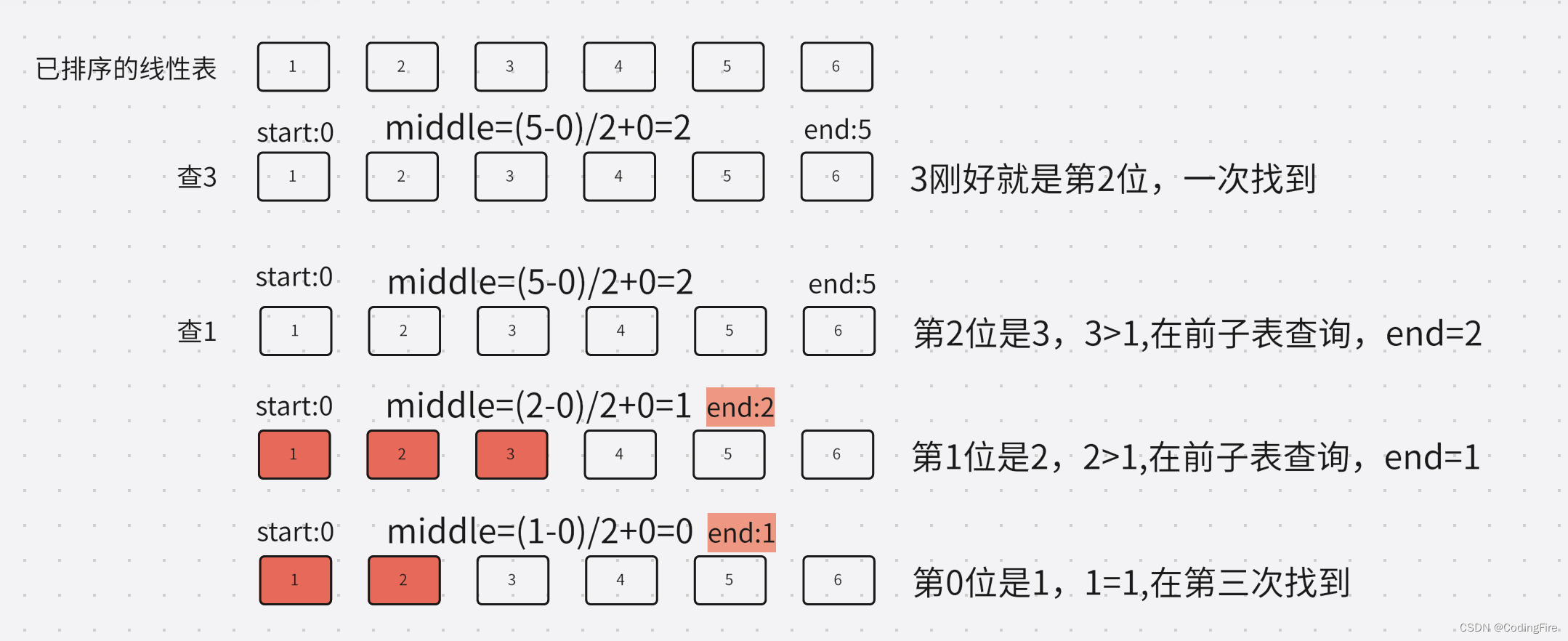

在偶数表中，middle这里采用的是使用前一位的值，其实选后一位的值也是可以的，无需介意。

我们来试着写出代码：

    //根据元素查询对应的下标
    public static int search(int[] ary,int tar){
        int start = 0,end=ary.length - 1,middle;
        while (start<=end){
            //确定中间位置的下标
            middle = (end - start) / 2 + start;
            //比较middle的元素与目标元素是否相等
            if (tar == ary[middle])
                return middle;
            else if(tar > ary[middle])
                //从while处重新开始查找
                end = middle - 1;
            else
                //从while处重新开始查找
                start = middle + 1;
        }
        return -1;
    }

注意：有人在计算middle的时候会采用middle = (start + end) / 2的方式，在数组长度不大的时候，这也是可以的，但是有个问题，如果start和end值过大，就会导致start + end超出作用域，middle就和原值不一样了，为了防止这种情况的出现，采用middle = (end - start) / 2 + start。

为什么要加上start呢？前半部分start=0，加不加都是一样的，查找的部分如果是后半部分，就需要加上start的位置了。