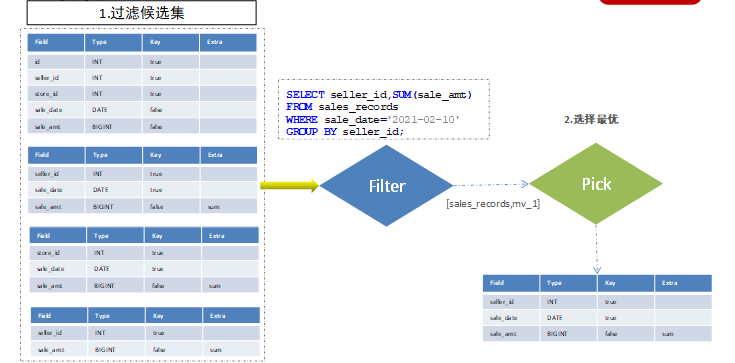
第二部分、线性表详解:数据结构线性表10分钟入门

线性表,数据结构中最简单的一种存储结构,专门用于存储逻辑关系为"一对一"的数据。
线性表,基于数据在实际物理空间中的存储状态,又可细分为顺序表(顺序存储结构)和链表(链式存储结构)。
本章还会讲解顺序表和链表的结合体——静态链表,不仅如此,还会涉及循环链表、双向链表、双向循环链表等链式存储结构。
七、4种算法,实现单链表的反转!
通过前面章节的学习,读者已经对单链表以及它的用法有了一个完整的了解。在此基础上,本节再带领大家研究一个和单链表有关的问题,即如何实现单链表的反转。
反转链表,又可以称为翻转或逆置链表,它们表达的是同一个意思。以图 1 所示的链表为例:

图 1 未反转的链表
经过反转(翻转、逆置)后,得到的新链表如图 2 所示:

图 2 反转后的链表
通过对比图 1 和 图 2 中的链表不难得知,所谓反转链表,就是将链表整体“反过来”,将头变成尾、尾变成头。那么,如何实现链表的反转呢?
常用的实现方案有 4 种,这里分别将它们称为迭代反转法、递归反转法、就地逆置法和头插法。值得一提的是,递归反转法更适用于反转不带头节点的链表;其它 3 种方法既能反转不带头节点的链表,也能反转带头节点的链表。
本节将以图 1 所示,即不带头节点的链表为例,给大家详细讲解各算法的实现思想。
1、迭代反转链表—>更适用于反转不带头节点的链表
该算法的实现思想非常直接,就是从当前链表的首元节点开始,一直遍历至链表的最后一个节点,这期间会逐个改变所遍历到的节点的指针域,另其指向前一个节点。
具体的实现方法也很简单,借助 3 个指针即可。以图 1 中建立的链表为例,首先我们定义 3 个指针并分别命名为 beg、mid、end。它们的初始指向如图 3 所示:
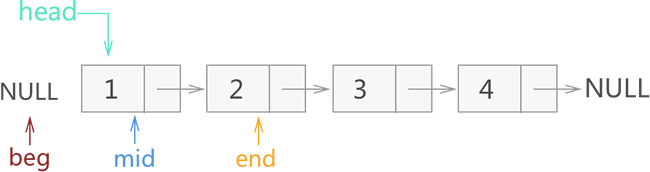
图 3 迭代反转链表的初始状态
在上图的基础上,遍历链表的过程就等价为:3 个指针每次各向后移动一个节点,直至 mid 指向链表中最后一个节点(此时 end 为 NULL )。需要注意的是,这 3 个指针每移动之前,都需要做一步操作,即改变 mid 所指节点的指针域,另其指向和 beg 相同。
1) 在图 3 的基础上,我们先改变 mid 所指节点的指针域指向,另其和 beg 相同(即改为 NULL),然后再将 3 个指针整体各向后移动一个节点。整个过程如图 4 所示:
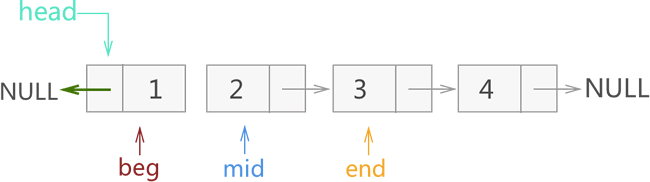
图 4 迭代反转链表过程一
2) 在图 4 基础上,先改变 mid 所指节点的指针域指向,另其和 beg 相同(指向节点 1 ),再将 3 个指针整体各向后移动一个节点。整个过程如图 5 所示:
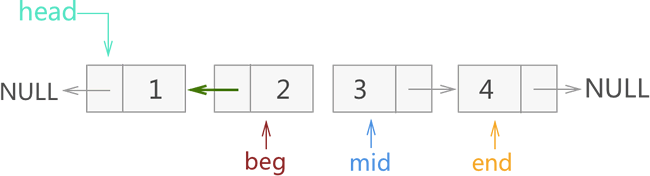
图 5 迭代反转链表过程二
3) 在图 5 基础上,先改变 mid 所指节点的指针域指向,另其和 beg 相同(指向节点 2 ),再将 3 个指针整体各向后移动一个节点。整个过程如图 6 所示:
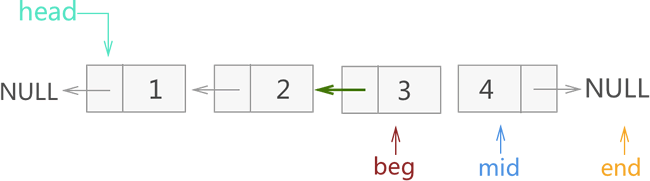
图 6 迭代反转链表过程三
4) 图 6 中,虽然 mid 指向了原链表最后一个节点,但显然整个反转的操作还差一步,即需要最后修改一次 mid 所指节点的指针域指向,另其和 beg 相同(指向节点 3)。如图 7 所示:
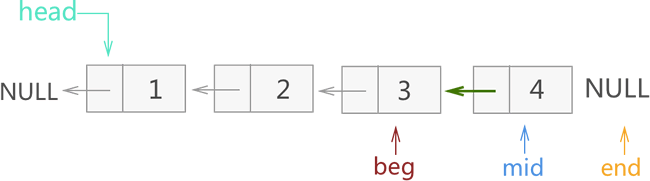
图 7 迭代反转链表过程四
注意,这里只需改变 mid 所指节点的指向即可,不用修改 3 个指针的指向。
5) 最后只需改变 head 头指针的指向,另其和 mid 同向,就实现了链表的反转。
如下是实现整个过程的代码:
//迭代反转法,head 为无头节点链表的头指针
link * iteration_reverse(link* head) {
if (head == NULL || head->next == NULL) {
return head;
}
else {
link * beg = NULL;
link * mid = head;
link * end = head->next;
//一直遍历
while (1)
{
//修改 mid 所指节点的指向
mid->next = beg;
//此时判断 end 是否为 NULL,如果成立则退出循环
if (end == NULL) {
break;
}
//整体向后移动 3 个指针
beg = mid;
mid = end;
end = end->next;
}
//最后修改 head 头指针的指向
head = mid;
return head;
}
}
2、递归反转链表—>既能反转不带头节点的链表,也能反转带头节点的链表。
和迭代反转法的思想恰好相反,递归反转法的实现思想是从链表的尾节点开始,依次向前遍历,遍历过程依次改变各节点的指向,即另其指向前一个节点。
鉴于该方法的实现用到了递归算法,不易理解,因此和讲解其他实现方法不同,这里先给读者具体的实现代码,然后再给大家分析具体的实现过程:
link* recursive_reverse(link* head) {
//递归的出口
if (head == NULL || head->next == NULL) // 空链或只有一个结点,直接返回头指针
{
return head;
}
else
{
//一直递归,找到链表中最后一个节点
link *new_head = recursive_reverse(head->next);
//当逐层退出时,new_head 的指向都不变,一直指向原链表中最后一个节点;
//递归每退出一层,函数中 head 指针的指向都会发生改变,都指向上一个节点。
//每退出一层,都需要改变 head->next 节点指针域的指向,同时令 head 所指节点 的指针域为 NULL。
head->next->next = head;
head->next = NULL;
//每一层递归结束,都要将新的头指针返回给上一层。由此,即可保证整个递归过程中,能够一直找得到新链表的表头。
return new_head;
}
}
仍以图 1 中的链表为例,则整个递归实现反转的过程如下:
1) 由于 head 不为 NULL,因此函数每执行到第 11 行时,递归都会深入一层,并依次将指向节点 2、3、4 的指针作为实参(head_next 的指向)参与递归。而根据递归出口的判断条件,当函数参数 head 指向的是节点 4 时满足 head->next == NULL,递归过程不再深入,并返回指向节点 4 的指针,这就是反转链表的新头指针。
因此,当递归首次退出一层时,new_head 指向的是节点 4 ,而 head 由于退出一层,指向的是节点 3,如图 8 所示。
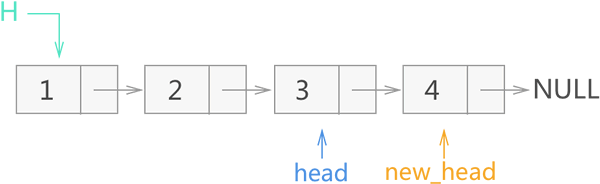
图 8 递归反转链表过程一
2) 在此基础上,开始执行 17、18 行代码,整个操作过程如图 9 所示,最后将 new_head 的指向继续作为函数的返回值,传给上一层的 new_head。
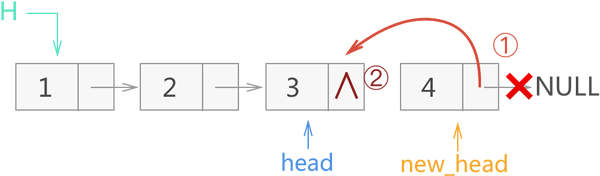
图 9 递归反转链表过程二
注意,图中节点 3 的 next 指针域
∧表示为 NULL。
3) 再退一层,此时 new_head 仍指向节点 4,而 head 退出一层后,指向的是节点 2。在此基础上执行 17、18 行代码,并最终将 new_head 的指向作为函数返回值,继续传给上一层的 new_head。整个操作过程如图 10 所示:
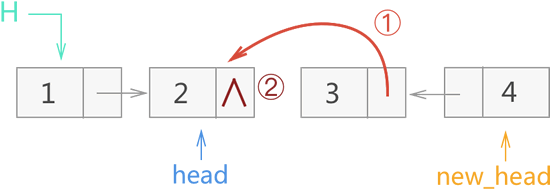
图 10 递归反转链表过程三
4) 再退一层,此时 new_head 仍指向节点 4,而 head 退出一层后,指向的是节点 1。在此基础上执行 17、18 行代码,并返回 new_head。整个操作过程如图 11 所示:
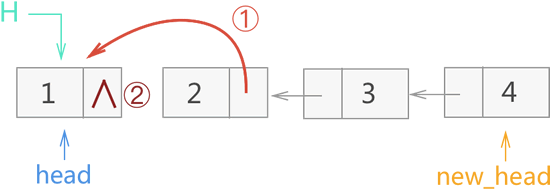
图 11 递归反转链表过程四
head 由节点 1 进入递归,此时 head 的指向又返回到节点 1,整个递归过程结束。显然,以上过程已经实现了链表的反转,新反转链表的头指针为 new_head。
3、头插法反转链表——>既能反转不带头节点的链表,也能反转带头节点的链表。
所谓头插法,是指在原有链表的基础上,依次将位于链表头部的节点摘下,然后采用从头部插入的方式生成一个新链表,则此链表即为原链表的反转版。
仍以图 1 所示的链表为例,接下来为大家演示头插反转法的具体实现过程:
1) 创建一个新的空链表,如图 12 所示:

图 12 创建一个空链表
2) 从原链表中摘除头部节点 1,并以头部插入的方式将该节点添加到新链表中,如图 13 所示:

图 13 从原链表摘除节点 1,再添加到新链表中
3) 从原链表中摘除头部节点 2,以头部插入的方式将该节点添加到新链表中,如图 14 所示:

图 14 从原链表摘除节点 2,再添加到新链表中
4) 继续重复以上工作,先后将节点 3、4 从原链表中摘除,并以头部插入的方式添加到新链表中,如图 15 所示:
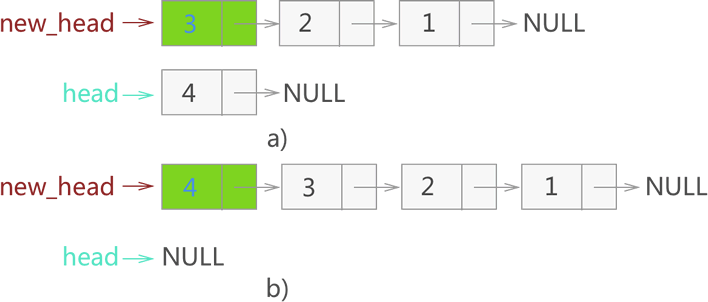
图 15 从原链表摘除节点 3、4,再添加到新链表中
由此,就实现了对原链表的反转,新反转链表的头指针为 new_head。
如下为以头插法实现链表反转的代码:
link * head_reverse(link * head) {
link * new_head = NULL;
link * temp = NULL;
if (head == NULL || head->next == NULL) {
return head;
}
while (head != NULL)
{
temp = head;
//将 temp 从 head 中摘除
head = head->next;
//将 temp 插入到 new_head 的头部
temp->next = new_head;
new_head = temp;
}
return new_head;
}
4、就地逆置法反转链表—>既能反转不带头节点的链表,也能反转带头节点的链表。
就地逆置法和头插法的实现思想类似,唯一的区别在于,头插法是通过建立一个新链表实现的,而就地逆置法则是直接对原链表做修改,从而实现将原链表反转。
值得一提的是,在原链表的基础上做修改,需要额外借助 2 个指针(假设分别为 beg 和 end)。仍以图 1 所示的链表为例,接下来用就地逆置法实现对该链表的反转:
1) 初始状态下,令 beg 指向第一个节点,end 指向 beg->next,如图 16 所示:

图 16 就地反转链表的初始状态
2) 将 end 所指节点 2 从链表上摘除,然后再添加至当前链表的头部。如图 17 所示:
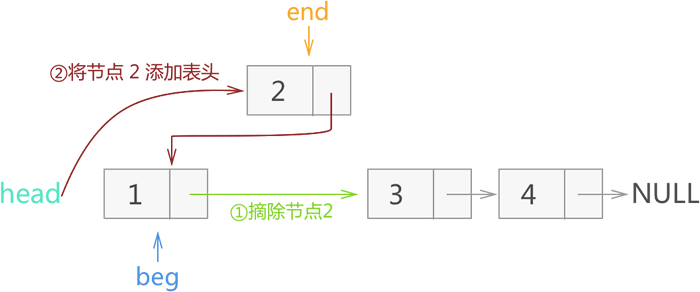
图 17 反转节点 2
3) 将 end 指向 beg->next,然后将 end 所指节点 3 从链表摘除,再添加到当前链表的头部,如图 18 所示:
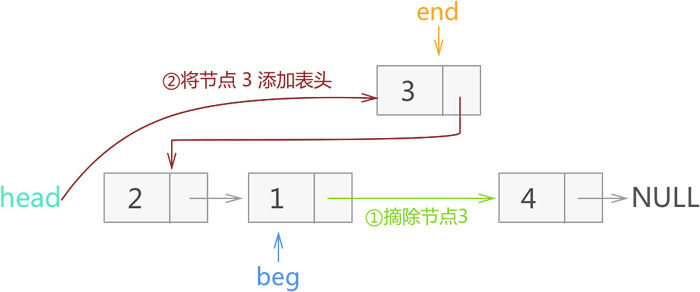
图 18 反转节点 3
4) 将 end 指向 beg->next,再将 end 所示节点 4 从链表摘除,并添加到当前链表的头部,如图 19 所示:
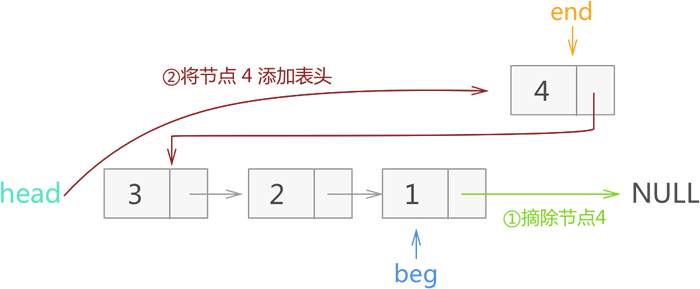
图 19 反转节点 4
由此,就实现了对图 1 链表的反转。
具体实现代码如下:
link * local_reverse(link * head) {
link * beg = NULL;
link * end = NULL;
if (head == NULL || head->next == NULL) {
return head;
}
beg = head;
end = head->next;
while (end != NULL) {
//将 end 从链表中摘除
beg->next = end->next;
//将 end 移动至链表头
end->next = head;
head = end;
//调整 end 的指向,另其指向 beg 后的一个节点,为反转下一个节点做准备
end = beg->next;
}
return head;
}
5、总结
本节仅以无头节点的链表为例,讲解了实现链表反转的 4 种方法。实际上,对于有头节点的链表反转:
- 使用迭代反转法实现时,初始状态忽略头节点(直接将 mid 指向首元节点),仅需在最后一步将头节点的 next 改为和 mid 同向即可;
- 使用头插法或者就地逆置法实现时,仅需将要插入的节点插入到头节点和首元节点之间即可;
- 递归法并不适用反转有头结点的链表(但并非不能实现),该方法更适用于反转无头结点的链表。
结合以上说明,读者可尝试修改本节代码,使它们能用于反转带头节点的链表。对于反转没有头节点的链表,读者可以从反转无节点链表处下载;反之,对于采用迭代法、头插法以及就地逆置法反转有头节点的链表,读者可从反转有节点链表处下载。
八、如何判断两个单链表相交?
判断 2 个单链表是否相交,是一个老生常谈但又极具思考性的面试题,本节就在读者已经掌握单链表及其基本操作的基础上,就此问题给大家做深入地讲解。
首先,读者要搞清楚“相交”的含义。所谓相交,是指有公共的部分,而 2 个单链表相交,则意味着它们有公共的节点,公共节点的数量可以是 1 个或者多个。
通过前面的学习我们知道,单链表是线性表的一种,如果我们将 2 个单链表看做 2 条线段的话,图 1 模拟了 2 条线段相交的所有可能情况。
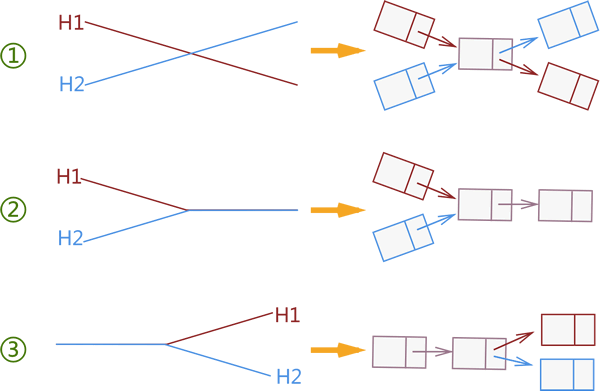
图 1 链表相交
注意,结合“单链表中每个节点有且仅有 1 个指针域”的特性,如 1 所示的这 3 种情况中,只有第 2 种情况符合单链表的特性,另外 2 种情况则破坏了此特性。经过以上的分析,本节要验证 2 个单链表是否相交,实际上等同于判断 2 个单链表是否和图 1② 所示的存储结构相同。
判断 2 个单链表(下文分别称它们为链表 1 和链表 2 )是否相交,常用的方法有如下几种。
1) 分别遍历链表 1 和链表 2,对于链表 1 中的每个节点,依次和链表 2 中的各节点进行比对,查看它们的存储地址是否相同,如果相同,则表明它们相交;反之,如果链表 1 中各节点的存储地址,和链表 2 中的各个节点都不相同,则表明它们不相交。
注意,此方法中比较的是节点的存储地址,而非数据域中存储的元素。原因很简单,数据域中存储元素值相同,并不是 2 个单链表相交的充分条件,因为 2 个不相交的链表中很可能存有相同的元素。
仍以前面章节中构建的单链表为例:
typedef struct Link {
char elem; //代表数据域
struct Link * next; //代表指针域,指向直接后继元素
}link; //link为节点名,每个节点都是一个 link 结构体
在此基础上,判断 2 个单链表是否相交的实现代码为:
//自定义的 bool 类型
typedef enum bool
{
False = 0,
True = 1
}bool;
//L1 和 L2 为 2 个单链表,函数返回 True 表示链表相交,返回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) {
link * p1 = L1;
link * p2 = L2;
//逐个遍历 L1 链表中的各个节点
while (p1)
{
//遍历 L2 链表,针对每个 p1,依次和 p2 所指节点做比较
while (p2) {
//p1、p2 中记录的就是各个节点的存储地址,直接比较即可
if (p1 == p2) {
return True;
}
p2 = p2->next;
}
p1 = p1->next;
}
return False;
}
通过分析 LinkIntersect() 函数的实现过程不难得知,无论 2 个链表是否相交,此实现方式的时间复杂度为O(。)
有关时间复杂度的计算过程,读者可阅读《第一部分:四、时间复杂度和空间复杂度(详解版)》一节,这里不再做过多赘述。
2) 实际上,第 1 种实现方案还可以进一步优化。结合图 1②,2 个单链表相交有一个必然结果,即这 2 个链表的最后一个节点必定相同;反之,如果 2 个链表不相交,则这 2 个链表的最后一个节点必定不相同。
由此,可以对以上实现代码进行优化:
//L1 和 L2 为 2 个单链表,函数返回 True 表示链表相交,返回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) {
link * p1 = L1;
link * p2 = L2;
//找到 L1 链表中的最后一个节点
while (p1->next) {
p1 = p1->next;
}
//找到 L2 链表中的最后一个节点
while (p2->next)
{
p2 = p2->next;
}
//判断 L1 和 L2 链表最后一个节点是否相同
if (p1 == p2) {
return True;
}
return False;
}
显然经过优化,该函数的时间复杂度就缩小为O(n)。
3) 针对第 1 种实现方案的优化,除了第 2 种方式,还有一种思想。
假设 L1 和 L 2 相交,则两个链表中相交部分节点的数量一定是相等的。如图 2 所示:

图 2 两个链表相交
可以看到,L1 和 L2 相交,绿色部分节点为 L1 和 L2 链表的相交部分。
也就是说,如果 2 个链表相交,那么它们相交部分所包含的节点个数一定相等。在此基础上,我们可以这样优化第 1 种实现方案,以图 2 中的 L1 和 L2 为例,从 L1 尾部选取和 L2 链表等长度的一个子链表(也也就是图 3 中的 temp 子链表),同时遍历 temp 和 L2 链表,依次判断 2 个遍历节点是否相同,如果相同则表明 L1 和 L2 相交;反之则不相交。
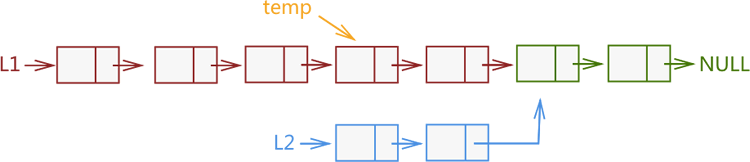
图 3 在较长链表中找到和较短链表等长度的子链表
此实现方案的实现代码如下:
//L1 和 L2 为 2 个单链表,函数返回 True 表示链表相交,返回 False 表示不相交
bool LinkIntersect(link * L1, link * L2) { l
ink * plong = L1;
link * pshort = L2;
link * temp = NULL;
int num1 = 0, num2 = 0, step = 0;
//得到 L1 的长度
while (plong) {
num1++;
plong = plong->next;
}
//得到 L2 的长度
while (pshort)
{
num2++;
pshort = pshort->next;
}
//重置plong和pshort,使plong代表较长的链表,pshort代表较短的链表
plong = L1;
pshort = L2;
step = num1 - num2;
if (num1 < num2) {
plong = L2;
pshort = L1;
step = num2 - num1;
}
//在plong链表中找到和pshort等长度的子链表
temp = plong;
while (step) {
temp = temp->next;
step--;
}
//逐个比较temp和pshort链表中的节点是否相同
while (temp && pshort) {
if (temp == pshort) {
return True;
}
temp = temp->next;
pshort = pshort->next;
}
return False;
}
相比第 2 种方案,此方法的实现逻辑虽然复杂,但优点是,该方法可以找到 2 个单链表相交的交点(也就是相交时的第一个节点),也就是使 LinkIntersect() 函数返回 True 时的 temp 指针指向的那个节点。另外,此方案的时间复杂度也为O(n)。
1、总结
总的来说,本节讲解了 3 种“判断 2 个链表是否相交”的方法,其中第 2、3 种方案的时间复杂度都比第 1 种要小。
从另一个角度比较这 3 种方案,第 1 种和 第 3 种在判断“2 个链表是否相交”的同时,还能找到它们相交的交点,而第 2 种实现方案则不具备这个功能。
如果读者想实现“判断 2 个链表是否相交,如果相加找到交点”这样的功能,只需对第 1、3 种方案的实现代码做略微调整即可。由于很简单,读者可自行尝试实现。