1.题目

2.解答

2.1模型假设

1.体重增加正比于吸收的热量，平均每8000kcal增加体重1kg

2.身体正常代谢引起的体重减少正比于体重，每周每千克体重消耗热量一般在200kcal至320kcal之间，且因人而异，这相当于体重70kg的人每天消耗2000kcal至3200kcal

3.运动引起的体重减少正比于体重，且与运动形式和运动时间有关

4.为了安全与健康，每周吸收热量最好不要小于10000kcal，且每周减少量不要超过1000kcal，每周体重减少不要超过1.5kg

2.2基本模型：

记第k周（初）体重为w(k)(kg)，第k周吸收热量为c(k)(kcal)，k=1，2…。设热量转换系数为α。深体代谢消耗系数为β，根据模型假设，正常情况下（不考虑运动）体重变化的基本方程为(只要能表示这段方程，主体部分基本就完事，使用一个while循环或者for循环即可）
$$w(k+1)=w(k)+\alpha c(k)-\beta w(k),k=1,\mathrm{2...}$$
根据假设1，当确定一个人的代谢消耗系数β后，就可按照上述式子由每周吸收的热量c(k)推到ta体重w(k)的变化，增加运动时，需要更改消耗系数β值，具体会在下面给出

2.3第一问：

第一阶段：
条件：
$$W(k+1)-w(k)=1.1$$
$$c=(w-1.1+(b-1)\ast w)/a$$
$$b=a\ast c/w;$$
初始参数：
c=25000;
h=1.66;身高
w=114;体重
a=1/8000;

代码：

clc;clear;
c=25000;
h=1.66;

w=114;
a=1/8000;
b=a*c/w;
k=0;
while c>=10000
    disp("第"+(k+1)+"周")
    c=(w-1.1+(b-1)*w)/a
    w=w-1.1
    k=k+1;
end

结果：

共需27周
第二阶段：

k1=0
while bmi>=25
    w=(1-b)*w+a*c
    bmi=w/(h*h)
    k1=k1+1;
end

共需19周
总共46周

2.4第二问：

若想加快进程，需要增加运动，根据前面运动消耗表，记热量消耗为γ，每周运动t小时，则基本模型中β改为β+αγt，此时方程为
$$w(k+1)=w(k)+\alpha c(k)-(\beta +\alpha \gamma t)w(k)$$
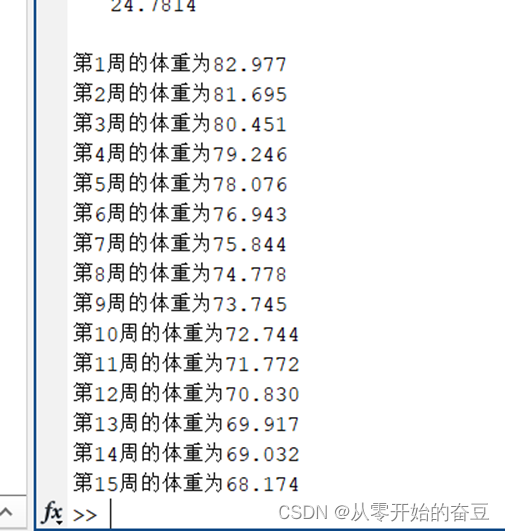
我们选择乒乓，共15周

beta=b;
weight= 84.3;
sport=1;
category="pq";
time=0;
if sport
    sport_cate = containers.Map({'run', 'dance', 'pq', 'bicycle', 'swim'}, [7.0, 3.0, 4.4, 2.5, 7.9]);
    keys = sport_cate.keys;
    for i = 1:length(keys)
        if strcmp(category, keys{i})
            s = sport_cate(category);
            while weight/(h*h) > 25
                weight = weight + a * c - weight * (beta + a * s * 8);
                time = time + 1;
                fprintf('第%d周的体重为%.3f\n', time, weight);
            end
        end
    end
else
    while weight/(h*h) > 25
        a = 1 / 8000;
        weight = weight * (1-beta) + a * c;
        time = time + 1;
        fprintf('第%d周的体重为%.3f\n', time, weight);
    end
    
end

2.5第三问：

吸收热量不变，若运动，吸收热量增加