66ccff
单纯形法是解线性规划问题(LP)的最经典方法,很多人都了解单纯形法是用单纯形表来进行求解的,但是不了解背后的原理。
这篇博文介绍单纯型表的直觉。
需要的前置知识
- 你需要了解:
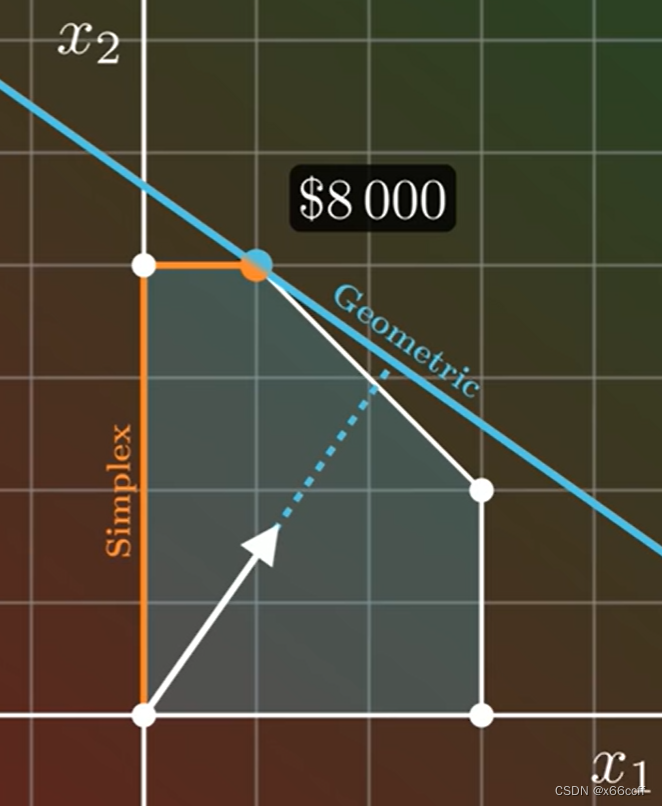
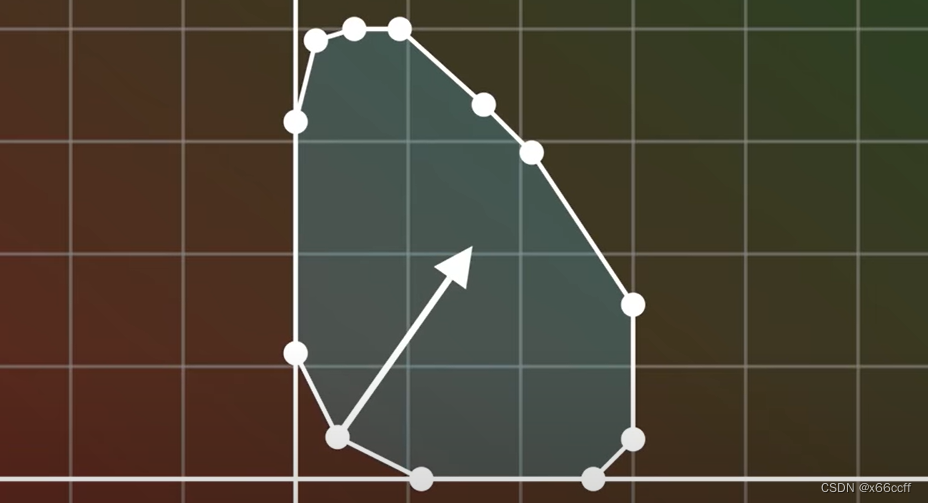
- 单纯形法实际上是在“爬山”,从任意一个边界点开始,每次沿着边界走,直到目标值无法继续上升。
- 线性规划由于线性性质,问题对应的单纯形上的边界关于函数值的变化都是单调的。
- 可以引入松弛变量将不等式约束转化为等式,以及所有变量 > = 0 >=0 >=0的约束
形式
对于这样的一个线性规划问题:
x
1
,
x
2
≥
0
x_{1},x_{2}\geq0
x1,x2≥0
x
1
≤
3000
x_1 \le 3000
x1≤3000
x
2
≤
4000
x_2 \le 4000
x2≤4000
x
1
+
x
2
≤
5000
x_1+x_2 \le 5000
x1+x2≤5000
max
1.2
x
1
+
1.7
x
2
\max 1.2x_1+1.7 x_2
max1.2x1+1.7x2
可以对每一个不等式引入松弛变量:
紧 : x 1 , x 2 ,松: s 1 , s 2 , s 3 紧:x_1,x_2,松:s_1,s_2,s_3 紧:x1,x2,松:s1,s2,s3
x
1
,
x
2
,
s
1
,
s
2
,
s
3
≥
0
x_{1},x_{2},s_1,s_2,s_3\geq0
x1,x2,s1,s2,s3≥0
x
1
+
s
1
=
3000
x_1+\red{s_1}= 3000
x1+s1=3000
x
2
+
s
2
=
4000
x_2+\red{s_2}= 4000
x2+s2=4000
x
1
+
x
2
+
s
3
=
5000
x_1+x_2 +\red{s_3}= 5000
x1+x2+s3=5000
max
1.2
x
1
+
1.7
x
2
\max 1.2x_1+1.7 x_2
max1.2x1+1.7x2
一些直觉
- 当前的问题的维度 n n n,实际上就是基变量的个数(在这里 n = 2 n=2 n=2)
- 基变量,就是紧的,在当前点满足其 ≥ 0 \ge0 ≥0约束的变量;松弛变量则在当前点不满足 ≥ 0 \ge0 ≥0约束。
- 在边界上移动时,有且只能有 n n n个 ≥ 0 \ge0 ≥0约束被满足(在这里 n = 2 n=2 n=2)
- 单纯形法的步骤:
- step1: 选择出基变量(从该变量对应的
>
=
0
>=0
>=0约束边界上面离开) 选择标准有很多,经典的标准是:能使得目标函数上升最快,斜率
k
k
k系数最大的一个
- 在这个例子里,如果我们从 ( 0 , 0 ) (0,0) (0,0)开始,则应该选择 x 2 x_2 x2 ,因为它具有系数 1.7 1.7 1.7
- step2: 选择入基变量(走到该变量对应的 > = 0 >=0 >=0约束边界上),直观理解,就是问:随着我的出基变量逐渐增大,先碰到哪一个约束? 这里 x 1 x_1 x1 是基变量,所以 = 0 =0 =0;也就是问在 x 2 + s 1 = 4000 x_2+s_1=4000 x2+s1=4000和 0 + x 2 + s 3 = 5000 0+x_2+s_3=5000 0+x2+s3=5000 这两个约束中,随着 x 1 x_1 x1增大,哪一个先使得非基变量=0?显然是 s 1 s_1 s1, 因为 5000 1 > 4000 1 \frac{5000}{1}>\frac{4000}{1} 15000>14000。也就是说,我们比较每一个约束里面常数和非基变量的系数之比,选择最小的(注意:对于 s i = 3000 + x j s_i=3000\red{+}x_j si=3000+xj这样形式的约束我们不考虑,因为 x j x_j xj增大永远无法使得 s j = 0 s_j=0 sj=0(对应单纯形表要求比值非正数)),即可找到最先满足约束的那个变量,即我们的入基变量 s 1 s_1 s1
- 直到用基变量表示的目标函数里面每一个变量系数都小于0,就说明无法再通过增大变量值使得目标值增大,于是算法找到最优解,停止。
- step1: 选择出基变量(从该变量对应的
>
=
0
>=0
>=0约束边界上面离开) 选择标准有很多,经典的标准是:能使得目标函数上升最快,斜率
k
k
k系数最大的一个
从(0,0)开始
紧 : x 1 , x 2 ,松: s 1 , s 2 , s 3 紧:x_1,x_2,松:s_1,s_2,s_3 紧:x1,x2,松:s1,s2,s3
x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 x_{1},x_{2},s_1,s_2,s_3\geq0 x1,x2,s1,s2,s3≥0
R
H
S
都用基变量表示
RHS都用基变量表示
RHS都用基变量表示
s
1
=
3000
−
x
1
s_1=3000-x_1
s1=3000−x1
s
2
=
4000
−
x
2
s_2=4000-x_2
s2=4000−x2
s
3
=
5000
−
x
1
−
x
2
s_3=5000-x_1-x_2
s3=5000−x1−x2
max
1.2
x
1
+
1.7
x
2
\max 1.2x_1+1.7 x_2
max1.2x1+1.7x2
进行一次迭代之后:( x 2 x_2 x2松, s 2 s_2 s2紧)
紧 : x 1 , s 2 ,松: x 2 , s 1 , s 3 紧:x_1,\red{s_2},松:\blue{x_2},s_1,s_3 紧:x1,s2,松:x2,s1,s3
x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 x_{1},x_{2},s_1,s_2,s_3\geq0 x1,x2,s1,s2,s3≥0
R
H
S
都用基变量表示
RHS都用基变量表示
RHS都用基变量表示
s
1
=
3000
−
x
1
s_1=3000-x_1
s1=3000−x1
x
2
=
4000
−
s
2
\blue{x_2} = 4000-\red{s_2}
x2=4000−s2
s
3
=
1000
−
x
1
+
s
2
s_3=\green{1000 -x_1 + s_2}
s3=1000−x1+s2
max
1.2
x
1
+
1.7
(
4000
−
s
2
)
=
1.2
x
1
+
6800
−
1.7
s
2
\max 1.2x_1+1.7 \green{(4000-s_2)} = 1.2x_1 + 6800 - 1.7s_2
max1.2x1+1.7(4000−s2)=1.2x1+6800−1.7s2
再进行一次迭代:( x 1 x_1 x1松, s 3 s_3 s3紧)
紧 : s 3 , s 2 ,松: x 2 , x 1 , s 1 紧:\red{s_3},\red{s_2},松:\blue{x_2},\blue{x_1},s_1 紧:s3,s2,松:x2,x1,s1
x 1 , x 2 , s 1 , s 2 , s 3 ≥ 0 x_{1},x_{2},s_1,s_2,s_3\geq0 x1,x2,s1,s2,s3≥0
R
H
S
都用基变量表示
RHS都用基变量表示
RHS都用基变量表示
x
1
=
3000
−
s
1
x_1 = 3000 -s_1
x1=3000−s1
x
2
=
4000
−
s
2
\blue{x_2} = 4000-\red{s_2}
x2=4000−s2
x
1
=
1000
−
s
3
+
s
2
\blue{x_1} = 1000 -s_3+s_2
x1=1000−s3+s2
max
1.2
x
1
+
6800
−
1.7
s
2
=
1.2
(
1000
−
s
3
+
s
2
)
+
6800
−
1.7
s
2
=
8000
−
1.2
s
3
−
0.5
s
2
\max 1.2x_1 + 6800 - 1.7s_2 = 1.2\green{(1000 -s_3+s_2)} + 6800 - 1.7s_2 =\purple{ 8000 -1.2s_3-0.5s_2}
max1.2x1+6800−1.7s2=1.2(1000−s3+s2)+6800−1.7s2=8000−1.2s3−0.5s2
注意到:因为变量前面的系数都小于0,因此无法继续改进,我们此时达到了最优值 8000