数据统计的一些专业术语学习
- 1. 极差
- 2. 方差
- 3. 标准差
- 4. 均值绝对差
1. 极差
数据统计的极差,又称全距,是指一组数据中最大值和最小值之差。
举个例子,如果我们有一组数据:1,2,3,4,5,那么这组数据的极差就是:
5 - 1 = 4
也就是说,这组数据中最大的数是5,最小的数是1,两者之差是4。
对于小学生来说,可以用以下例子来理解极差:
假设小明班上的同学身高分别是120厘米、130厘米、140厘米、150厘米、160厘米。那么,这组数据的极差就是:
160 - 120 = 40
也就是说,小明班上同学最高的是一个160厘米的男孩,最矮的是一个120厘米的女孩,两者之差是40厘米。
从这个例子可以看出,极差可以用来衡量一组数据的离散程度。如果极差较大,说明数据分布较为分散;如果极差较小,说明数据分布较为集中。
在实际生活中,极差也有很多应用场合,例如:
- 衡量考试成绩的离散程度
- 衡量产品质量的离散程度
- 衡量经济指标的离散程度
等等。
2. 方差
数据统计的方差,是用来衡量一组数据离散程度的度量。它反映了数据分布中各个数据点与平均数之间的差距有多大。
举个例子,假设我们有一组数据:1,2,3,4,5。那么,这组数据的平均数是3。
如果这五个数据都离平均数很近,比如都是2、3、4、4、5,那么这组数据的方差就比较小。
如果这五个数据离平均数很远,比如是1、5、9、13、17,那么这组数据的方差就比较大。
对于小学生来说,可以用以下例子来理解方差:
假设小明班上有10个同学,他们的身高分别是1米60、1米70、1米80、1米90、1米100。那么,这10个同学的平均身高是1米75。
如果这10个同学的身高都比较接近平均身高,比如都是1米70左右,那么这组数据的方差就比较小。
如果这10个同学的身高差距比较大,比如有个同学只有1米60,有个同学却有1米90,那么这组数据的方差就比较大。
从这个例子可以看出,方差可以用来衡量一组数据的离散程度。如果方差比较小,说明数据分布比较集中,数据比较接近平均数。如果方差比较大,说明数据分布比较分散,数据离平均数比较远。
在实际生活中,方差也有很多应用场合,例如:
- 用于衡量经济指标的稳定性
- 用于衡量产品质量的一致性
- 用于衡量实验结果的可靠性
等等。
3. 标准差
数据统计的标准差是指一组数据的分散程度。它是用来衡量数据的离散程度。标准差越大,数据越分散;标准差越小,数据越集中。
举个例子,如果我们有一组数据:1,2,3,4,5,那么这组数据的标准差是1.41。
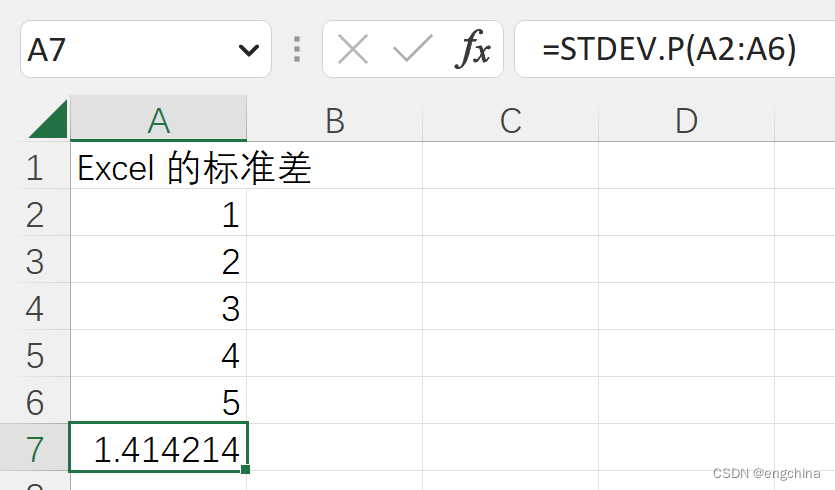
这意味着,这组数据的平均值是3,但数据分散在平均值的周围。有些数据比平均值高,有些数据比平均值低。
如果我们有一组数据:2,2,2,2,2,那么这组数据的标准差是0。
这意味着,这组数据的所有数据都是相同的,因此没有分散。
对于小学生来说,可以用以下例子来理解标准差:
假设小明身高是150厘米,小红身高是155厘米,小华身高是160厘米。那么,这三人的身高平均值是155厘米。
标准差可以用来衡量这三人身高的分散程度。如果标准差较大,那么这三人身高的差异就较大。如果标准差较小,那么这三人身高的差异就较小。
在这种情况下,小明身高比平均值低5厘米,小华身高比平均值高5厘米。因此,这两人的身高与平均值的差距较大,标准差也较大。
而小红身高与平均值的差距较小,因此标准差也较小。
从这个例子可以看出,标准差可以用来衡量数据的离散程度。
在实际生活中,标准差也有很多应用场合,例如:
- 衡量考试成绩的差异
- 衡量产品质量的一致性
- 衡量经济指标的波动性
等等。
4. 均值绝对差
数据统计的均值绝对差,也称为平均绝对偏差,是指一组数据与其平均值之差的绝对值的平均数。它是用来衡量数据的离散程度的另一种方法。
举个例子,如果我们有一组数据:1,2,3,4,5,那么这组数据的均值绝对差是1.2。
这意味着,这组数据的平均值是3,但数据分散在平均值的周围。有些数据比平均值高,有些数据比平均值低。
假设我们有5个学生的考试成绩:
小明:90分
小红:80分
小刚:70分
小楠:85分
小青:95分
首先,我们计算出这5个数字的平均数(算术平均数):
(90 + 80 + 70 + 85 + 95) / 5 = 84
然后,计算每个数字与平均数的差值的绝对值:
|90 - 84| = 6
|80 - 84| = 4
|70 - 84| = 14
|85 - 84| = 1
|95 - 84| = 11
最后,把这些绝对差值求平均数,就得到了均值绝对差:
(6 + 4 + 14 + 1 + 11) / 5 = 7.2
所以这个例子中的均值绝对差是7.2。
均值绝对差反映了数据与平均值的偏离程度,它比标准差对异常值不那么敏感,可以更好地反映数据的真实分散程度。
在实际生活中,均值绝对差也有很多应用场合,例如:
- 衡量考试成绩的差异
- 衡量产品质量的一致性
- 衡量经济指标的波动性
等等。
与标准差相比,均值绝对差的优点是它不受极端值的影响。例如,如果我们将一组数据中的最大值和最小值都增加100,那么标准差也会增加,但均值绝对差不会增加。
未完待续!