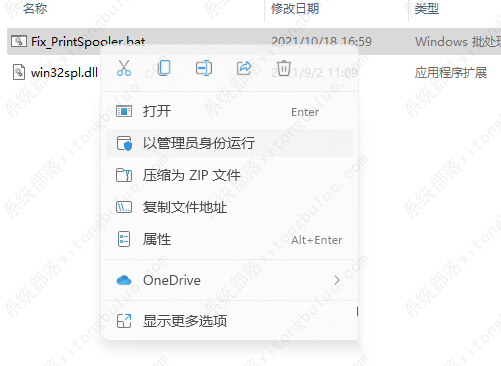
二叉树是一种特殊的树形结构，每个结点最多只有两棵子树，即度最大为2，且二叉树左右子树不能颠倒。

主要常见分类有：

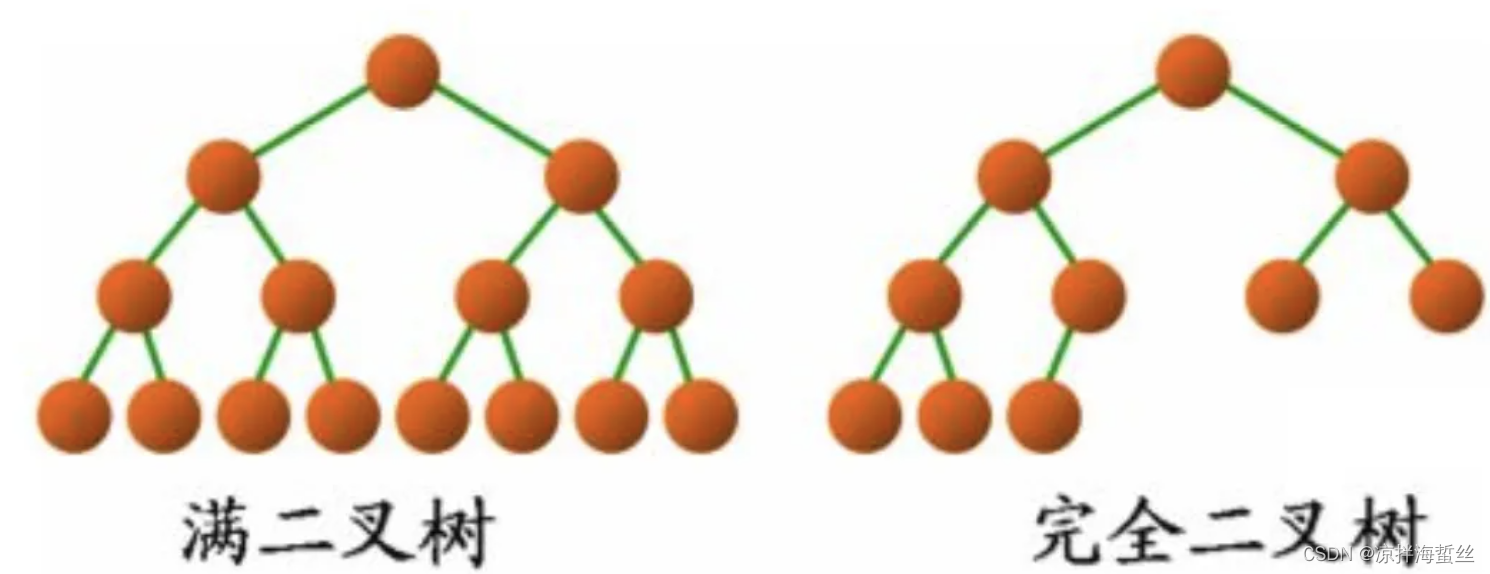
满二叉树：

除了叶子结点外，每个结点的度数都是2，若高度为h，则一定有2^h - 1个结点，树如其名，一定是装得满满的一棵树，同时这个公式也用来判断高度为h的二叉树最多的结点数。

完全二叉树：

它可以不满，但是完全二叉树的结点存放顺序一定要是从左开始依次放，不允许有些结点有右孩子但没有左孩子
叶子结点只有可能出现在最后一层和倒数第二层
若有度为1的结点，有且只能有一个，且该结点只有左孩子没有右孩子
若总结点数n是奇数，则每个分支结点都有左右孩子
若总结点数n是偶数，则最后一个分支结点（编号n/2）只有左孩子没有右孩子

常用公式：

（1）叶子结点数 = 度为2的结点数 + 1 ； n0 = n2 + 1
（2）二叉树第k层最多有 2^(k-1) 个结点
（3）高度为h的二叉树最多有2^h - 1个结点 （即满二叉树）
（4）有n个结点的完全二叉树的高度：log2(n+1) 向上取整 或者 log2n + 1 向下取整

题目通过是给出结点数求最大高度，最小高度，或者给出高度求最少多少结点，最多有多少结点（要看清楚题目给出的二叉树是普通二叉树，还是满二叉树还是完全二叉树是关键）

（1）假设一棵二叉树结点数为50，则它最小高度是：
注意该题目没说是完全二叉树，也就是说它结点是想怎么放就怎么放的。但是又因为要高度最小，只能按照满二叉树的形式去放才能保证高度最小
那么根据满二叉树的公式：log2(50+1) 向上取整，得到6

（2）一棵具有1025个结点的二叉树的高为：11～1025
注意该题目只是普通二叉树，所以它的高最大可以是1025，最小的话按照满二叉树放，log2(1025+1)向上取整 = 11层

（3）二叉树只有度为0和2的结点，结点总数15，则该二叉树的最大深度是：
注意题目是普通二叉树，规定只有度为0和2，那么就可以是一棵单边树，即只往左或者右延伸

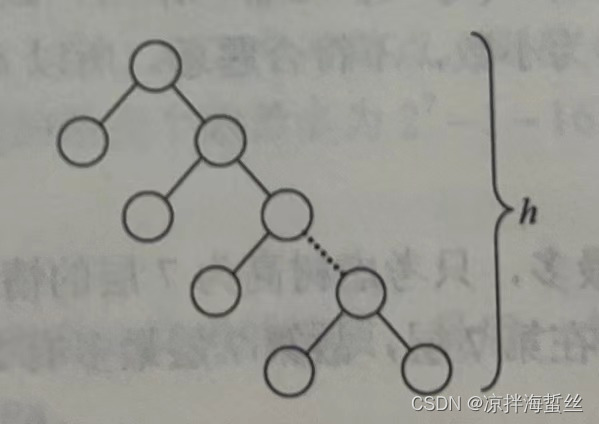
按照这个规律推，第一行1个，第二行开始，每一层都是2个，那么总结点数就是 : 2*h - 1 = 15
解出 h = 8

（4）高度为h的完全二叉树最少有（）个结点
注意是完全二叉树，高度为h，还要求最少的结点数，那么我们可以让h-1层是满的，h层只放一个敷衍了事
那么就是：2 ^(h-1) - 1(第h-1层的个数) + 1(第h层的1个) = 2 ^(h-1) 个

（5）已知一棵完全二叉树第六层有8个叶子结点，则完全二叉树的结点个数最少是：
完全二叉树第六层只有8个，要结点数最少，则前五层是满的：2 ^(5) - 1 = 31
第六层只有8个，则 31 + 8 = 39

（6）若一棵深度为6的完全二叉树的第六层有3个叶子结点，则该二叉树共有 （） 个叶子结点
因为完全二叉树只有六层，第六层不满，前五层满，根据公式，第五层有 2^5-1 = 16个结点，又因为第六层有3个叶子，3个叶子结点会占用第五层2个结点，所以第五层的叶子结点数： 16 - 2 = 14
总叶子结点数：14 + 3 = 17

（7）一棵完全二叉树上有1001个结点，其中叶子结点的个数是：
直接求非叶子结点的最大编号是 ： 1001/2 向下取整 = 500
叶子结点= 总结点 - 非叶子结点 = 1001 - 500 = 501

（8）若一棵二叉树有126个结点，在第七层至多有（63）个结点
思路一：
要第七层结点最多，则第六层必须满，这样第六层的父辈才能往下生长结点，那么照推第五层也必须满…
若前六层满，则 共有 2^6 - 1 = 63 个
那么剩下给第七层的就只有 ： 126 - 63 = 63

思路二：
若是满七层，共需要：2^7 - 1 = 127个结点
可是题目说只有126个，那么少的那一个只可能少在第七层
第七层如果是满的话，应该是： 2^h-1 = 64 个
现在少了一个，所以只有：63个

（9）一棵有124个叶子结点的完全二叉树，最多有（）个结点
总结点数为 n
则 n = n0 + n1 + n2
又因为公式有 n0 = n2 + 1
n2 = n0 - 1
所以 n = n0 + n1 + n0 -1 = 2n0 - 1 + n1
得到总数n = 2*124 -1 + n1
这个时候，度为1的结点数要么有一个要么0个，因为它是完全二叉树啊！不可能有两个度为1的结点。
那么题目要求结点最多能有多少，那么就是1个度为1
n=248
这道题很巧妙，不管度为1的结点存不存在，都不会影响124个叶子结点这个题目要求，为了结点最多，我们就应该设度为1的有一个

（10）一棵有n个结点的二叉树采用二叉链式存储结点，其中空指针数为：
首先想象二叉树的链式存储，是用双向链表的结构存的，左右孩子各占一个指针域嘛，所以n个结点就会有2n个指针，又因为一条边就代表着一个指针指向下一个元素，也就是指针不为空；但是n个结点的二叉树，边数只有 n - 1条啊（根结点头顶上没有边指向它），所以按照分析，一条边能使一个指针域不空，那么空指针就为： 2n - (n-1) = n + 1

或者更简单画图，画个三个结点的二叉树，就会发现空指针域是4（两个叶子结点的左右孩子指针都是空的），7个结点的二叉树，空指针是8（4个叶子结点的左右孩子指针都空）…

（11）【2009】已知一棵完全二叉树的第六层有8个叶子结点，则该完全二叉树的结点个数最多是：
为了结点数最多，我们可以假设有七层，第七层不满，这样第六层就会产生叶子结点
若有第七层，则第七层最多有：2^7-1 = 64 个结点，且第七层的全部是叶子结点，但是第六层要有8个叶子，也就是可以想象成第六层有8个结点没有生育能力，无法生孩子，那么第七层就会少 2*8 = 16个结点
所以第七层只有64 - 16 = 48 个叶子

那么总的结点个数就是前满六层 + 第七层的48 = 2^6 - 1 + 48 =111个

（12）【2011】若一棵完全二叉树有768个结点，则该二叉树中叶子结点的个数是：
768 / 2 向下取整 = 384 个非叶子
叶子结点=总结点 - 非叶子结点 = 384

（13）【2018】设一棵非空完全二叉树T的所有叶子结点均位于同一层，且每个非叶子结点都有2个子结点。若T有K个叶子结点，则T的结点总数是：
题目意思就是，凡是能生孩子的都生了两个，而且所有孩子都在同一层，整个家族团团圆圆和和美美，这是啥？这不就是满二叉树
K个叶子
度为1的n1没有
公式 : k = n0(叶子) = n2 + 1
即 n2 = k - 1
总结点 n = n2 + n0 = k - 1 + k = 2k -1

（14）【2020】对于任意一棵高度为5且有10个结点的二叉树，若采用顺序存储结构保存，每个结点占用1个存储单元，则存放该二叉树需要的存储单元数量至少是：
首先注意它只是普通二叉树，高度为5，且只有10个结点
其次注意它要求：存储单元数量至少
至少的意思是：我这棵树随便摆的情况下，多少个存储单元能装得下
所以我们应该考虑5层满二叉，其实它不是五层满二叉
但是，顺序存储结构的特点就是：空的结点也会占用一个存储空间，所以当该随便摆的普通二叉树的大量结点堆满了右侧，左侧为空，其实左侧还是会占用存储空间，所以只能按五层满二叉计算
所以得：2^5 - 1 = 31 个存储单元