算法逆袭之路（1）

11.29

开始跟进算法题进度!

每天刷4题左右 ,一周之内一定要是统一类型

而且一定稍作总结, 了解他们的内在思路究竟是怎样的!!

12.24

一定要每天早中晚都要复习一下

早中午每段一两道, 而且一定要是同一个类型, 不然刷起来都没有意义

12.26/27：

斐波那契数

爬楼梯

最小花费爬楼梯

不同路径1/2

12.28：

整数拆分

重点思路：一个正整数可以分为两个，或者多个，多个可以用dp[i-j]代替，一定不能直接分为乘以dp的情况，因为这就默认了必须拆分为三个以上

不同的二叉搜索树

重点思路：把左右子树所有情况乘起来，递归子树的问题。注意左右节点个数的边界

12.29

01背包理论

12.30

分割等和子集

很难看出来是01背包。满足的条件有

每个元素只有取和不取两个状态
结果要满足，某一部分和，刚好等于什么什么value，而背包问题是在限制的重量内计算他们价值最大值，这里只需把求最大值改成求刚好 == sum即可
此题的weight和value都是nums【i】，因为是一个一个数字要求刚好和为sum
dp【i】代表在i内之和最大为多少本题要求刚好等于sum所以结束条件是dp[ sum ] == sum ，即总量为sum之内刚好最大为sum！

581. 最短无序连续子数组

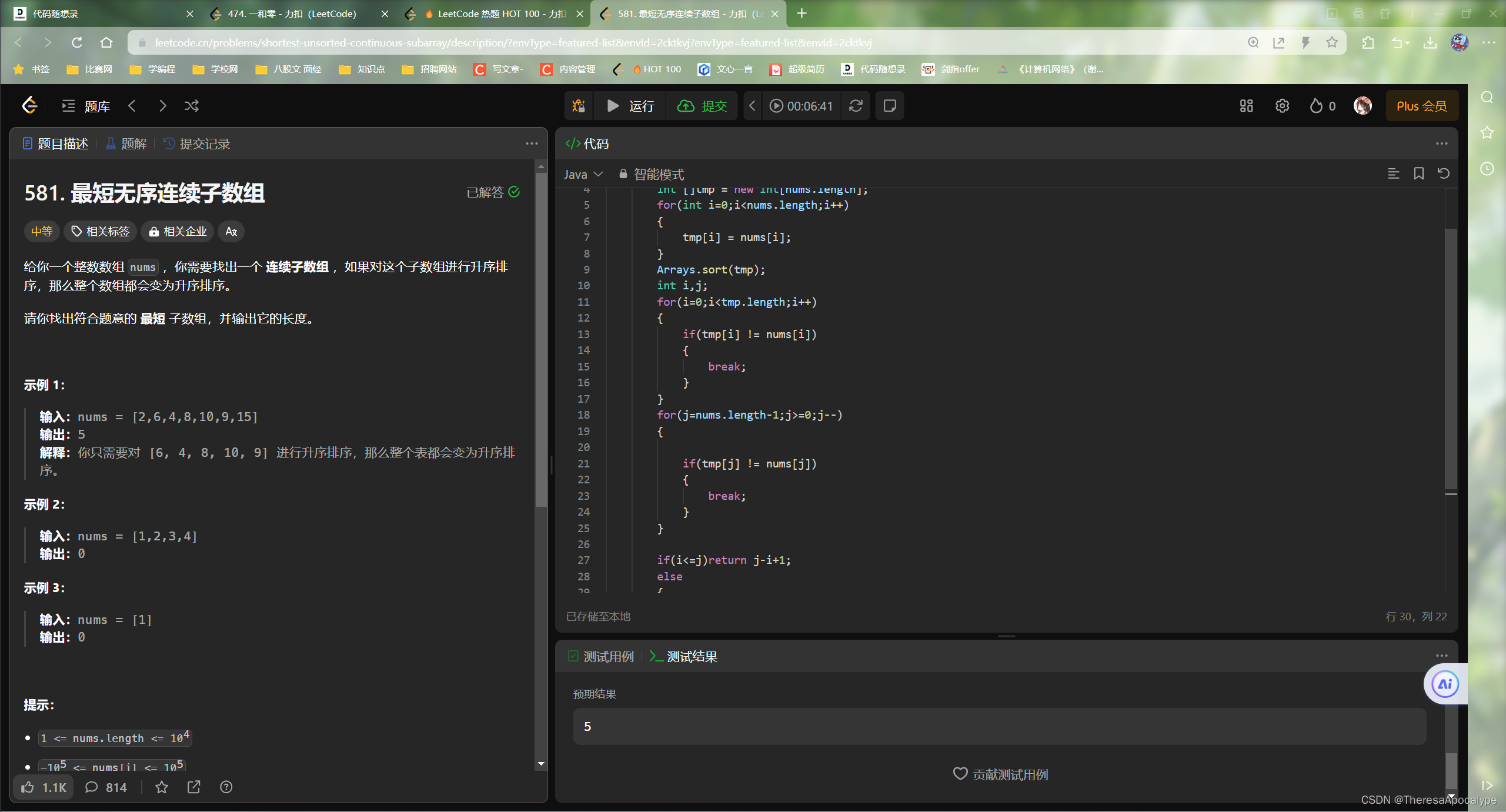
12.31

209. 长度最小的子数组

思路：滑动窗口，先不断右移直到sum>=target ，然后左指针左移直到小于target，记录暂时的最小长度，然后继续右移右移直到sum>=target ，左指针左移直到小于target，不断迭代最小长度

和为 K 的子数组

使用前缀和，核心是

map.containskey(sum-k);
map.put(sum,map.getOrDefault(sum,0)+1);

滑动窗口

按照这题为模板

这种题的特征是 "子串" "子数组" 这种需要连续元素的

有一个窗口在扫描，使用两个变量left限制左范围：right用于for遍历计数

tmp,max用于记录最终数据

从0处开始滑动区间，right每加一次，就判断right这个元素和窗口内的元素是否满足某种条件

如果不满足了就进入处理块, 不断把left向右推进直到他满足条件, 在外层循环记录tmp和最大的max即可.(此题判断的条件是是否有重复元素，有就把left推进到重复的位置)

无重复字符最长子串

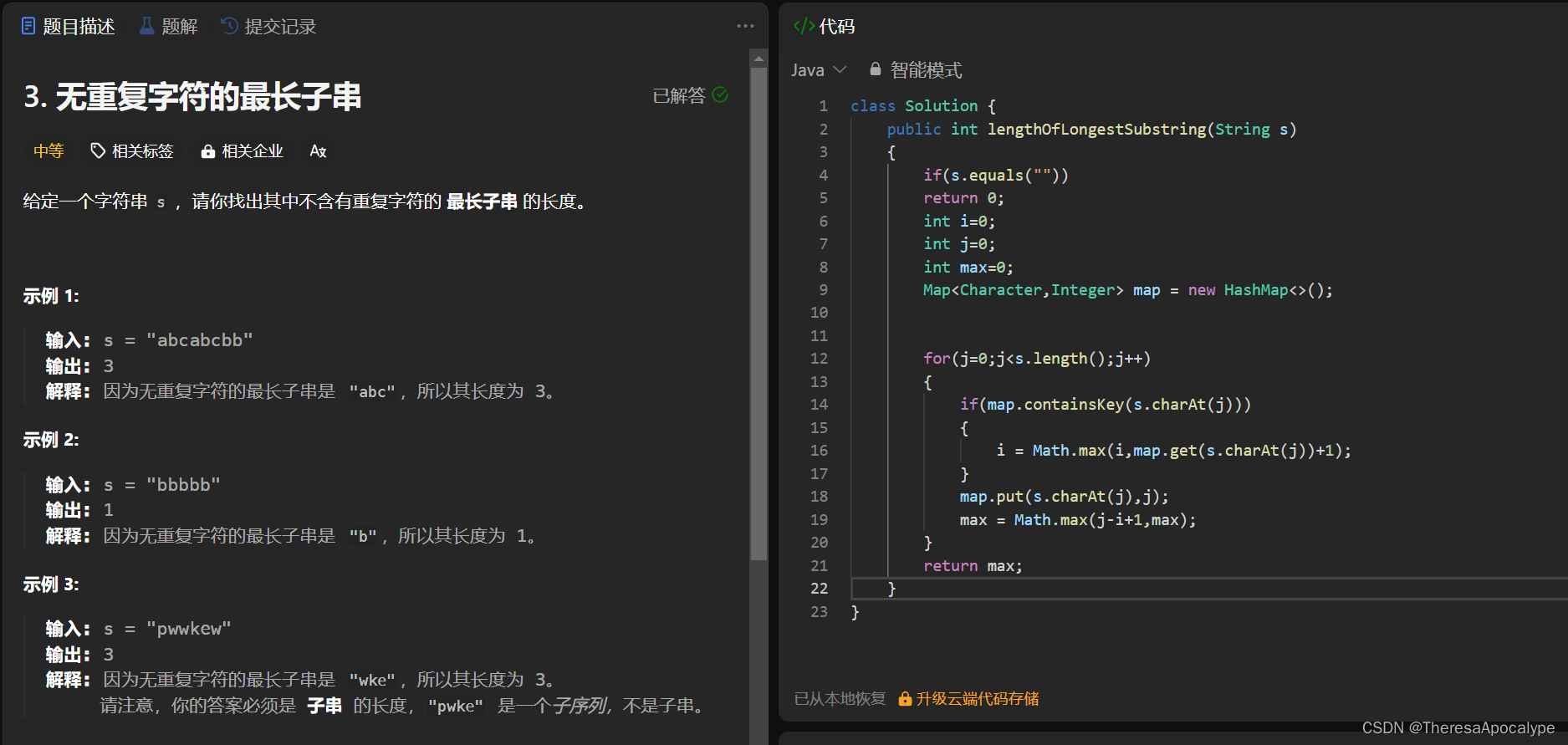
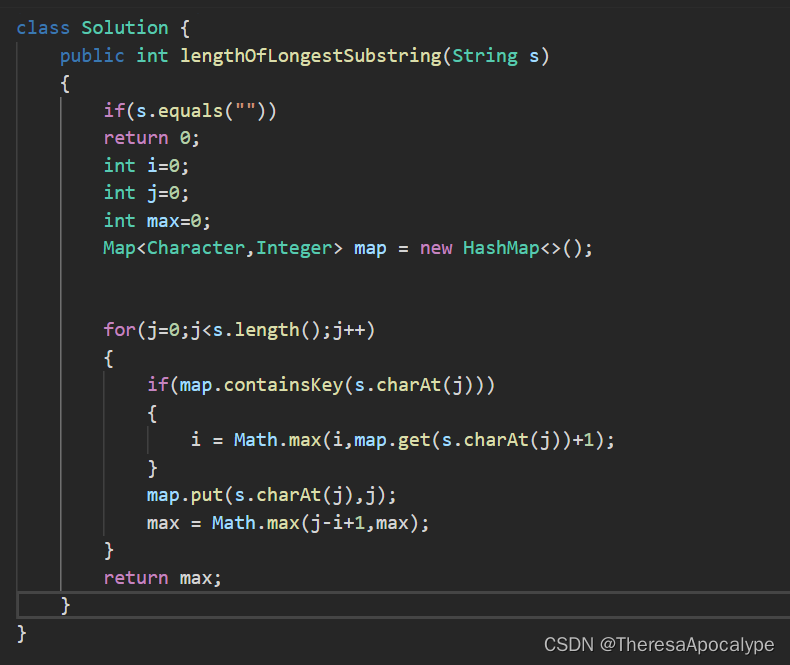
字节最经典的一道题

注意要用HashMap提高查找效率

containsKey先于put处理防止自己contains自己。调整i位置，通过比较两个元素下标谁大，来确定谁是后面的0
左边界调整位置的时候调整到第一个有效位（即重复位+1），而不是重复位，因为如果这个字符串没有重复的，此时应该使用j-i+1计算结果，然而如果是调整到重复位结果就变成了j-i，没有统一。所以必须挪到重复位的右边(第一个有效位)！
i = Math.max(i,map.get(s.charAt(j))+1); 这一句是比较当前边界和重复字符谁更右，

取更右边的作为边界

重点：要用HashMap来搞。注意put是会覆盖相同的元素的！！！！由于遍历的顺序是下标由小到大，因此得到的那个重复元素的下标一定是目前最大的，直接和左边界比较即可

哈希表(12.9-12.16)

什么时候使用哈希法:

1.当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

经典题: 比较两个集合的元素重叠的地方, 或者这个数组能不能由那个数组里的元素构成

2.当我们需要在一次遍历中记录某种元素出现的次数, 或者记录某个和他相关的特征的时候

抽象来说就是, 需要建立一个数据和另一个数据之间的映射关系的时候

下面是这两种数据结构的一些常用方法：

HashMap

put(key, value): 如果key已经存在，那么值就更新
get(key): 根据key获取value
remove(key): 删除HashMap中指定key的元素
containsKey(key): 检查HashMap中是否包含给定的key
containsValue(value): 检查HashMap中是否包含给定的value
keySet(): 返回所有key的Set
values(): 返回所有value的Collection
isEmpty(): 检查是否为空
clear(): 清除所有元素
map.put(i , getOrDefault(map.get(i),0)+1)

HashSet

add(element): 添加一个元素
remove(element): 删除一个元素
contains(element):是否包含给定的元素
isEmpty(): 检查是否为空
clear(): 清除所有元素
size(): 返回元素的数量
iterator(): 返回一个迭代器，用于遍历HashSet中的所有元素。

回溯(12.19-12.24)

为什么要用回溯?

for循环只能有单层遍历,但是回溯是可以多层遍历
回溯的本质就是多层遍历, 用for循环控制这一层的广度, 用递归控制深度, 用退出条件控制结束时机
一定要画图辅助理解,可以明确写递归方法的思路, 这很重要
什么题用回溯?问你返回所有可能得什么什么组合,集合, 需要枚举/遍历所有情况 , 特别是组合/子集问题,要从题目抽象中出来

基本步骤

定义结果res集合(ArrayList) 临时存储tmp集合(LinkedList) 当前总和int sum

    List<List<Integer>> res = new ArrayList<>();
    List<Integer> tmp = new LinkedList<>();
    int sum=0;

定义dfs函数, 包含传入的数组nums, 每次遍历的开头begin, 目标target
定义退出条件: 等于target时把tmp加入res然后返回超出target直接返回大小超出也返回
定义循环体:注意for(i=begin;i<length;i++)

 tmp.add(candidates[i]);
    sum += candidates[i];
    dfs(candidates, i ,target);
    sum -= candidates[i];
    tmp.removeLast();

三大要点总结

数组中(有无)重复元素
结果中(能否)含有重复元素
结果(能否)出现重复集合(顺序不同是否算同一个集合)

主要是修改i = begin参数和 dfs(nums, i ,target)中是 i 还是 i+1

子集能重复, 只用修改为 i=0 不可重复则是 i=begin

重点情况:

数组中无重复元素结果中不能含有重复元素子集不能出现重复:

i=begin dfs(nums, i+1 ,target)
数组中有重复元素结果中能含有重复元素子集不能出现重复:

加条件:

if(i > begin && nums[i] == nums[i-1]) continue;

i=begin dfs(nums, i+1 ,target)
数组中有重复元素结果中不含有重复元素子集不能出现重复:

加条件:

if(i > 0 && nums[i] == nums[i-1]) continue;

i=begin dfs(nums, i+1 ,target)

###

回文子串问题

12.28

class Solution {
    List<List<String>> res = new ArrayList<>();
    List<String> tmp = new LinkedList<>();
    public List<List<String>> partition(String s) 
    {
        int index = 0;
        dfs(0,s);
        return res;
    }

    public void dfs(int index , String s)
    {
        if(index == s.length())
        {
            res.add(new ArrayList(tmp));
        }

        for(int i = index;i < s.length();i++)
        {
               if(fun(index,i,s) == true) 
               {
                   String now = s.substring(index,i+1);
                   tmp.add(now);
                   dfs(i+1,s);
                   tmp.removeLast();
               }
        }
    }

    public boolean fun(int i,int j,String s)
    {
        while(true)
        {
            if(i >= j)return true;
            if(s.charAt(i) != s.charAt(j))
            {
                return false;
            }
            i++;
            j--;
        }
       
    }



}

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

可以算困难一级的了

难点:

把分割方案化为回溯问题, 我们想枚举每一种字符串的分割方式, 再一个一个去验证
可以看做是字符间空隙的组合问题(在一个空隙集合中选择不同的空隙组合) 采用回溯枚举
因为for循环只能有单层遍历,但是回溯是可以多层遍历(回溯的本质就是遍历, 用for循环控制这一层的广度, 用递归控制深度, 用退出条件控制结束时机 )
一定要画图辅助理解, 这很重要,一开始都没意识到
判断回文直接双指针

//我们使用index来代表当前遍历的空隙, 当枚举到**最后一个字符后**的空隙时就才遍历
if(index == s.length())  
        {
            res.add(new ArrayList(tmp));
        }

        for(int i = index;i < s.length();i++)
        {
 //index和i表示我们当前处理的哪两个空隙之间的字符串,只有当前满足是回文我们才继续去dfs,否则直接进入下一个循环,这样保证了只有回文, 并且因为只有遍历到最后一个字符后才会结束,所以不用担心会脏结果
               if(fun(index,i,s) == true) 
               {
                  String now = s.substring(index,i+1);  //注意边界是[index,i]
                   tmp.add(now);
                   dfs(i+1,s);//从下一个字符开始继续判断
                   tmp.removeLast();
               }
        }

动态规划(12.25-1.4)

如果某一问题有很多重叠子问题，使用动态规划是最有效的。

就是你发现这一步的答案要根据上一步的答案得，而且上一步的答案也是同样的方法得到的

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的

状态转移公式（递推公式）是很重要，但动规不仅仅只有递推公式。

动规五步曲（一定要明确的每一步结果写出来）

确定dp数组（dp table）以及下标的含义

这很重要，注释出来
确定递推公式

写完dp数组含义以后立马着手递推公式用注释先写上
dp数组如何初始化

一定要注意dp[0] dp[1] 这种边界值的初始化，很有可能要取特值
确定遍历顺序

要确保后面的可以由前面的推出来，特别是多维dp
举例推导dp数组

为什么要先确定递推公式，然后在考虑初始化呢？因为一些情况是递推公式决定了dp数组要如何初始化！

Debug三问

这道题目我举例推导状态转移公式了么？
我打印dp数组的日志了么？
打印出来了dp数组和我想的一样么？

背包问题

01背包

（1）

对于背包问题，有一种写法即dpi 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

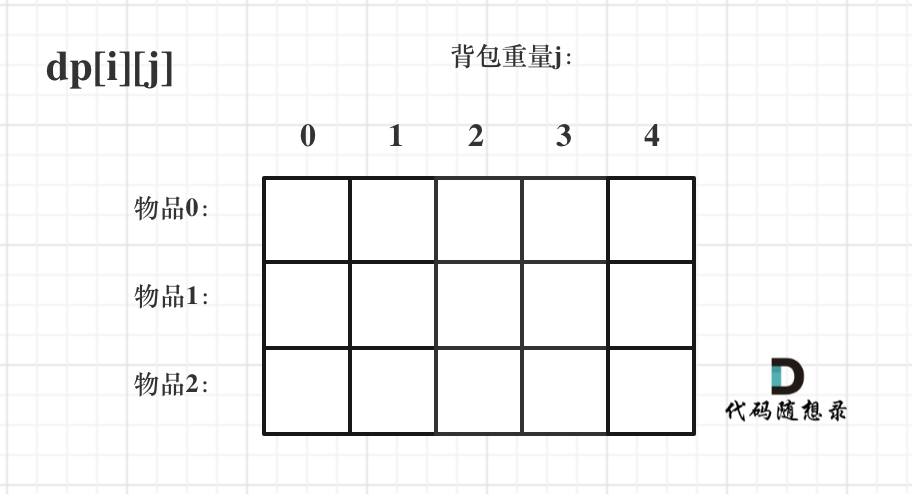
动态规划-背包问题1

确定递推公式

不放物品i：和上一个相同。由dp[i - 1] [j]推出，即背包容量为j，里面不放物品i的最大价值，此时dpi就是dp[i - 1] [j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)

放物品i：等于上一个加这个的value。由dp[i - 1] [j - weight[i]]推出，dp[i - 1] [j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1] [j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

取i那就是后者，不取i就是前者

dp[i][j] = max{ dp[i-1][j] , dp[i-1][j-weight[i]] + value[i] }

（2）滚动数组法

重点一定要记住，就是数据的覆盖

在此时，数组是一遍一遍覆盖的。覆盖前就相当于原来的dp[i-1 ] [j ],所以此时，不取物品i 的情况就可以化为dp[j ] 直接就是上一个的。同理，要取物品i 就直接化为dp[j-weight ]+value[j ]

dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]

初始化dp就应该全是0，在题目给的全是正整数的情况下可以保证后续被覆盖掉。

循环还是双重循环，要有i 控制前n个物品进不进去，但是dp会减少一维度

同时我们可以窥见遍历的次序问题。因为我们要保证j 之前的数据还没有被覆盖

因为有比较dp[j - weight[i]] + value[i]的部分

所以我们要倒序遍历

ps：能不能交换遍历顺序？不能，不然就变成 dp[j]表示：取前 j 个的背包，所背的物品价值可以最大为dp[j]