一、基本概念
静态查找:只查找,不改变集合内数据元素
动态查找:有则输出元素,无则添加元素
二、静态查找表
2.1顺序查找
在线性表、链表、树中依次查找
2.2折半查找(二分查找)
在有序的线性表中,每次都与中间位置元素进行比较,根据大小向左或向右缩小查找区域
#include<stdio.h>
#include<stdlib.h>
//void search(int l[], int low, int high, int value) //二分查找递归版
//{
// if (high < low)
// return;
// int mid = (low + high) / 2;
// if (l[mid] == value)
// {
// printf("第%d个", mid+1);
// return;
// }
// if (l[mid] < value)
// search(l, mid, high, value);
// else
// search(l, low, mid, value);
//}
int search2(int* l, int n, int target) //二分查找非递归版
{
int low = 0, high = n - 1, mid;
while (low <= high) //相等时还可以比较一次
{
mid = (low + high) / 2;
if (target == l[mid])
return mid;
else if (target < l[mid])
high = mid - 1;
else
low = mid + 1;
}
return -1; //不能return0
}
int main() {
int l[10] = { 1,2,3,4,5,6,7,8,9,10 };
//search(l, 0, 9, 9);
printf("%d", search2(l, 10, 3));
}折半查找的ASL
第一趟能比较一个元素,第二趟能比较两个元素,第三趟能比较三个元素……
总共查找次数为1*1 + 2*2 + 3*4 + 4*8+……当比较过的总元素等于表中关键字个数位置
ASL=总次数/总个数
具有12个关键字的有序表,折半查找的平均查找长度( )
答案:(1*1 + 2*2 + 3*4 + 4*5)/ 12 = 3.1 (最好写成小数形式)
在有序线性表a[20]上进行折半查找,则平均查找长度为()
答案:3.7
(多选题)使用折半查找算法时,要求被查文件()
A.采用链式存贮结构 B.记录的长度≤12 C.采用顺序存贮结构 D.记录按关键字递增有序
答案:CD
折半查找失败的平均查找长度
构建二分查找树
第一次找到(1+12)/2=6,6就为第一个节点。如果向左,(1+5)/2=3为左孩子。如果向右,(7+12)/2=9为右孩子,如此把节点都放入树中。
补上所有空节点(图中绿色方块),这就是查找失败的位置。
失败的平均次数=求和(根节点到失败节点经过的边数)/失败节点个数
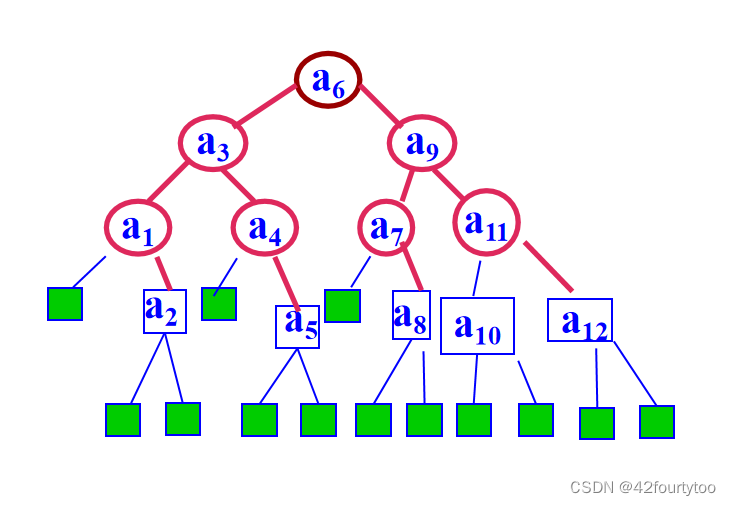
具有12 个关键字的有序表中,对每个关键字的查找概率相同,折半查找查找成功和查找失败的平均查找长度依次为( )
答案: 37/12,49/13
2.3分块查找
让数据分成若干子表,子表内不必有序,但要求每个子表中的数据元素值都比后一块中的数值小。然后将各子表中的最大(或最小)关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针)。
特点:块间有序,块内无序
查找:块间折半,块内线性

三、二叉排序树
定义:左子树的所有结点均小于根的值,右子树的所有结点均大于根的值;它的左右子树也分别为二叉排序树。
分别以下列序列构造二叉排序树,与用其它三个序列所构造的结果不同的是()
A.100,80, 90, 60, 120,110,130
B.100,120,110,130,80, 60, 90
C.100,60, 80, 90, 120,110,130
D.100,80, 60, 90, 120,130,110
答案:C 按照左小右大进行插入
查找:与节点比大小,往左右走;当查不到时,新建节点
node* newnode(int v) { //新建节点,返回地址
node* newnode = (node*)malloc(sizeof(node));
if (!newnode) return NULL;
newnode->data = v;
newnode->lchild = NULL;
newnode->rchild = NULL;
return newnode;
}
void insert(pnode& root, int value) { //递归寻找,定位到值该在的位置
if (root == NULL) {
root = newnode(value);
return;
}
if (root->data > value)
insert(root->lchild, value);
else
insert(root->rchild, value);
}删除节点:
节点是叶子:直接删
节点一个孩子:删掉节点,把孩子接上去
节点两个孩子:用左子树最大值或右子树最小值覆盖该节点,然后删去左子树最大值或右子树最小值
四、平衡二叉树
每个节点有一个平衡因子,它等于左子树高度 - 右子树高度
任一结点的平衡因子只能取:-1、0 或 1的树为平衡二叉树
4.1平衡旋转
插入节点导致不平衡,要进行旋转
无论哪种情况,都从最下层不平衡节点开始处理
LL型:从不平衡点开始,沿着失衡路径的下一个节点要变为新的根节点,他的孩子和父亲变为左右节点
RR型:同LL
LR型:新节点先不插入。不平衡节点的下二层节点要变为新的根,他的上面两代节点做他的左右孩子,其他节点照抄,再插入新节点
RL型:同LR
五、哈希表
哈希表是散列存储结构,由关键码的值决定数据的存储地址。查找效率O(1),与元素个数无关
冲突:由于hash函数自身存在的问题,因而经过哈希函数变换后,可能将不同的关键码映射到同一个哈希地址上,这种现象称为冲突。
装填(载)因子:a=n/m ,其中n 为关键字个数,m为表长。 装填(载)因子是表示Hsah表中元素的填满的程度。若:装载因子越大,填满的元素越多,好处是,空间利用率高了,但:冲突的机会加大了。反之,装载因子越小,填满的元素越少,冲突的机会减小了,但空间浪费多了。冲突的机会越大,则查找的成本越高,反之查找时间越小。
5.1哈希函数构建
除留余数法
Hash(key) = key mod p (p是整数)
以关键码除以p的余数作为哈希地址
p的选取:若设计的哈希表长为m,则一般取p≤m且为质数
5.2冲突处理方法
线性探测法
有冲突时,向后寻找下一个空的地址,将元素存入
二次探测法
有冲突时,按照1,-1,4,-4……的次序寻找(全是平方,正负交替)
链地址法
建立一个从0到p-1的指针数组,把对应的元素链接到后面
设{ 47, 7, 29, 11, 16, 92, 22, 8, 3, 50, 37, 89 ,10}的哈希函数为:Hash(key)=key mod 11, 用拉链法处理冲突,如下图

5.3ASL
顺序表:
哈希表查找成功的平均查找长度:查找每个元素所需的对比次数求和,除以元素数
哈希表查找失败的平均查找长度:设取余数时模m。则在哈希表0~m-1号元素中,每一位查找到空元素所需要的次数求和,除以m
链表:
查找成功的平均查找长度:纵向来看,第i层元素数*i求和/元素数
查找失败的平均查找长度:横向来看,每一行查到空元素的对比次数求和/总行数
六、B树
B树是一种 m叉 平衡 排序树
1.每个节点的子树数=关键字数+1
2.根节点关键字为1~m-1
3.非根节点中关键字个数为~m-1
4.非根节点中子树个数为~m
三阶B树关键字数:1~2;五阶B树关键字数:2~4
5.所有的叶子结点都出现在同一层次上,并且不带信息(实际上不存在,指向这些节点的指针为空)
在一棵高为2 的5阶B树中,所含关键字的个数最少是()
答案:5 根节点最少一个,则有两个子树,非根节点最少两个,1+2+2=5
在一棵具有15个关键字的4阶B树中,含关键字的结点数最多为()
答案:15 4阶B树关键字1~3,每个节点一个关键字时节点最多
B树插入
根据大小将插入节点放到合适的区域;如果该区域超出m-1,将中间一位数上移,左右分裂
B树删除
删除叶子节点:删了不满足下限要求的时候,若兄弟有富余,删除数据后通过旋转向兄弟借;若兄弟无富余,不论父节点如何,父节点数据下移,与左右孩子节点合并。(当一个节点内无数据时,要当作数据为0的节点,不是没有节点)
删除非叶子节点:用左子树最大值进行替换,对不符合要求的节点进行删除叶子节点后同样的处理。
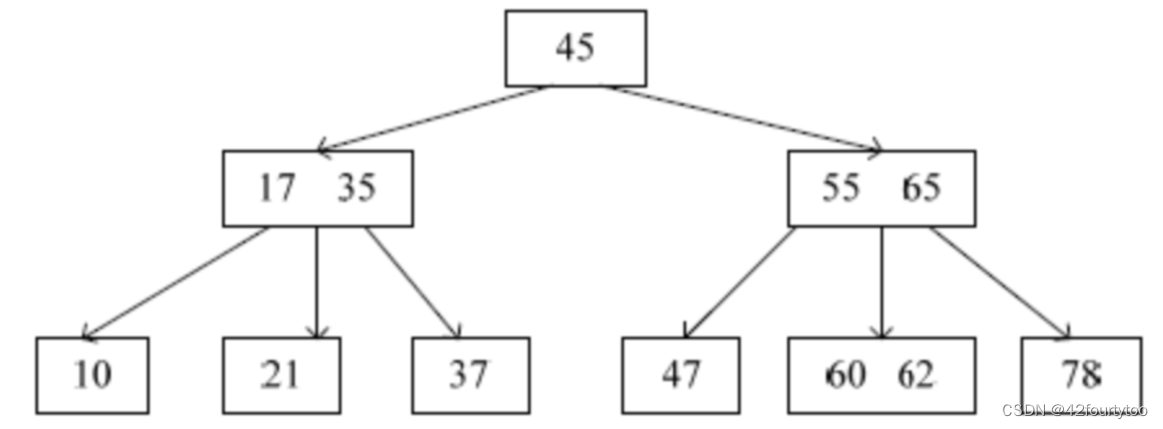
已知一棵3阶B树,如下图所示。删除关键字78得到一棵新B树,其最右叶结点中的关键字是( )
答案:65 兄弟有,从兄弟借