目录
- 引言
- 一、最大异或对(Trie树扩展)
- 1.题目描述
- 2.解题思路
- 3.代码实现
- 4.测试
- 二、食物链(并查集扩展)
- 1.题目描述
- 2.解题思路
- 3.代码实现
- 4.测试
引言
这两个扩展题能够让我们更加的熟悉Trie树和并查集的使用,这两道题可以说是比较难的了,所以说还是好好对待吧。
一、最大异或对(Trie树扩展)
1.题目描述
在给定的 N 个整数 A1,A2……AN 中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N。
第二行输入 N 个整数 A1~AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤105,0≤Ai<231
输入样例:
3
1 2 3
输出样例:
3
2.解题思路
- 首先最开始当然是用暴力做一下,如下所示,很明显是O(n^2)的一个时间复杂度,然后这个数据是10 ^ 5,那就是执行10 ^ 10次,然后一般C++的时间范围在10 ^ 9内一般都是可以过的,这个当然就TLE了。
int res = 0;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < i; ++j)
{
res = max(res, a[i] ^ a[j]);
}
}
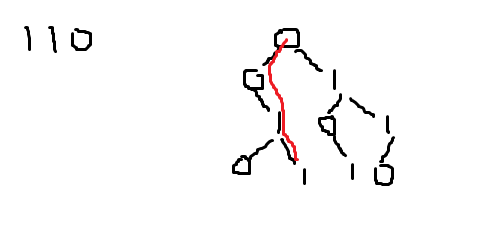
- 然后就想怎么优化了,我们注意第二层循环是查找当然数中与a[i]异或的最大值,我们发现数据是小于 2 ^ 31 - 1的,也就是最多31位,那么是最大的,肯定先从最高位找有没有一个数跟a[i]的最高位不一样,如果有那就把他们集合到一块,没有那就挑相同的,然后找第29位有没有与a[i]第29位不同位的树,如果没有那就找相同的,然后就这样找到第0位,肯定就是与a[i]异或最大的数了,这也是一种贪心的思想,具体图解看如下的例子:
如果右边是已经有的Trie树了,我们要找与110异或最大的,那么最高位是1,我们就要找0,然后有0,然后看下一位是1,我们就要找0,没有0,那就只能是1了,然后下一位是0,我们要找1,那就找到了,所以最终与110异或最大的数是011
3.代码实现
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 1e5+10, M = 31 * N; // 最大有M个结点
int a[N];
int son[M][2], idx; // M个结点,每个结点两个儿子0,1
int n;
void insert(int x)
{
int p = 0;
for(int i = 30; i >= 0; --i)
{
int u = x >> i & 1;
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
}
int query(int x)
{
int p = 0, res = 0;
for(int i = 30; i >= 0; --i)
{
int u = x >> i & 1;
if(son[p][!u]) // 找不同的
{
res = res * 2 + !u;
p = son[p][!u];
}
else // 如果不存在,那只能退而求其次
{
res = res * 2 + u;
p = son[p][u];
}
}
return res;
}
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; ++i) scanf("%d", &a[i]);
int res = 0;
for(int i = 0; i < n; ++i)
{
insert(a[i]);
int t = query(a[i]); //查询与a[i]异或最大的数
res = max(res, a[i] ^ t);
}
printf("%d\n", res);
return 0;
}
4.测试

二、食物链(并查集扩展)
1.题目描述
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N 编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话;
当前的话中 X 或 Y 比 N 大,就是假话;
当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行是两个整数 N 和 K,以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000 ,0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
2.解题思路
这道题是要输出谎话的次数,然后x,y > n,就不说了很好判断,然后其实就是判断是不是同类,是不是能吃的关系
思路就是如下图的关系,是不是同类取决于到根结点的距离是否相同,吃与被吃的关系却决于到根结点的距离,当然这些距离都要 mod 3
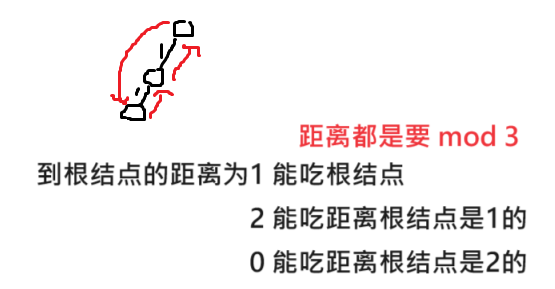
3.代码实现
关于最后 d[px] 的推导我画了张图,虽然很丑,但是关系描述的还是很清晰的,然后注释写的也比较详细,不懂得可以多看看


#include <cstdio>
#include <iostream>
using namespace std;
const int N = 5e5+10;
int p[N], d[N]; // d[i]是i号结点到根结点的距离
int n, m;
int find(int x)
{
if(x != p[x])
{
int t = find(p[x]);
d[x] += d[p[x]]; // 必须先执行find操作,将d[p[x]是真正的到根结点的距离,而不是到上一个结点的距离
p[x] = t; // 路径压缩
}
return p[x];
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) p[i] = i;
int res = 0;
while(m--)
{
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
int px = find(x), py = find(y);
if(x > n || y > n) res++;
else
{
if(t == 1) // 同类
{
if(px == py && (d[x] - d[y]) % 3) res++; //如果是一个集合的,并且到根结点的距离不同,说明不是一个类的
else if(px != py) // 刚开始还没插进集合里
{
p[px] = py; // 让x的根结点的父亲为y的根结点
d[px] = d[y] - d[x]; // 只用将x根结点到y根结点的距离一改,之后的话,会通过上面的find函数自动修改的
}
}
else // x吃y
{
int link = 1; // 这里给出2也是可以的,x比y多1或者2 都表示x吃y
if(px == py && (d[x] - d[y] - link) % 3) res++;
else if(px != py)
{
p[px] = py;
d[px] = d[y] - d[x] + link;
}
}
}
}
printf("%d\n", res);
return 0;
}
4.测试