原理
二维傅里叶变换是一种在图像处理中常用的数学工具,它将图像从空间域(我们通常看到的像素排列)转换到频率域。这种变换揭示了图像的频率成分,有助于进行各种图像分析和处理,如滤波、图像增强、边缘检测等。
在数学上,二维傅里叶变换的原理可以描述如下:
基本概念:
空间域:图像以像素的形式展示,每个像素表示特定位置的亮度或颜色值。
频率域:图像表示为不同频率的波形组合。在这个域中,图像的每个点表示一个特定频率的振幅和相位。
变换过程:
二维傅里叶变换通过将图像从空间域转换到频率域,揭示了图像中的频率信息。
变换公式涉及复数运算,考虑图像中每个点对所有频率成分的贡献。
数学表达式:
对于一个二维图像 f(x,y),其傅里叶变换
F(u,v) 定义为:
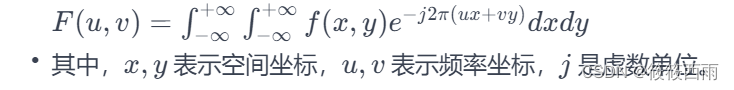
应用:
在频率域,图像的不同特性(如边缘、纹理)会表现为不同的频率成分。
对频率域的操作(如滤波)后,可以通过逆傅里叶变换将图像恢复到空间域。
直观理解:
低频成分通常对应于图像中的大面积均匀区域。
高频成分对应于图像中的细节,如边缘和纹理。
二维傅里叶变换在图像处理中的应用广泛,是一种强大的工具,能够帮助理解和处理图像信息。
python代码实现

提示
函数np.fft.fft2可以得到其傅里叶变换系数,用np.abs计算复数幅度谱后显示如右上图 所示。经对数变换后显示如左下图。最后经np.fft.fftshift函数将频谱图中心化。生成更多图像,比如单频率正弦波图像,观察它们的频谱成分。
代码
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('cameraman.tif', 0)
#img = cv2.imread('Fig0421.tif', 0)
dft = np.abs(np.fft.fft2(img))
log_dft = np.log(1+dft)
center_dft = np.fft.fftshift(log_dft)
img_list = [img, dft, log_dft, center_dft]
img_name_list = ['original', 'DFT', 'log transformed DFT', 'centralized DFT']
_, axs = plt.subplots(2, 2)
for i in range(2):
for j in range(2):
axs[i, j].imshow(img_list[i*2+j], cmap='gray')
axs[i, j].set_title(img_name_list[i*2+j])
axs[i, j].axis('off')
plt.savefig('2D_FFT.jpg')
plt.show()
结果展示

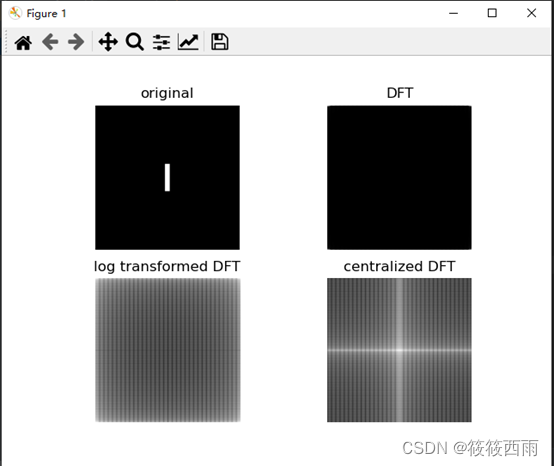
结果分析
傅里叶谱图上的每一个像素点都代表一个频率值,幅值由像素点亮度变码而得。最中心的亮点是指直流分量,傅里叶谱图中越亮的点,对应于灰度图中对比越强烈(对比度越大)的点。
实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。
对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰.
图像信号能量将集中在系数矩阵的四个角上。经过变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大。