复试 || 就业day01(2023.12.29)项目一

news2024/11/23 6:39:00

文章目录

前言
正规方程
二元一次示例
正规方程 : $w = (X^TX)^{-1}X^Ty$
三元一次方程示例
八元一次方程示例
sklearn
带截距的线性方程
总结

前言

💫你好，我是辰chen，本文旨在准备考研复试或就业
💫本文内容来自某机构网课，是我为复试准备的第一个项目
💫欢迎大家的关注，我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块，需掌握基本Python语法, Numpy, Pandas, Matplotlib

以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新)，欢迎大家的关注：

💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解

正规方程

二元一次示例

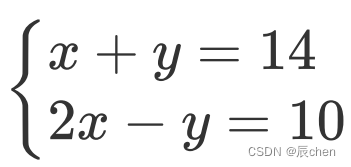
在这里插入图片描述

import numpy as np
X = np.array([[1, 1], [2, -1]])
y = np.array([14, 10])

# np.linalg : 线性代数, .solve : 解决线性回归问题
np.linalg.solve(X, y)   # 效果和 LinearRegression 是等同的,默认也是计算不带截距

在这里插入图片描述

正规方程 : $w = (X^TX)^{-1}X^Ty$

A = X.T.dot(X)   # 计算 X^T · X
B = np.linalg.inv(A) # 计算 A^(-1 )
C = B.dot(X.T)
C.dot(y)

在这里插入图片描述

三元一次方程示例

在这里插入图片描述

X = np.array([[1, -1, 1], [2, 1, -1], [3, -2, 6]])
y = np.array([100, 80, 256])
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y) # 正规方程
print(w)

在这里插入图片描述

八元一次方程示例

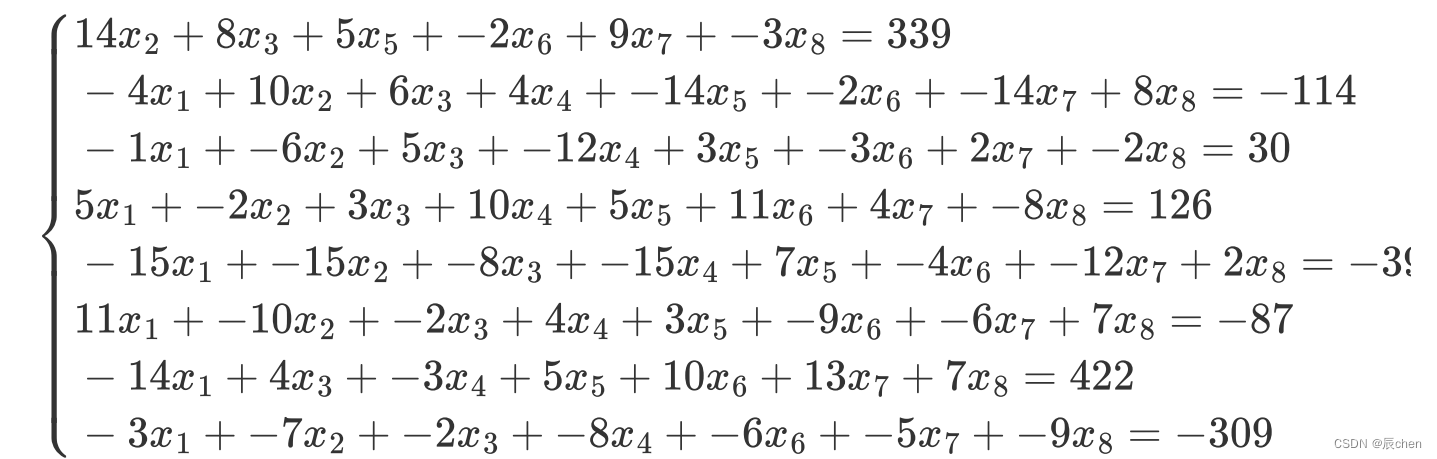
在这里插入图片描述

X = np.array([[0, 14, 8, 0, 5, -2, 9, -3],
              [-4, 10, 6, 4, -14, -2, -14, 8],
              [-1, -6, 5, -12, 3, -3, 2, -2],
              [5, -2, 3, 10, 5, 11, 4, -8],
              [-15, -15, -8, -15, 7, -4, -12, 2],
              [11, -10, -2, 4, 3, -9, -6, 7],
              [-14, 0, 4, -3, 5, 10, 13, 7],
              [-3, -7, -2, -8, 0, -6, -5, -9]])
y = np.array([339, -114, 30, 126, -395, -87, 422, -309])
w = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)
print(w)

在这里插入图片描述

sklearn

# linear model : 线程方程
# LinearRegression : 线性回归
from sklearn.linear_model import LinearRegression

model = LinearRegression()

# X : 数据, y : 目标值
display(X, y)
model.fit(X, y)

# coef_ : 结果,返回值,系数,斜率,方程的解
model.coef_

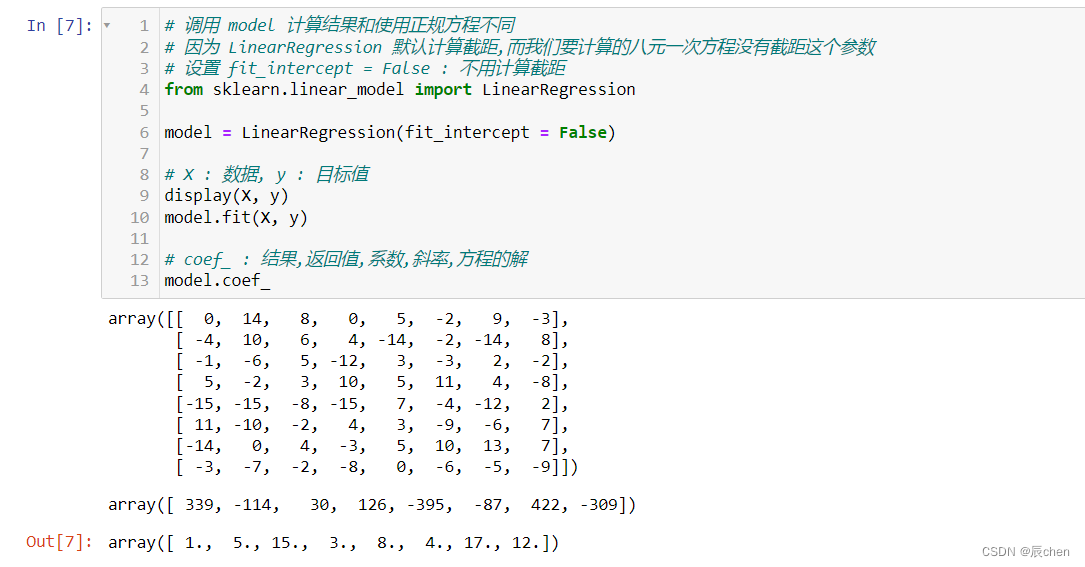
在这里插入图片描述

# 调用 model 计算结果和使用正规方程不同
# 因为 LinearRegression 默认计算截距,而我们要计算的八元一次方程没有截距这个参数
# 设置 fit_intercept = False : 不用计算截距
from sklearn.linear_model import LinearRegression

model = LinearRegression(fit_intercept = False)

# X : 数据, y : 目标值
display(X, y)
model.fit(X, y)

# coef_ : 结果,返回值,系数,斜率,方程的解
model.coef_

在这里插入图片描述

带截距的线性方程

# 默认 axis = 0, 表示纵向拼接(多一行), axis = 1 表示横向拼接(多一列)
# np.full : shape(8, 1) : 8行1列  ;  fill_value : 填充值 
X = np.concatenate([X, np.full(shape = (8, 1), fill_value = 1)], axis = 1)
# 设 X 的每一行都添加了一个截距 12, 同样 y 也得跟着变换
y += 12  # 增加一列 12 的截距
# 需注意，我们是知道截距=12，但是计算机是不知道的，它会将12当成一个未知参数去计算
# 那么就相当于变成了九元一次方程组，若想出唯一解，我们需要至少九个方程
display(X, y) # 此代码块只能执行一次，每执行一次会添一列 1

在这里插入图片描述

# 增加一个方程
w = np.array([ 1.,  5., 15.,  3.,  8.,  4., 17., 12.]) # 这是标准答案
display(w)

# 随机生成 8个数作为第九个方程的xi
# 生成长度为8的一维数组,数组元素为 [-15, 15)
X9 = np.random.randint(-15, 15, size = 8) 
display(X9)

#新添加的方程也需要添加 12
y = np.concatenate([y, [X9.dot(w) + 12]])

# 给 X9 增加一列 1，并添加到 X 中
X9 = np.concatenate([X9, [1]])
display(X9)
X = np.concatenate([X, [X9]])
display(X)

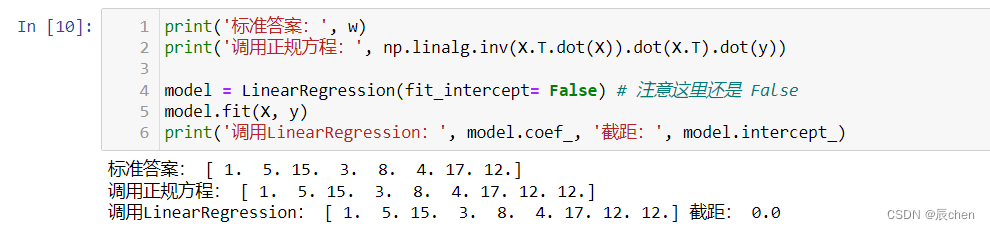
在这里插入图片描述

print('标准答案：', w)
print('调用正规方程：', np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y))

model = LinearRegression(fit_intercept= False) # 注意这里还是 False
model.fit(X, y)
print('调用LinearRegression：', model.coef_, '截距：', model.intercept_)

在这里插入图片描述

model = LinearRegression(fit_intercept= True) # 注意这里更改为了 True
# 即让计算机去计算截距 12，所以求得的 x9 的值为 0
model.fit(X, y)
print('调用LinearRegression：', model.coef_, '\n截距：', model.intercept_)

在这里插入图片描述

model = LinearRegression(fit_intercept= True) # 注意这里更改为了 True
# 把截距这一列去掉（不当成参数）(x9 == 0 没有什么意义)
model.fit(X[:,:-1], y)
print('调用LinearRegression：', model.coef_, '\n截距：', model.intercept_)

在这里插入图片描述

总结

在这里插入图片描述
调用 np.linalg.solve(X, y) 和调用 LinearRegression 计算正规方程是一个效果，np.linalg.solve(X, y) 也是默认的不计算截距

说一下最后的添加截距（拿上述八元一次方程组举例），首先调用 LinearRegression 默认的 fit_intercept 为 True 即为计算截距，如果我们本身方程没有截距，那么计算的结果就会有出入。

第一种方法：仍写成：fit_intercept= False 我们对于添加截距相当于要额外添加一列，需要对参数方程额外添加一列 1 ，但是计算机是不知道我们自己添加了一列的，只会把多出来的这一列当作新的未知变量，即方程变成了九元一次方程，这时候只有八个方程，故欲确定唯一解，我们需要自己补一行方程，注意这种方法解出来其实仍然是没有截距的（计算机把截距当成了一个新的未知数），所以调用 model.intercept_ 查看斜率仍然是 0，解得的新参数 X9 的值为 12；
第二种方法：写成 fit_intercept= True 即把新添加进来的视为截距，那么就没有必要再添加额外的一列未知量 1 了，添加的话则会解得 X9 的值为 0 代表 X9 无权（没用），调用 model.intercept_ 查看斜率则为 12.000000000000007 舍入后得 12