Beta分布与二项分布的关系
Beta分布与二项分布密切相关,由二项分布扩展而来,它是用来描述一个连续型随机变量出现的概率的概率密度分布,表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) , a 、 b a、b a、b 是形状参数。Beta分布本质上也是一个概率密度函数,只是这个函数的自变量和因变量都表示某种概率。
下面我们会先温故下二项分布的知识,然后循序渐进地引出Beta分布。
在二项分布这篇文章里介绍过,二项分布能解决的是 n次独立伯努利试验中成功k次的概率 问题,记作 X X X~ B i n ( n , p ) Bin(n,p) Bin(n,p) 。
仍以抛硬币为例,二项分布求的是抛 n n n 次硬币中出现 k k k 次正面向上的概率,它是一个概率质量函数(对离散型随机变量叫概率质量函数、对连续性随机变量叫概率密度函数),这个函数的自变量是 k k k ,因变量是概率,前提是硬币出现正面向上的概率 p p p (质地均匀)和抛的次数 n n n 是已知的。
假设一枚硬币质地均匀,也就是说抛一次硬币,出现正面向上和反面向上的概率 p p p 都为0.5,然后抛10次,下图是正面向上出现0次到10次的概率图:

附绘图代码
import numpy as np import matplotlib.pyplot as plt from scipy.stats import binom #plt.rcParams['font.family']=['Arial Unicode MS'] n = 10 #试验次数 p = 0.5 #正面向上的概率 #生成x轴的数据点 x = np.arange(0, n + 1, 0.001) #二项分布的概率质量函数(PMF)和累积分布函数(CDF) pmf = binom.pmf(x, n, p) #cdf = binom.cdf(x, n, p) plt.figure(figsize=(10, 5)) plt.subplot(121) plt.plot(x, pmf, 'b-', lw=2, label='PMF') plt.vlines(x, 0, pmf, colors='b', lw=1, alpha=0.5) plt.xlabel('正面向上次数') plt.ylabel('概率') plt.title('二项分布-抛硬币10次') plt.legend() plt.show()
正常来说,我们可以提前就预料到结果中出现5次正面向上的概率最大,实际上也雀食如此。但这是对质地均匀的硬币来说的,如果是一枚质地不均匀的硬币,我们还能这么信誓旦旦地判断吗?
再假设我们拿到了一枚不知道是否质地均匀的硬币,然后想求抛一次硬币正面向上的概率。这个问题如何解决呢?
一个粗糙的解决方案是: 我尽可能地多抛硬币,然后看所有结果中正面向上出现的概率是多少,这个概率就是抛一次硬币正面向上的概率的逼近。比如我茶不思饭不想地连续抛了10000次硬币,其中出现正面向上的有3000次,现在我可以自信地说再抛一次硬币正面向上的概率 大概 就是0.3。注意我这里用了大概两个字,也就是说0.3这个概率只是抛一次硬币中正面向上出现的所有概率中最大的一个概率,那有没有可能是0.4、0.5甚至0.9呢?是有可能的,只是这些概率出现的概率都相对0.3 更低 罢了。
再试想一下,我只抛了100次,其中出现正面向上的有30次,那我判断再抛一次硬币正面向上的概率是0.3的 把握 是不是会比10000次出现3000次 更低 呢?
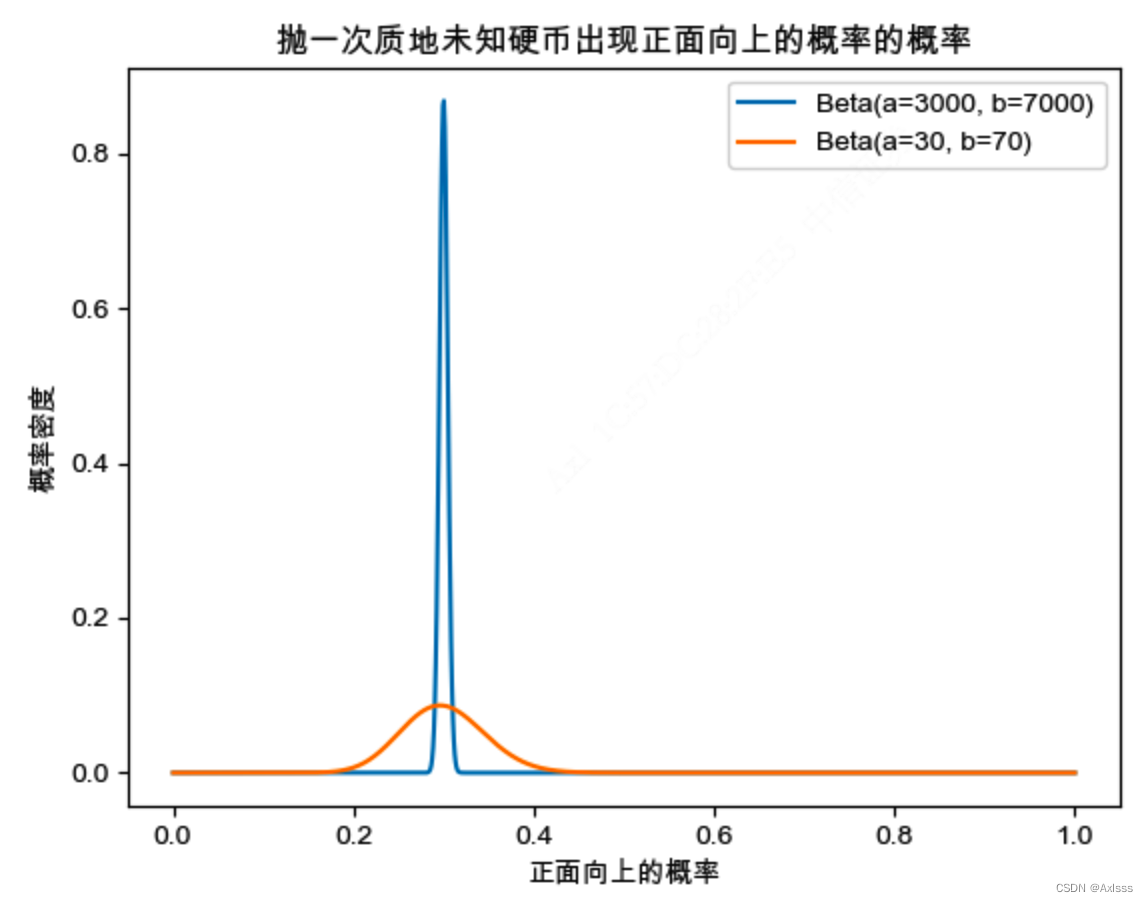
用图展示一下抛一次质地未知硬币出现正面向上的概率的概率(先验知识是已知抛了n次中出现正面向上的有a次):
附绘图代码
import numpy as np import matplotlib.pyplot as plt from scipy.stats import beta #plt.rcParams['font.family']=['Arial Unicode MS'] a1 = 3000 # 抛一万次硬币中正面向上的次数 b1 = 7000 # 抛一万次硬币中反面向上的次数 a2 = 30 # 抛一百次硬币中正面向上的次数 b2 = 70 # 抛一百次硬币中反面向上的次数 x = np.linspace(0.0, 1.0, 1000) # 计算Beta分布的概率密度函数值 y1 = beta.pdf(x, a1, b1) y2 = beta.pdf(x, a2, b2) plt.plot(x, y1, label='Beta(a={}, b={})'.format(a1, b1)) plt.plot(x, y2, label='Beta(a={}, b={})'.format(a2, b2)) plt.xlabel('正面向上的概率') plt.ylabel('概率密度') plt.title('抛一次质地未知硬币出现正面向上的概率的概率') plt.legend() plt.show()
这个图像表示了抛一次质地未知硬币出现正面向上的概率的概率分布,其中图像的形状随参数a和b的不同而变化。从图中可以看出:
- 基于抛10000次硬币中出现正面向上3000次的是蓝色曲线,其在横坐标上正面向上的概率为0.3处取得最大值,即再抛一次硬币出现正面向上的概率是0.3的结果最为确信;
- 基于抛100次硬币中出现正面向上30次的是橙色曲线,其也在横坐标上正面向上的概率为0.3处取得最大值,即再抛一次硬币出现正面向上的概率是0.3的结果最为确信,但与蓝色曲线对比可以看出,明显橙色曲线对此判断的把握要比蓝色曲线小得多;
那么如何去量化上面提到的 更低 与 把握 ?此时就该Beta分布登场了!
细心的小伙伴可以看出上图就是用Beta函数画出来的图像。
文章开头说过Beta分布的表示为 X X X~ B e t a ( a , b ) Beta(a,b) Beta(a,b) ,其中 a 、 b a、b a、b 是形状参数,可以控制图像的形状。对应到抛硬币场景中,