本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-自动控制原理Ch1-6根轨迹Root locus
- 1. 根的作用
- 2. 手绘技巧
- 3. 分离点/汇合点&根轨迹的几何性质
1. 根的作用
G
(
s
)
=
s
+
3
s
2
+
2
s
+
4
G\left( s \right) =\frac{s+3}{s^2+2s+4}
G(s)=s2+2s+4s+3
Matlab可绘制 riocus(g)
掌握根的变化规律 , 设计控制器,补偿器 : Compentator Lead Lag…
根 —— 极点
- 一阶系统

- 二阶系统


- 三阶系统


2. 手绘技巧
Matlab可以精确绘制——手绘——掌握根的变化规律——设计控制器
根轨迹的基本形式
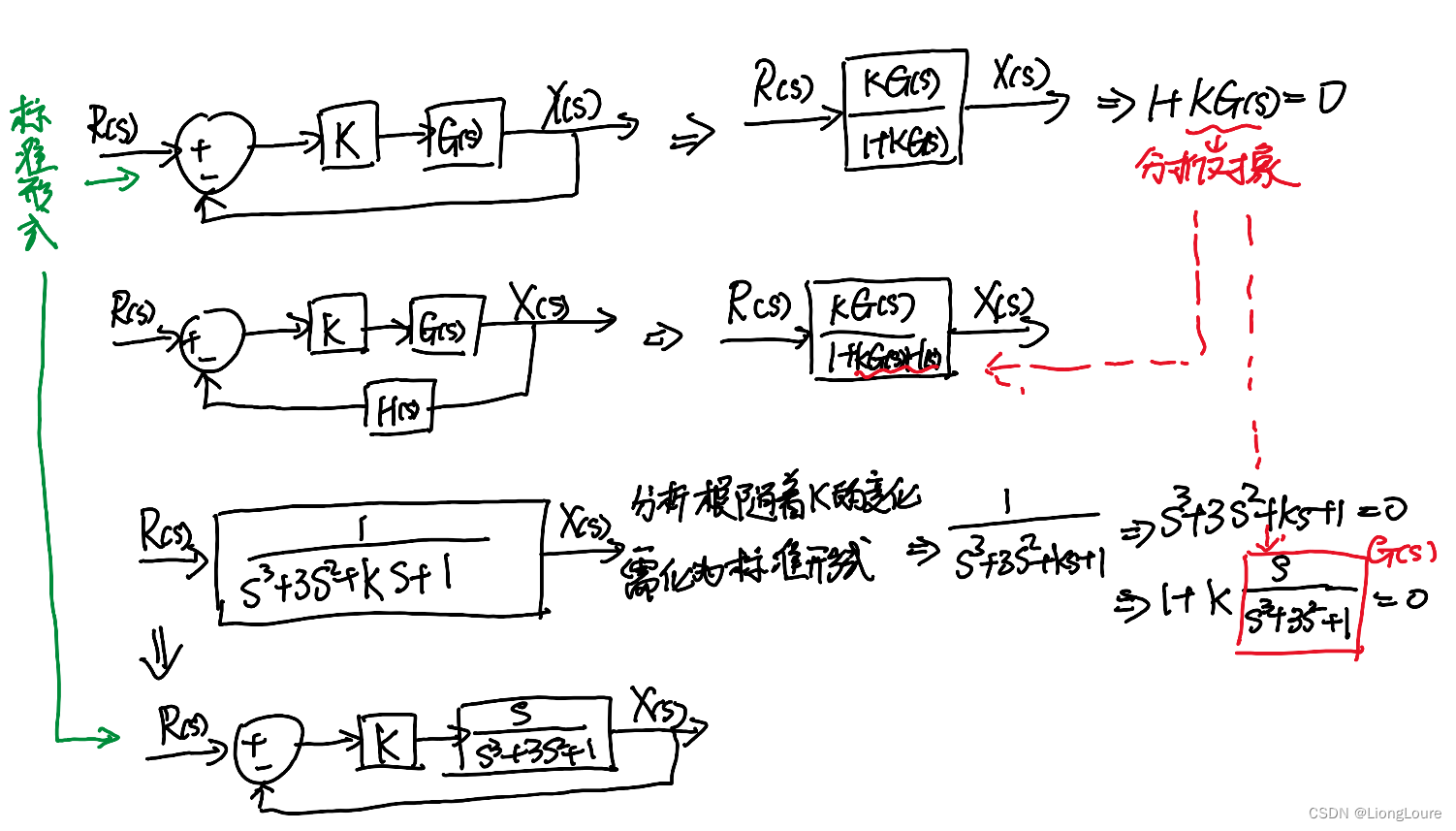
根轨迹研究的是: 当
K
K
K从0到
+
∞
+\infty
+∞时,闭环系统根(极点)位置的变化规律
1 + K G ( s ) = 0 , G ( s ) = N ( s ) D ( s ) = ( s − z 1 ) ( s − z 2 ) ⋯ ( s − z m ) ( s − p 1 ) ( s − p 2 ) ⋯ ( s − p n ) 1+KG\left( s \right) =0,G\left( s \right) =\frac{N\left( s \right)}{D\left( s \right)}=\frac{\left( s-z_1 \right) \left( s-z_2 \right) \cdots \left( s-z_{\mathrm{m}} \right)}{\left( s-p_1 \right) \left( s-p_2 \right) \cdots \left( s-p_{\mathrm{n}} \right)} 1+KG(s)=0,G(s)=D(s)N(s)=(s−p1)(s−p2)⋯(s−pn)(s−z1)(s−z2)⋯(s−zm)
其中,
z
1
⋯
z
m
z_1\cdots z_{\mathrm{m}}
z1⋯zm 为零点 Zeros
⊙
\odot
⊙ ,
p
1
⋯
p
n
p_1\cdots p_{\mathrm{n}}
p1⋯pn 为极点 Poles
×
\times
×
规则1 :共有
n
n
n条根轨迹, 若
n
>
m
n>m
n>m;共有
m
m
m条根轨迹,若
m
>
n
m>n
m>n;
⇐
max
{
m
,
n
}
\Leftarrow \max \left\{ m,n \right\}
⇐max{m,n}
规则2 :若
m
=
n
m=n
m=n,随着
K
K
K从
0
→
∞
0\rightarrow \infty
0→∞ , 根轨迹从
G
(
s
)
G\left( s \right)
G(s)的极点向零点移动:
1
+
K
G
(
s
)
=
0
⇒
D
(
s
)
+
K
N
(
s
)
=
0
1+KG\left( s \right) =0\Rightarrow D\left( s \right) +KN\left( s \right) =0
1+KG(s)=0⇒D(s)+KN(s)=0 ,
K
→
0
K\rightarrow 0
K→0 时
D
(
s
)
=
0
D\left( s \right) =0
D(s)=0(极点);
K
→
∞
K\rightarrow \infty
K→∞ 时
N
(
s
)
=
0
N\left( s \right) =0
N(s)=0 (零点)
规则3:实轴上的根轨迹存在于从右向左第奇数个极点/零点的左边
规则4:若附属跟存在,则一定是共轭的,所以根轨迹通过实轴对称
规则5:若
n
>
m
n>m
n>m , 则有
n
−
m
n-m
n−m个极点指向无穷;若
m
>
n
m>n
m>n , 则有
m
−
n
m-n
m−n条根轨迹从无穷指向零点
规则6:根轨迹延渐近线移动,渐近线与实轴的交点
σ
=
∑
p
−
∑
z
n
−
m
\sigma =\frac{\sum{p}-\sum{z}}{n-m}
σ=n−m∑p−∑z ,渐近线与实轴的夹角
θ
=
2
q
+
1
n
−
m
π
,
q
=
0
,
1
,
.
.
.
,
n
−
m
−
1
/
m
−
n
−
1
\theta =\frac{2q+1}{n-m}\pi ,q=0,1,...,n-m-1/m-n-1
θ=n−m2q+1π,q=0,1,...,n−m−1/m−n−1

3. 分离点/汇合点&根轨迹的几何性质
以 2nd-order system 为例:

Properties of Root locus