旋转矩形问题

news2024/11/26 8:24:50

问题：判断两个旋转矩形是否重叠（相交和包含）

矩形的坐标是旋转前的坐标：
矩形A(left1,top1,width1,height1,angle1)
矩形B(left2,top2,width2,height2,angle2)

方法1：碰撞检测判断相交 + 点在多边形内部判断包含

遍历A的所有边，并与B的所有边做相交判断。该方法适用于所有的多边形相交碰撞检测问题

相交的定义为：重叠部分的面积>0，故相切情况不属于相交

不属于相交情况下，再判断包含的情况：
取矩阵A中心点P，判断P是否在矩阵B内部，同理判断矩阵B中心点P’是否在矩阵A内部，
两次判断只要有一次属于内部即可判断处于包含情况。

1.判断两线段相交

  • 快速排斥
    一个线段中 x 较大的端点是否小于另一个线段中 x 较小的段点，若是，则说明两个线段必然没有交点，同理判断下 y
  • 跨立实验
    判断 A 点与 B 点是否在线段 DC 的两侧，即向量 DA 与向量 DB 分别在向量 DC 的两端，也就是其两个叉积结果是异号的,即
    (DA 叉乘 DC) * (DB 叉乘 DC) < 0
    同时还需要证明 C 点与 D 点在线段 AB 的两端，两个同时满足，则表示线段相交

注意： 共线情况可以通过跨立实验，不过在快速排斥阶段就被剔除了

// 判断线段AB 和线段CD 是否相交
function judgeSegmentsIntersect (A, B, C, D) {
  //快速排斥, 不考虑相切情况 判断时要算上等于
  if (Math.max(C.x, D.x) <= Math.min(A.x, B.x) || Math.max(C.y, D.y) <= Math.min(A.y, B.y) ||
    Math.max(A.x, B.x) <= Math.min(C.x, D.x) || Math.max(A.y, B.y) <= Math.min(C.y, D.y)) {
    return false
  }
  // 向量叉乘
  const crossMul = (v1, v2) => {
    return v1.x * v2.y - v1.y * v2.x
  }
  const vector = (start, end) => {
    return {
      x: end.x - start.x,
      y: end.y - start.y
    }
  }
  let AC = vector(A, C)
  let AD = vector(A, D)
  let BC = vector(B, C)
  let BD = vector(B, D)
  let CA = vector(C, A)
  let DA = vector(D, A)
  let CB = vector(C, B)
  let DB = vector(D, B)
  return (crossMul(AC, AD) * crossMul(BC, BD) <= 0)
    && (crossMul(CA, CB) * crossMul(DA, DB) <= 0)
}

2. 判断矩形相交

// 绕原点逆时针旋转后的点坐标
// 默认绕原点旋转
const rotate = ({ x, y }, deg, origin = { x: 0, y: 0 }) => ({
  x: (x - origin.x) * Math.cos(deg) + (y - origin.y) * Math.sin(deg) + origin.x,
  y: (origin.x - x) * Math.sin(deg) + (y - origin.y) * Math.cos(deg) + origin.y
})
const toDeg = (angle) => angle / 180 * Math.PI
const getCenterPoint = (box) => ({
  x: box.left + box.width / 2,
  y: box.top + box.height / 2
})
/**
 * 转化为顶点坐标数组
 * @param {Object} box 
 */
function toRect (box) {
  let deg = toDeg(box.angle)
  let cp = getCenterPoint(box)
  return [rotate({
    x: box.left,
    y: box.top
  }, deg, cp), rotate({
    x: box.left + box.width,
    y: box.top,
  }, deg, cp), rotate({
    x: box.left + box.width,
    y: box.top + box.height,
  }, deg, cp), rotate({
    x: box.left,
    y: box.top + box.height
  }, deg, cp)]
}
/**
 * 判断矩形相交
 */
function judgeRectanglesIntersect (box1, box2) {
  let rect1 = toRect(box1)
  let rect2 = toRect(box2)
  for (let i = 0; i < rect1.length; i++) {
    let A = rect1[i]
    let B = i === rect1.length - 1 ? rect1[0] : rect1[i + 1]
    for (let j = 0; j < rect2.length; j++) {
      let C = rect2[j]
      let D = j === rect2.length - 1 ? rect2[0] : rect2[j + 1]
      if (judgeSegmentsIntersect(A, B, C, D)) {
        return true
      }
    }
  }
  return false
}

3. 判断矩阵包含

/**
 * 已知两矩形不相交
 * 判断矩形是否属于包含关系
 * @param {*} rect1 
 * @param {*} rect2 
 */
function judgeRectanglesContain (box1, box2) {
  const getCenterPoint = (box) => ({
    x: box.left + box.width / 2,
    y: box.top + box.height / 2
  })
  let p1 = getCenterPoint(box1)
  let p2 = getCenterPoint(box2)
  // 点P需要绕另一个点P'逆时针旋转得到新的位置
  let np1 = rotate(p1, toDeg(box2.angle), p2)
  let np2 = rotate(p2, toDeg(box1.angle), p1)
  // 判断点P是否在水平坐标系的矩形box中
  const isInside = (p, { left, top, width, height }) => {
    return p.x >= left && p.x <= left + width && p.y >= top && p.y <= top + height
  }
  return isInside(np1, box2) || isInside(np2, box1)
}

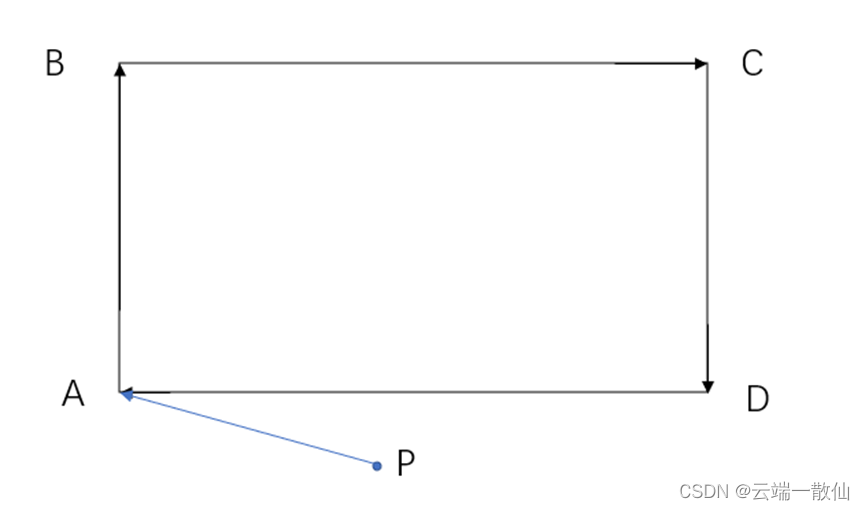
在这里插入图片描述
求出相交的点：
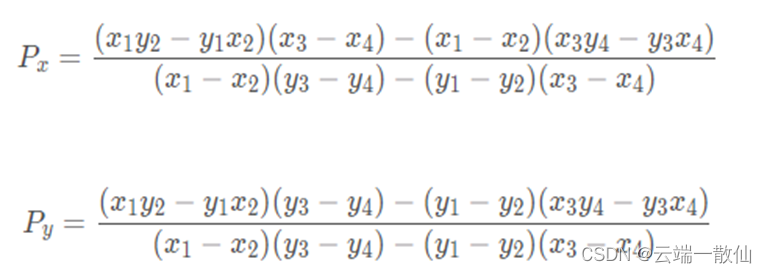
在这里插入图片描述

4.计算相交区域面积

计算所有顶点的横纵坐标均值，记作中心点，计算中心点到每个点的单位向量，以x轴正方向为起始边，按照顺时针方向扫描360度，对扫描到的点进行排序，先考虑从180度到360度，y>0，x从-1到1递增，对于从0到180度，y<0，x从1到-1递减。然后计算三角形面积(利用叉积) 最后将三角形面积求和。

方法2：分离轴定律/OBB方向包围盒算法

参考文章 矩形旋转碰撞,OBB方向包围盒算法实现

简单说 包围盒 就是用一个方便分离轴的规则形状去包围一个物体
而 分离轴定律 即是根据两个多边形在所有轴上的投影是否重叠判断是否碰撞

如何检测轴投影是否重叠？有两种方法。

  1. 计算每个矩形在检测轴的最大投影坐标区间，判断两个坐标区间是否重叠
  2. 计算每个矩形的半径投影（该矩形在检测轴的投影大小的一半），将这两个投影长度之和与两个矩形中心点连线在检测轴上投影的长度比较
    这里我们采用第二种。
    首先确定检测轴向量，为了计算方便，我们假设 检测轴向量 为单位向量,取值(cosθ,sinθ),其中 θ 为该向量与x轴的夹角，大小始终>0,对于另一坐标轴为90-θ
    然后计算半径投影
    检测轴为自身的矩形，半径投影即该检测轴长度的一半
    检测轴在另一个矩形，半径投影即该矩形两边长在检测轴上投影大小之和的一半
    假设目标轴为向量A,检测轴为向量B,则目标轴在检测轴上的投影为
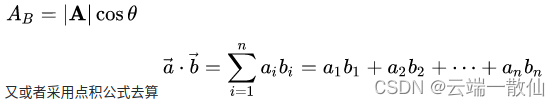
    在这里插入图片描述
    上面提到 检测轴向量 为单位向量，所以目标轴向量（x,y）在检测轴上的投影为 x·cosθ+y·sinθ，即
/**
 * 计算投影半径
 * @param {Array(Number)} checkAxis 检测轴 [cosθ,sinθ]
 * @param {Array} axis 目标轴 [x,y]
 */
function getProjectionRadius (checkAxis, axis) {
  return Math.abs(axis[0] * checkAxis[0] + axis[1] * checkAxis[1])
}

全部代码如下：

// 绕原点逆时针旋转后的点坐标
// 默认绕原点旋转
const rotate = ({ x, y }, deg, origin = { x: 0, y: 0 }) => ({
  x: (x - origin.x) * Math.cos(deg) + (y - origin.y) * Math.sin(deg) + origin.x,
  y: (origin.x - x) * Math.sin(deg) + (y - origin.y) * Math.cos(deg) + origin.y
})
const toDeg = (angle) => angle / 180 * Math.PI
const getCenterPoint = (box) => ({
  x: box.left + box.width / 2,
  y: box.top + box.height / 2
})
/**
 * 转化为顶点坐标数组
 * @param {Object} box 
 */
function toRect (box) {
  let deg = toDeg(box.angle)
  let cp = getCenterPoint(box)
  return [rotate({
    x: box.left,
    y: box.top
  }, deg, cp), rotate({
    x: box.left + box.width,
    y: box.top,
  }, deg, cp), rotate({
    x: box.left + box.width,
    y: box.top + box.height,
  }, deg, cp), rotate({
    x: box.left,
    y: box.top + box.height
  }, deg, cp)]
}
/**
 * 计算投影半径
 * @param {Array(Number)} checkAxis 检测轴 [cosθ,sinθ]
 * @param {Array} axis 目标轴 [x,y]
 */
function getProjectionRadius (checkAxis, axis) {
  return Math.abs(axis[0] * checkAxis[0] + axis[1] * checkAxis[1])
}
/**
 * 判断是否碰撞
 * @param {Array} rect1 矩形顶点坐标数组 [Pa,Pb,Pc,Pd]
 * @param {*} rect2 
 */
function isCollision (box1, box2) {
  let rect1 = toRect(box1)
  let rect2 = toRect(box2)
  const vector = (start, end) => {
    return [end.x - start.x, end.y - start.y]
  }
  // 两个矩形的中心点
  const p1 = getCenterPoint(box1)
  const p2 = getCenterPoint(box2)
  //向量 p1p2
  const vp1p2 = vector(p1, p2)
  //矩形1的两边向量
  let AB = vector(rect1[0], rect1[1])
  let BC = vector(rect1[1], rect1[2])
  //矩形2的两边向量
  let A1B1 = vector(rect2[0], rect2[1])
  let B1C1 = vector(rect2[1], rect2[2])
  // 矩形1 的两个弧度
  let deg11 = toDeg(box1.angle)
  let deg12 = toDeg(90 - box1.angle)
  // 矩形2 的两个弧度
  let deg21 = toDeg(box2.angle)
  let deg22 = toDeg(90 - box2.angle)
  // 投影重叠
  const isCover = (checkAxisRadius, deg, targetAxis1, targetAxis2) => {
    let checkAxis = [Math.cos(deg), Math.sin(deg)]
    let targetAxisRadius = (getProjectionRadius(checkAxis, targetAxis1) + getProjectionRadius(checkAxis, targetAxis2)) / 2
    let centerPointRadius = getProjectionRadius(checkAxis, vp1p2)
    console.log(`checkAxis:${checkAxis},三个投影:${checkAxisRadius}, ${targetAxisRadius}, ${centerPointRadius}`)
    return checkAxisRadius + targetAxisRadius > centerPointRadius
  }
  return isCover(box1.width / 2, deg11, A1B1, B1C1) &&
    isCover(box1.height / 2, deg12, A1B1, B1C1) &&
    isCover(box2.width / 2, deg21, AB, BC) &&
    isCover(box2.height / 2, deg22, AB, BC)
}
(function main () {
  let box1 = {
    left: 0,
    top: 0,
    width: 100,
    height: 100,
    angle: 30
  }
  let box2 = {
    left: 100,
    top: 0,
    width: 100,
    height: 100,
    angle: 0
  }
  return isCollision(box1, box2)
})()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1342866.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

单片机开发从小工到专家

单片机开发从小工到专家

有道无术&#xff0c;术尚可求&#xff1b;有术无道&#xff0c;止于术 背景 向单片机嵌入式开发小伙伴推荐了几本书&#xff0c;阅读量破10 1. 适用范围 2. 书籍推荐 书籍推荐 3. 大师介绍 大师介绍 4. 大师书籍编写逻辑 25年大师出版的关于&#xff1a;嵌入式单片…
阅读更多...
JAVA中的回调函数

JAVA中的回调函数

回调函数的基本概念&#xff1a; 回调函数是一种常见的编程模式&#xff0c;也称为回调机制。回调函数是一种特殊的函数&#xff0c;它允许将一段代码作为参数传递给另一个方法&#xff0c;并在需要时调用。回调函数通常用于异步编程或事件处理&#xff0c;可以将程序的控制权…
阅读更多...
NFC物联网智能购物车设计方案

NFC物联网智能购物车设计方案

智能购物车是综合利用计算机网络、射频识别技术、数据库技术、单片机于一体的设备具有先进性、便于管理性、经济性、普适性。基于NFC (Near Field Communication&#xff0c;近场通信)技术的智能购物车&#xff0c;能够大幅缩短结账排队时间&#xff0c;实现“无感支付”。NFC是…
阅读更多...
对SPI总线上挂接多个X5045的读写操作

对SPI总线上挂接多个X5045的读写操作

#include<reg51.h> //包含单片机寄存器的头文件 #include<intrins.h> //包含_nop_()函数定义的头文件 sbit SCKP3^4; //将SCK位定义为P3.4引脚 sbit SIP3^5; //将SI位定义为P3.5引脚 sbit SOP3^6; //将SO位定义为P3.6引脚 sbit CS1P3^7; …
阅读更多...
【js控制页面的模糊程度】【lenis禁止页面滚动】

【js控制页面的模糊程度】【lenis禁止页面滚动】

文章目录 前言一、效果图二、使用步骤1.下载studio-freight/lenis2.使用studio-freight/lenis 三、下载 gsap在编写页面动画1. 下载gsap2.引入gsap3.调用gsap的方法&#xff0c;让页面模糊 总结 前言 在项目中&#xff0c;我们经常会遇到弹窗功能&#xff0c;当弹框弹出时&…
阅读更多...
MPI并行程序设计 —— C 和 fortran 环境搭建 openmpi 示例程序

MPI并行程序设计 —— C 和 fortran 环境搭建 openmpi 示例程序

1.安装环境 wget https://download.open-mpi.org/release/open-mpi/v4.1/openmpi-4.1.6.tar.g tar zxf openmpi-4.1.6.tar.gz cd openmpi-4.1.6/ 其中 configure 选项 --prefix/.../ 需要使用绝对路径&#xff0c;例如&#xff1a; ./configure --prefix/home/hipper/ex_open…
阅读更多...
python subprocess run 和 Popen 的一些使用和注意事项

python subprocess run 和 Popen 的一些使用和注意事项

文章目录 一、run二、Popen NAME subprocess - Subprocesses with accessible I/O streams MODULE REFERENCE https://docs.python.org/3.9/library/subprocess The following documentation is automatically generated from the Python source files. It may be incomplete, …
阅读更多...
【事故总结】Mybatis-Wrapper导致的生产事故

【事故总结】Mybatis-Wrapper导致的生产事故

近期遭遇了一次生产环境的严重告警&#xff0c;涉及慢接口和CPU过载。经过排查&#xff0c;发现问题根源在于一段使用MyBatis的查询代码。当传入空列表作为查询条件时&#xff0c;MyBatis会忽略该条件&#xff0c;导致全表扫描&#xff0c;进而引发系统资源耗尽和频繁的Full GC…
阅读更多...
浅谈技术架构的演进过程

浅谈技术架构的演进过程

前言 最近在学习Redis、Doctor相关技术知识&#xff0c;它们与分布式系统有着很大的关系。 而对于分布式系统&#xff0c;它本身就是随着业务的不断推进&#xff0c;技术架构不断演进而得到发展和实现的。而所谓的分布式系统&#xff0c;实际上就是想办法引入更多的硬件资源&am…
阅读更多...
OpenHarmony之分布式软总线

OpenHarmony之分布式软总线

分布式软总线是多设备终端的统一基座&#xff0c;为设备间的无缝互联提供了统一的分布式通信能力&#xff0c;能够快速发现并连接设备&#xff0c;高效地传输任务和数据。 分布式软总线实现近场设备间统一的分布式通信管理能力&#xff0c;提供不区分链路的设备间发现连接、组网…
阅读更多...
消息队列基础知识

消息队列基础知识

学一点&#xff0c;整一点&#xff0c;基本都是综合别人的&#xff0c;弄成我能理解的内容 https://blog.csdn.net/BenJamin_Blue/article/details/125946812 https://blog.csdn.net/qq_46119575/article/details/129794304 &#x1f4cc;导航小助手&#x1f4cc; 生产者-消费者…
阅读更多...
14.12-常见的对于非阻塞复制的误解

14.12-常见的对于非阻塞复制的误解

常见的对于非阻塞复制的误解 1&#xff0c;非阻塞赋值和$display1.1&#xff0c;RTL案例1.2&#xff0c;功能实现1.3&#xff0c;解释误解 2&#xff0c;#0延时赋值2.1&#xff0c;RTL案例2.2&#xff0c;功能实现2.3&#xff0c;解释误解 3&#xff0c;对同一变量进行多次非阻…
阅读更多...
家用洗地机哪个牌子好？2024年洗地机热门品牌测评

家用洗地机哪个牌子好？2024年洗地机热门品牌测评

随着科技水平的不断发展&#xff0c;人们对家居设备的要求也在不断提高&#xff0c;追求省时省力的家务工具变得越来越受欢迎。家用洗地机的出现满足了这一需求&#xff0c;其洗拖吸一体的特点使其成为现代家庭的必备神器。 使用家用洗地机可以极大地提高地面清洁的效率&#…
阅读更多...
因数据侵权，纽约时报起诉OpenAI、微软

因数据侵权，纽约时报起诉OpenAI、微软

12月28日&#xff0c;金融时报消息&#xff0c;因为非法使用数百万篇新闻数据训练ChatGPT等生成式AI产品&#xff0c;《纽约时报》正在起诉OpenAI和微软。 这是第一家起诉生成式AI厂商的著名媒体。《纽约时报》没有公布具体数额&#xff0c;但希望获得数十亿美元的赔偿金。 O…
阅读更多...
两向量叉乘值为对应平行四边形面积--公式推导

两向量叉乘值为对应平行四边形面积--公式推导

两向量叉乘值为对应平行四边形面积--公式推导 介绍 介绍
阅读更多...
PowerShell Instal 一键部署gitea

PowerShell Instal 一键部署gitea

gitea 前言 Gitea 是一个轻量级的 DevOps 平台软件。从开发计划到产品成型的整个软件生命周期，他都能够高效而轻松的帮助团队和开发者。包括 Git 托管、代码审查、团队协作、软件包注册和 CI/CD。它与 GitHub、Bitbucket 和 GitLab 等比较类似。 Gitea 最初是从 Gogs 分支而来…
阅读更多...
Ubuntu22.04-安装后Terminal无法调出

Ubuntu22.04-安装后Terminal无法调出

参考&#xff1a; Ubuntu20.04 终端打开不了的问题排查_ubuntu终端打不开-CSDN博客 https://blog.csdn.net/u010092716/article/details/130968032 Ubuntu修改locale从而修改语言环境_ubuntu locale-CSDN博客 https://blog.csdn.net/aa1209551258/article/details/81745394 问…
阅读更多...
2023年度总结：技术旅程的杨帆远航⛵

2023年度总结：技术旅程的杨帆远航⛵

文章目录 职业规划与心灵成长 ❤️‍&#x1f525;我的最大收获与成长 &#x1f4aa;新年Flag &#x1f6a9;我的技术发展规划 ⌛对技术行业的深度思考 &#x1f914;祝愿 &#x1f307; 2023 年对我来说是一个充实而令人难以忘怀的一年。这一年&#xff0c;我在CSDN上发表了 1…
阅读更多...
有效解决vcruntime140_1.dll丢失的问题，关于vcruntime140_1.dll文件

有效解决vcruntime140_1.dll丢失的问题，关于vcruntime140_1.dll文件

今天在使用电脑的过程中突然提示找不到vcruntime140_1.dll&#xff0c;出现这样的提示后&#xff0c;想要在打开程序时&#xff0c;有再一次提示找不到vcruntime140_1.dll&#xff0c;不能在正常打开程序&#xff0c;那么有什么办法可以解决vcruntime140_1.dll丢失的问题呢&…
阅读更多...
用python画最简单的图案,用python画小猫简单代码

用python画最简单的图案,用python画小猫简单代码

本篇文章给大家谈谈用python画小猫简单100行代码&#xff0c;以及用python画最简单的图案&#xff0c;希望对各位有所帮助&#xff0c;不要忘了收藏本站喔。 Source code download: 本文相关源码 from turtle import * #两个函数用于画心 defcurvemove():for i in range(200): …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023