原理

椭圆的扫描转换与圆的扫描转换有相似之处，但也有不同，主要区别是椭圆弧上存在改变主位移方向的临界点。瞬时针绘制四分椭圆弧的中点算法，根据对称性可以绘制完整的椭圆。

四分椭圆弧

中心在原点，长半轴为 $a$、短半轴为 $b$ 的椭圆隐函数方程为

$$F(x,y)=b^2{x}^2+a^2{y}^2-a^2{b}^2=0$$

四分法画椭圆算法：已知第一象限内的一点 $(x,y)$, 可以顺时针确定另外 3 个对称点 $(x,-y)$、$(-x,-y)$ 和 $(-x,y)$

临界分析

在临界点处，曲线的斜率为 $-1$

$$N(x,y)=N_{x_i}+N_{y_j}=\frac{\partial F}{\partial x}i+\frac{\partial F}{\partial y}j=2b^2{x}_i+2a^2{y}_j$$

法矢量的 $x$ 方向的分量为 $N_x=2b^{2}x$, 法矢量的 $y$ 方向为 $Ny$ = 2a^2y.从曲线上一点的法矢量角度看，在区域 $\mathbf{I}$ 内，$N_x<N_y$ 在临界点处， $N_x=N_y$ 在区域 $Ⅱ$ 内，$N_x>N_y$。显然，在临界点处，法矢量分量的大小发生了变化。

从曲线上的斜率角度来看，在临界点处，斜率为 $-1$, 区域内 $Ⅰ$ 内， $dx>dy$, 所以 $x$ 方向为主位移方向，在临界点处，有 $dx=dy$, 在区域内 $Ⅱ$ 内，$dy>dx$， 所以 $y$ 方向为主位移方向。在临界点处，主位移方向发生了改变。

在区域 $Ⅰ$ ， $x$ 方向上每次递增一个单位，$y$ 方向上减 1 或 减 0， 取决于中点误差项的值，在区域 $Ⅱ$， $y$ 方向上每次递增一个单位，$x$ 方向上加 1 或 加 0 取决于中点误差项的值。

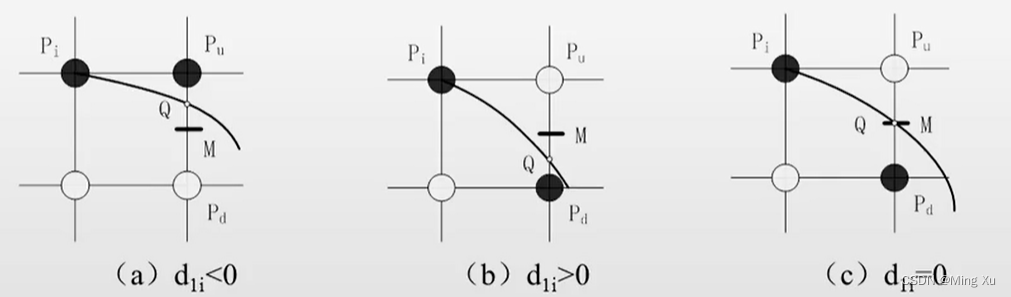
构造区域 $I$ 的中点误差项

从当前点 $P_i$ 出发选取一个像素点时，需将 $P_u$ 和 $P_d$ 两个候选像素连线的网格中点 $M$ $(x_i+1,y_i-0.5)$ 代入隐函数的方程，构造中点误差项 $d_{1i}$

$$d_{1i}=F(x_i+1,y_i-0.5)=b^2(x_i+1{)}^2+a^2(y_i-0.5{)}^2-a^2{b}^2$$

$$y_{i+1}=\{\begin{array}{ll}{y}_i& d_{1i}<0\\ yi-1& d_{1}i\ge 0\end{array}$$

中点误差项 $d_{1i}$ 的递推公式

$d_{1}i<0$ 区域内 $Ⅰ$ 内中点的递推

$$d_{1i+1}=d_{1i}+b^2(x_i+3)$$

$d_{1}i\ge 0$ 区域内 $Ⅰ$ 内中点的递推

$$d_{1i+1}=d_{1i}+b^2(x_i+3)+a^2(-2y_i+2)$$

中点误差项 $d_{1}i$ 的初值

在区域 $Ⅰ$ 内，椭圆弧的起点扫描转换后的像素点为 $P_0(a,b)$ 沿着主位移 $x$ 的方向递增一个单位，第一个参与判断的中点是 $M(1，b-0.5)$， 响应的中点误差项 $d_{1i}$

$$d_{10}=b^2+a^2(-b+0.25)$$

构造区域 $Ⅱ$ 的中点误差项

在区域 $Ⅱ$内，主位移方向发生变化，由 $x$ 方向转变为 $y$ 方向，从区域 $Ⅰ$ 椭圆弧的终点，$P_i(x_i,y_i)$ 出发选取下一像素时，需将 $P_1(x_i，y_i-1)$ 和 $P_r(x_I+1,y_i+1)$
的中点，$M(x_i+0.5,y_i-1)$ 代入隐函数方程，构造中点误差项 $d_{2i}$

$$d_{2i}=F(x_i+0.5,y_i-1)=b^2(x_i+0.5{)}^2+a^2(y_i-1{)}^2-a^2{b}^2$$

$$x_{i+1}=\{\begin{array}{ll}{x}_i+1& d_{2i}<0\\ xi& d_{2i}\ge 0\end{array}$$

中点误差项 $d_{2i}$ 的递推公式

$d_{2i}<0$ 区域 $Ⅰ$ 内中的递推
$$d_{2(i+1)}=d_{2i}+b^2(2x_i+2)+a^2(-2y_i+3)$$

$d_{2i}\ge 0$ 区域 $Ⅰ$ 内中的递推

$$d_{2(i+1)}=d_{2i}+a^2(-2y_i+3)$$

中点误差项 $d_{2i}$ 的初始值

假定 $P_i(x_i,y_i)$ 点为区域 $Ⅰ$ 内椭圆弧上的最后一个像素，$M_I(xi+1,y_{i-0.5})$ 是 $p_u$ 和 $p_d$ 像素的中点，满足 $x$ 方向分量小于 $y$ 方向分量

$$b^2(x_i+1)<a^2(y_i-0.5)$$

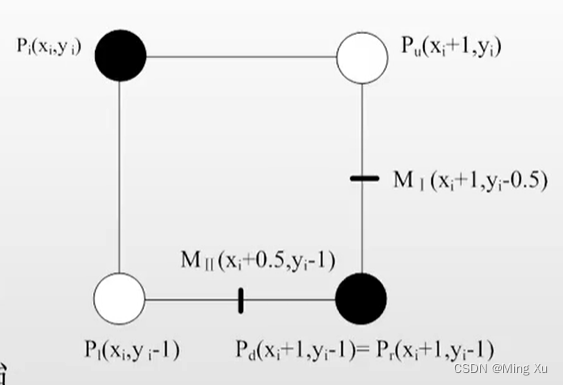
而在下一个中点处，不等号改变方向，则说明椭圆弧从区域 $Ⅰ$ 转入了区域 $Ⅱ$。 在区域 $Ⅱ$ 内，中点转换为 $M_{Ⅱ}(x_i+0.5,y_i-1)$, 用于判断选取 $P1$ 和 $P_r$ 像素，所以区域 $Ⅱ$ 内椭圆弧中电误差项 $d$ 的初始值为

$$d_{2,0}=b^2(x+0.5{)}^2+a^2(y-1{)}^2-a^2{b}^2$$

算法

1. 读入椭圆的长半轴 $a$ 和短半轴 $b$
2. 定义椭圆当前坐标 $x$， $y$ 定义中点误差项 $d_1$ 和 $d_2$ 定义像素颜色 cColoer
3. 计算 $d_{10}=b^2+a^2(-b+0.25)$， $x=0$, $y=0$，cColor=RGB(0, 0, 255)
4. 绘制点 $(x, y) $及其在四分椭圆中的另外 3个对称点
5. 判断 $d_1$ 的符号，若 $d_1<0$ 则 $(x,y)更新为$ $(xi+1,y)$, $d_1$ 更新为 $d_1+b^2(2x+3)$； 否则$(x,y)更新为$ $(xi+1,y-1)$, $d_1$ 更新为 $d_1+b^2(2x+3)+a^2(-2y+2)$；
6. 当 $b^2(x_i+1)<a^2(y_i-0.5)$ 时，重复 (4) 与 (5) 否则转到步骤 (7)
7. 计算下半部分 $d_2$ 的初值，$d_{20}=b^2(x+0.5{)}^2+a^2(y-1{)}^2-a^2{b}^2$
8. 绘制点 $(x,y)$ 及其在四分椭圆中的另外 3 个对称点
9. 判断 $d_2$ 的符号，若 $d_2<0$ 则 $(x,y)更新为$ $(xi+1,y-1)$ $d_2$ 更新为 $d_2+b_2^2(2x+2)+a^2(-2y+3)$ 否则$(x,y)更新为$ $(xi+1,y)$, $d_2$ 更新为 $d_2+a^2(2y+3)$
   10.如果 $y\ge 0$ 重复步骤 (8) 和 (9)

#include <QApplication>
#include <QPainter>
#include <QWidget>

void EllipsePoint(QPainter * painter, int x, int y) {
    QColor color(255, 0, 0);  // 设置为红色

    // 平移到正确的位置
    int centerX = 400;  // 窗口宽度的一半
    int centerY = 300;  // 窗口高度的一半

    painter->setPen(color);
    painter->drawPoint(centerX+x, centerY+y);
    painter->drawPoint(centerX+x, centerY-y);
    painter->drawPoint(centerX-x, centerY-y);
    painter->drawPoint(centerX-x, centerY+y);


}


void MidPointEllipse(QPainter* painter, int a, int b) {
    int x, y;
    x = 0, y = b;
    double d1 = b * b + a * a * (-b + 0.25);

    EllipsePoint(painter, x, y);

    while (b * b * (x+1) < a * a * (y-0.5)) {

        if (d1 < 0) {
            d1 += b * b * (2*x + 3);
        } else {
            d1 += b*b * (2*x + 3) + a* a*(-2*y +2);
            y--;
        }
        x++;
        EllipsePoint(painter, x, y);
    }
    double d2 = b * b * (x + 0.5) * (x + 0.5) + a * a * (y - 1) * (y -1) - a * a * b *b;
    while (y > 0) {
        if (d2 < 0) {
            d2 += b * b * (2*x + 2) + a * a * (-2*y + 3);
            x++;
        }else {
            d2 += a* a * (-2*y + 3);
        }
        y--;
        EllipsePoint(painter, x, y);
    }

}





class MyWidget : public QWidget {
public:
    MyWidget(QWidget* parent = nullptr) : QWidget(parent) {
        setFixedSize(800, 600);
    }

protected:
    void paintEvent(QPaintEvent* event) override {
        Q_UNUSED(event);

        QPainter painter(this);
        painter.setRenderHint(QPainter::Antialiasing, true);

//        int radius = 50;  // 圆的半径

        int a = 200;
        int b = 100;
//        MidPointCircle(&painter, radius);
        MidPointEllipse(&painter, a, b);

    }
};


int main(int argc, char* argv[]) {
    QApplication app(argc, argv);

    MyWidget widget;
    widget.show();

    return app.exec();
}