1、设置问题
投入的广告费越多,广告的点击量就越高,进而带来访问数的增加。
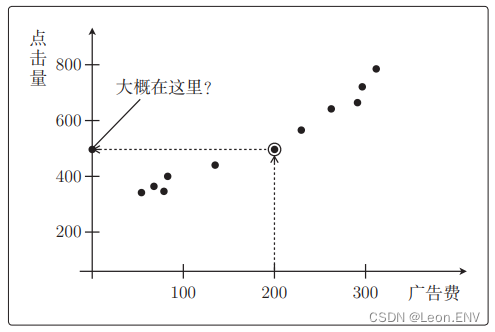
2、定义模型
定义一个函数:一次函数
y = ax + b (a 是斜率、b 是截距)
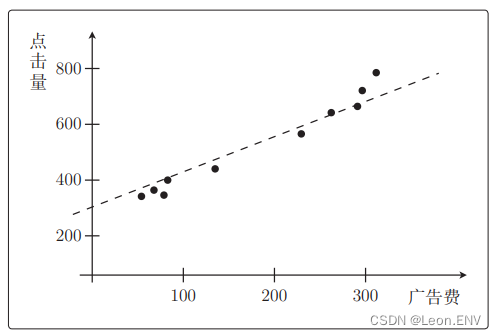
定义函数:
3、最小二乘法
例子:
用随便确定的参数计算的值与实际的值存在偏差。
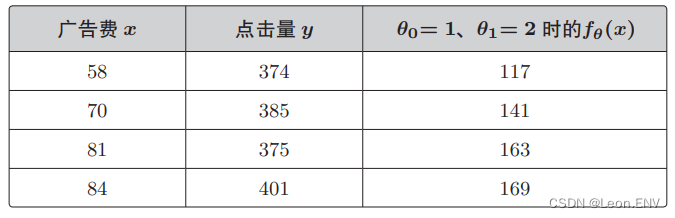

假设有 n 个训练数据, 那么它们的误差之和可以用这样的表达式表示。
这个表达式称为
目标函数,E(θ) 的 E 是误差的英语单词 Error 的首字母,∑读作“西格玛”。
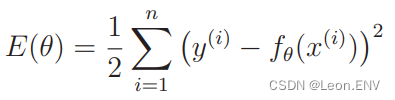
这么做是为了找到使 E(θ) 的值最小 的 θ,这样的问题称为最优化问题。
来计算一下表格 E(θ) 的值,设 θ0 = 1、θ1 = 2, 然后将刚才列举的 4 个训练数据代入表达式
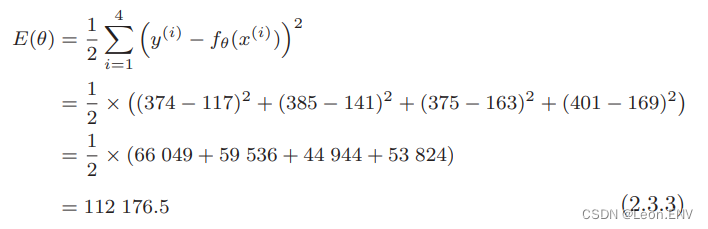
4、梯度下降法(最速下降法)
微分是计算变化的快慢程度时使用的方法。
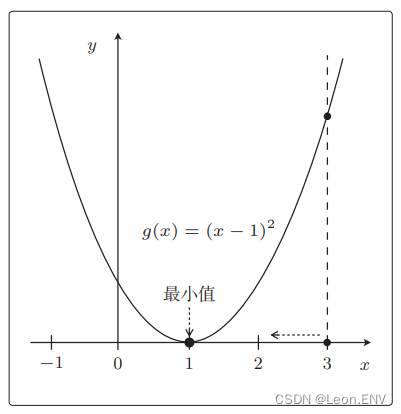
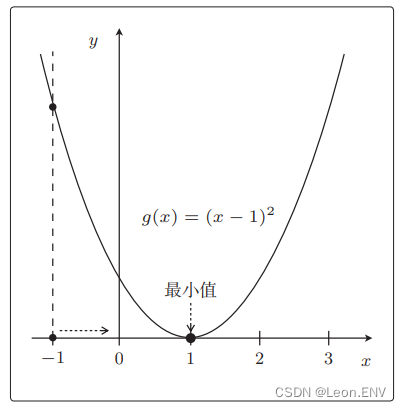
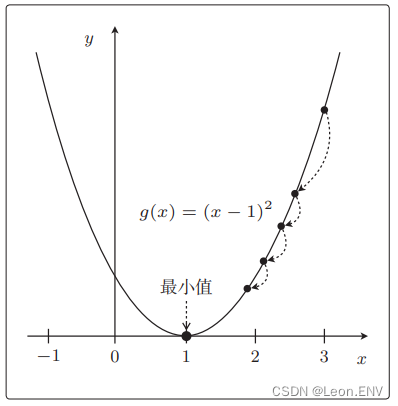
函数 g(x):
微分(求导):
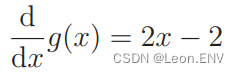
x < 1 为负数,x = 1 为0,x > 1 为正数。
根据导数的符号来决定移动 x 的方向,只要向与导数的符号相反的方向移动 x,g(x) 就会自然而然地沿着最小值的方向前进了, 这也被称为最速下降法或梯度下降法 。
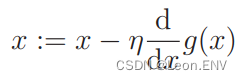
η 是称为学习率的正的常数,读作“伊塔”。根据学习率的大小, 到达最小值的更新次数也会发生变化。换种说法就是收敛速度会 不同。有时候甚至会出现完全无法收敛,一直发散的情况。
比如 η = 1,从 x = 3 开始 (结果是一直发散,无法收敛):
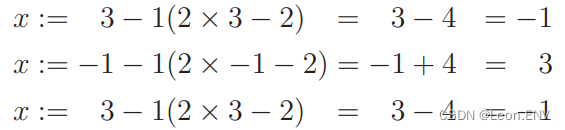
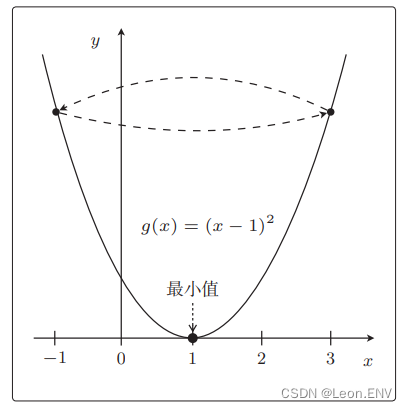
那设 η = 0.1,同样从 x = 3 开始:
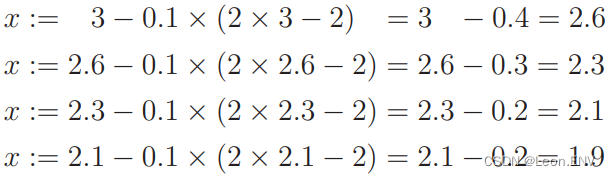
回过头来看一下目标函数 E(θ):
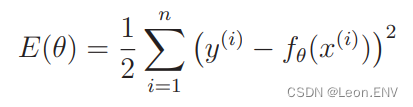
这个目标函数是拥有 θ0 和 θ1 的双变量函数,所以不能用 普通的微分,而要用偏微分:
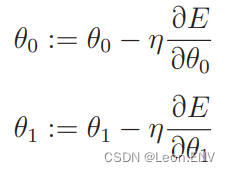
设:

计算微分:
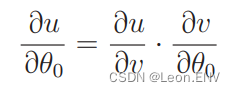
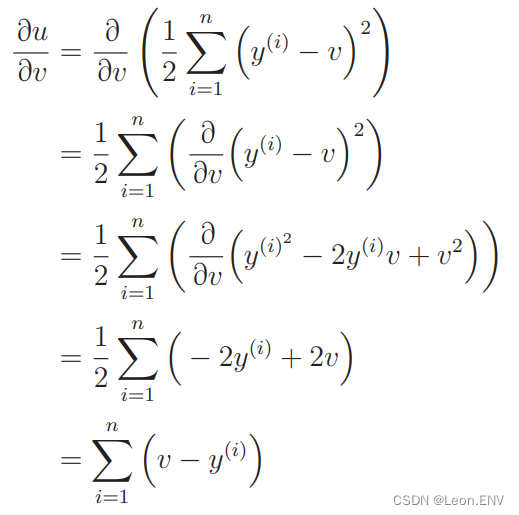
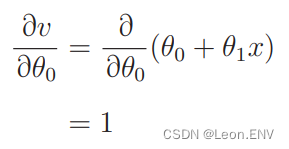

同样:
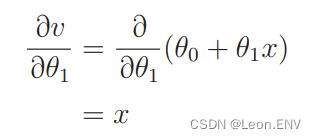
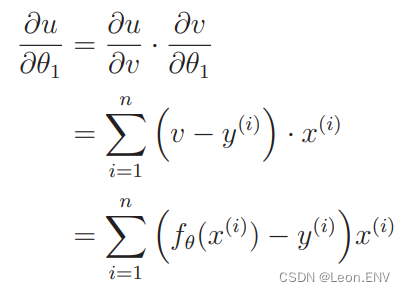
所以参数 θ0 和 θ1 的更新表达式是:

5、多项式回归
上面是一次函数,用更大次数的表达式, 这样就能表示更复杂的曲线。
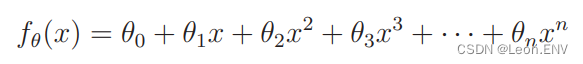
不过对于要解决的问题,在找出最合适的表达式之前,需要 不断地去尝试。
虽然次数越大拟合得越好,但难免也会出现过拟合的问题。
如二次函数:
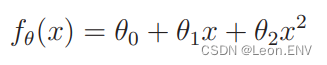
曲线如下:

曲线看起来更拟合数据。
计算微分:
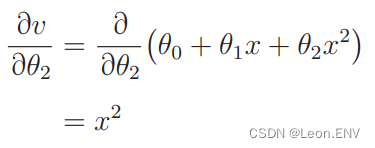
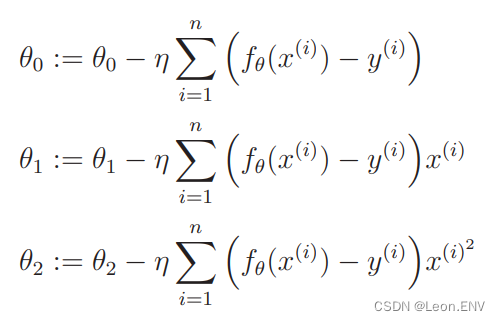
像这样增加函数中多项式的次数,然后再使用函数的分析方法被称为多项式回归。
6、多重回归
多项式回归问题中确实会涉及不同次数的项,但是使用的变量依然只有广告费一项。
我们稍微扩展一下之前设置的问题。之前只是根据广告费来预 测点击量,现在呢,决定点击量的除了广告费之外,还有广告的 展示位置和广告版面的大小等多个要素。
为了让问题尽可能地简单,这次我们只考虑广告版面的大小,设 广告费为 x1、广告栏的宽为 x2、广告栏的高为 x3,那么 fθ 可以 表示如下:
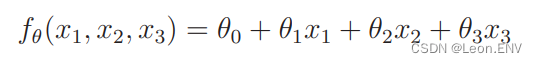
下面我们把它推广到有 n 个变量的情况:
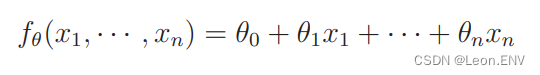
使用向量表示:
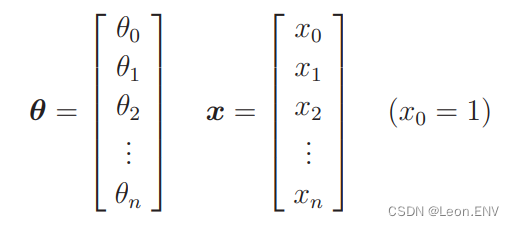
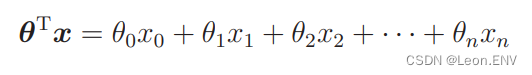
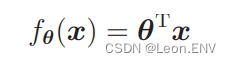
求微分:
u 对 v 微分的部分是一样的,所以只需要求 v 对 θj 的微分就好了
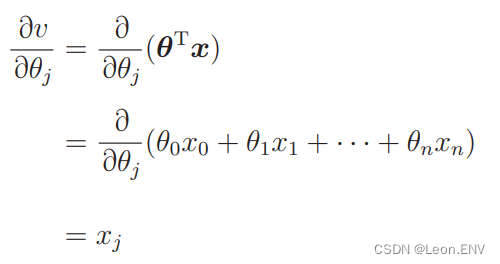
那么第 j 个参数的更新表达式就是这样的:
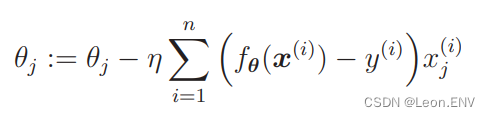
像这样包含了多个变量的回归称为多重回归。
7、随机梯度下降法
梯度下降法是对所有的训练数据都重复进行计算,缺点是计算量大、计算时间长,且容易陷入局部最优解 。
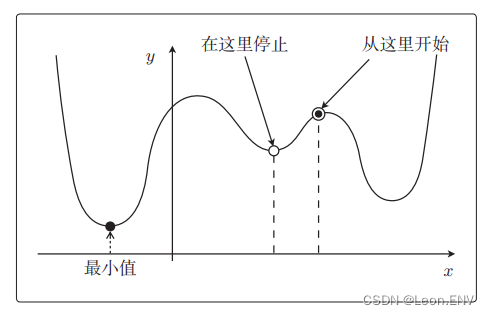
在随机梯度下降 法中会随机选择一个训练数据,并使用它来更新参数。这个表达 式中的 k 就是被随机选中的数据索引:
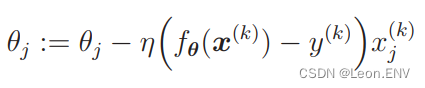
梯度下降法更新 1 次参数的时间,随机梯度下降法可以更新 n 次。 此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。
我们前面提到了随机选择 1 个训练数据的做法,此外还有随机选 择 m 个训练数据来更新参数的做法。
设随机选择 m 个训练数据的索引的集合为 K,那么我们这样 来更新参数:
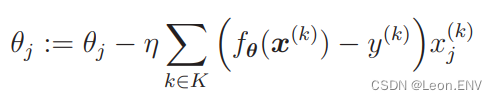
这种做法被称为小批量(mini-batch)梯度下降法。
不管是随机梯度下降法还是小批量梯度下降法,我们都必须考虑 学习率 η。
把 η 设置为合适的值是很重要的, 可以通过反复尝试来找到合适的值。