信号与线性系统翻转课堂笔记15——离散LTI系统模型分析
The Flipped Classroom15 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)离散时间信号(序列)的概念,典型的离散时间信号及其特点:单位序列δ(k)、阶跃序列ε(k)、指数序列a^k、正弦/余弦序列cos( ω_0 k)、复指数序列e^(jω_0 k)等,掌握这些离散信号与对应连续信号的联系与区别,掌握正弦序列的周期性判别方法;
(2)离散LTI系统及其差分方程模型;
(3)差分方程的迭代法求解;
(4,重点)掌握离散LTI系统(线性常系数差分方程)的经典法求解方法,理解差分方程特征根对系统自由响应(微分方程齐次解)的影响;
(5,重点)离散系统零输入响应、零状态响应、全响应的求解,注意其中初始条件的使用问题。
二、问题与解答

(*2)根据上一个问题得到的结论,求解习题1.5。

(*3)举例说明如何由差分方程得出其特征方程。差分方程的齐次解(自由响应)和特征根之间是什么关系,这种关系与微分方程的齐次解与特征根的关系有何区别?重点对比讨论两种系统自由响应模态的幅度、频率与特征根的关系。
(*4)如果将离散LTI系统差分方程的特征根表示为复数平面上的点。则根据上一题的结论讨论:①特征根处于复平面什么范围,当k趋近于∞时,系统的自由响应模态幅度是收敛的?②特征根分别为正实数和负实数(即分别在正实轴和负实轴上)时,其自由响应模态的特点有什么不同?③当特征根处于复平面什么范围时,系统的自由响应是一种振荡模态?振荡模态的频率取决于什么?最大振荡频率为多少?
(*5)求解离散LTI系统的零输入响应、零状态响应、全响应时,由初始条件确定待定系数,分别需要如何利用边界条件(k=0之前或者k=0之后的初始值)?如果给定的初始条件与所需边界条件不符,应该如何处理?请结合课件和教材上的例题进行说明。
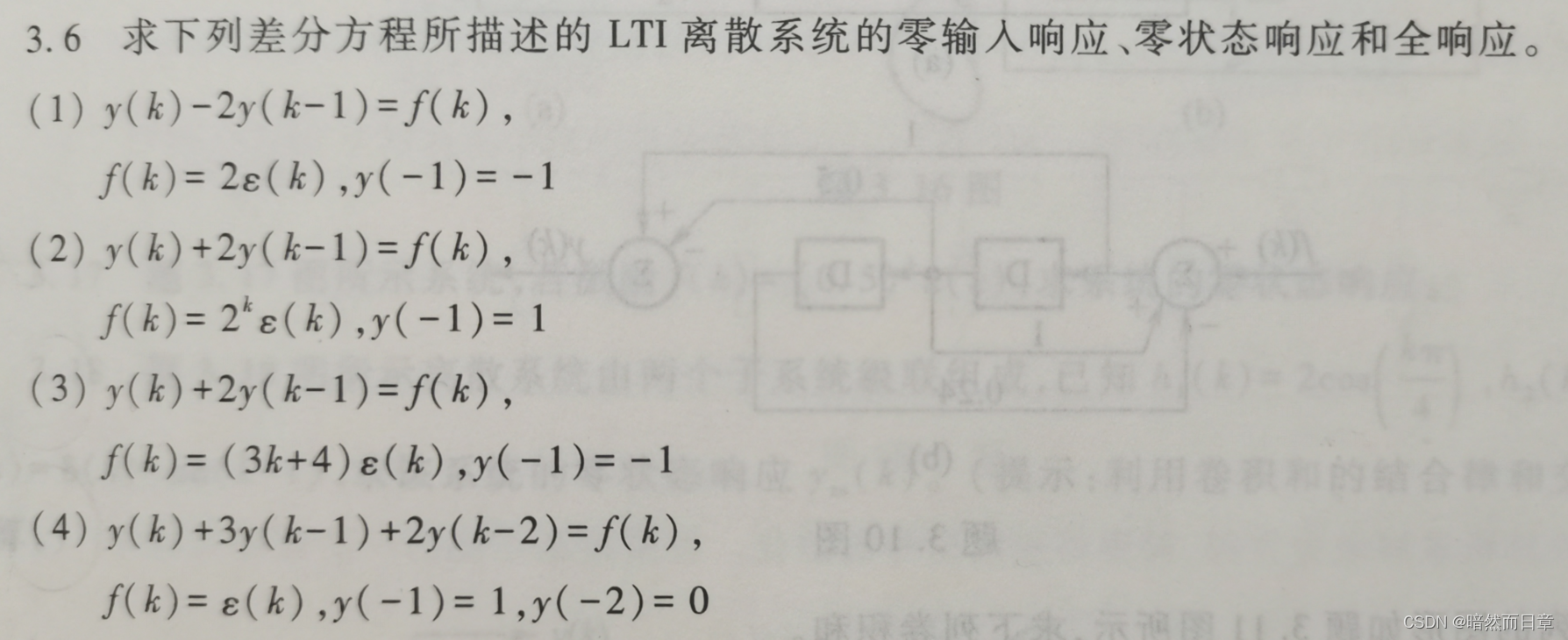
(6)求解习题3.6(4);如果将其中的初始条件改为y(0)=1, y(1)=0,则求解的过程会有什么不同?
1、离散时间信号

单位序列在t=0时取有限值1,在工程实际中存在;单位冲激信号用面积(强度)表示,是面积为1的窄脉冲,T趋近于1时,幅度为无穷,在实际工程中并不存在。单位序列不是单位冲激函数抽样获得。
单位阶跃序列在k>=0时的每个k对应的值定义为1,它可以看做是无数个单位脉冲序列之和;单位阶跃信号是在t=0时发生跃变,与单位冲激信号是微分积分关系。单位阶跃序列与单位序列是和差的关系。
除单位序列,其他离散时间信号都是在连续信号的基础上进行取样形成,连续信号可以看做离散信号的包络。区别在于连续信号在时间上连续,离散信号只在一些离散的瞬间给出函数值,其他时间没有定义。
① 都不是奇异信号,奇异信号或者非奇异信号是针对连续信号而言的,在离散信号中,没有奇异信号这一概念。
②余弦序列不一定为周期信号,复指数序列也不一定为周期信号。正弦序列的周期性判定如下。而复指数信号可以根据欧拉公式写为正余弦序列,当对应的正余弦序列不是周期信号时,这个复指数序列也就不是周期信号了。

③假如连续信号的一个特征根为λ ,则它的齐次解为Ce^λt 的形式;假如离散序列的一个特征根为α,则它的齐次解为Cα^k的形式。表达成这两种不同的形式是为了在求解微分方程、差分方程时能够表示出不同的特性。
2、判断序列的周期性
根据上一个问题得到的结论,求解习题1.5。



3、差分方程与微分方程对比
举例说明如何由差分方程得出其特征方程。差分方程的齐次解(自由响应)和特征根之间是什么关系,这种关系与微分方程的齐次解与特征根的关系有何区别?重点对比讨论两种系统自由响应模态的幅度、频率与特征根的关系。
差分方程:3y(k)-4y(k-1)+y(k-2)=f(k)
特征方程:3λ^2-4λ+1=0
差分方程齐次解和特征根之间关系:

微分方程齐次解和特征根之间关系:

关系:差分/微分方程的齐次解对应于系统的固有响应。特征方程的每一个根对应于固有响应的一个模态,所有特征根所对应模态之和即为系统总的固有响应。
区别:
差分:

微分:

4、特征根于自由响应模态
如果将离散LTI系统差分方程的特征根表示为复数平面上的点。则根据上一题的结论讨论:①特征根处于复平面什么范围,当k趋近于∞时,系统的自由响应模态幅度是收敛的?②特征根分别为正实数和负实数(即分别在正实轴和负实轴上)时,其自由响应模态的特点有什么不同?③当特征根处于复平面什么范围时,系统的自由响应是一种振荡模态?振荡模态的频率取决于什么?最大振荡频率为多少?
①特征根是λ^k的形式,当特征根在半径为1的圆域内时,系统的自由响应模态幅度是收敛的。
②特征根为正实数时是单调的,特征根为负实数时自由响应模态正负交替变化,是振荡的。
③除了正实轴以外,复平面内其他区域,自由响应都是振荡模态。振荡频率取决于相角,最大振荡频率为π。
5、边界条件
求解离散LTI系统的零输入响应、零状态响应、全响应时,由初始条件确定待定系数,分别需要如何利用边界条件(k=0之前或者k=0之后的初始值)?如果给定的初始条件与所需边界条件不符,应该如何处理?请结合课件和教材上的例题进行说明。

零状态响应和全响应需要用k=0之后的初值。零输入响应需要k<0的值。






6、改变初始条件求解离散LTI系统响应
求解习题3.6(4);如果将其中的初始条件改为y(0)=1, y(1)=0,则求解的过程会有什么不同?


三、反思总结
暂无