CGAL的D维包围盒相交计算

包围盒相交测试是一种用于快速判断两个三维对象是否相交的方法，而AABB树则是一种数据结构，常用于加速场景中的射线检测和碰撞检测。

首先，让我们了解一下包围盒相交测试。这种测试的目的是为了快速判断两个三维对象是否相交，而不需要进行细致的几何形状相交测试。常见的包围盒类型包括轴对齐包围盒（Axis-Aligned Bounding Box，简称AABB）和方向包围盒（Oriented Bounding Box，简称OBB）等。

对于两个包围盒是否相交的判断，通常采用分离轴定理（Separating Axis Theorem）进行快速判断。该定理指出，如果两个凸多面体不相交，那么至少存在一个平面，使得这两个多面体在该平面的一侧。因此，对于两个AABB，我们可以分别找到它们各自的六个面，然后判断这些面是否在同一直线上。如果存在同一直线上的两个面，那么这两个AABB必定相交。

接下来，让我们了解一下AABB树。AABB树是由AABB包围盒结点构成的二叉树，常用来加速场景中的射线检测和碰撞检测。树的每个结点都是一个包围盒，且结点的包围盒包裹了所有子结点的包围盒。由于是二叉树，则碰撞查询的时间复杂度是O ( log(n) )。AABB树是一颗满二叉树，对象只存在于叶结点中，父结点的包围盒包含了子结点的包围盒。

在AABB树中进行碰撞检测的基本思路是：首先检测最大的包装盒是否相交（AABB级别），如果相交了，它们可能（注意，只是可能）发生了碰撞，接下来将进一步地递归处理它们（OBB级别），不断地递归用下一级进行处理。如果沿着下一级发现子树并没有发生相交，这时就可以停止，并得出结论没有发生碰撞。如果发现子树相交，那么要进一步处理它的子树直到到达叶子节点，并最终得出结论。

综上所述，包围盒相交测试和AABB树都是计算机图形学中用于提高渲染和碰撞检测效率的重要工具。它们虽然原理和应用有所不同，但都是为了提高三维对象的处理效率而发展出来的技术。

1、介绍

如果基本体不再那么简单，例如三维三角形和多面体表面的小平面，那么关于几何基本体的简单问题，如相交和距离计算，本身可能会变得相当昂贵。因此，在这些基元上操作的算法在实践中往往是缓慢的。一种常见的（启发式）优化方法通过其轴对齐的边界框来近似几何图元，在框上运行适当的算法修改，并且每当一对框具有有趣的交互时，只有在框中包含的复杂几何图元上才能计算出确切的答案。

我们提供了一种有效的算法，用于找到大量等向框的所有相交对，即，通常这些框将是更复杂几何形状的边界框。该算法的一个直接应用是检测多面体表面的所有交点（和自交点），即将该算法应用于空间中的一大组三角形，我们将在本章稍后给出一个示例程序。不太明显的应用是这些曲面之间的邻近性查询和距离计算，请参见第节“使用自定义特征类进行点邻近性搜索的示例”，以及了解更多详细信息。

2、定义

d维等向性盒被定义为d个间隔的笛卡尔积。如果d个间隔{[loi,hii]|0≤i<d}是半开区间，则我们称该盒为半开盒，如果d个间隔{[loi,hii]|0≤i<d}是闭区间，则我们称该盒为闭盒。请注意，闭盒支持零宽度盒，它们可以在其边界处相交，而非空半开盒总是具有正体积，并且只有当它们的内部重叠时才会相交。闭盒和半开盒之间的区别不需要对盒进行不同的表示，只需要在比较盒时进行不同的解释，这是由拓扑参数的两个可能值选择的：

Box_intersection_d:: HALF_OPEN 和 Box_intersection_d:: CLOSED。区间边界的数字类型必须是内置类型 int、unsigned int、double 或 float 之一。

此外，一个盒子有一个唯一的id号。即使盒子具有相同的坐标，它也用于在每个维度上一致地排序盒子。因此，该算法保证一对相交的盒子只被报告一次。请注意，具有相同id号的盒子不会被报告，因为它们显然是相互交叉的。

盒子相交算法有两种形式：一种算法处理单个盒子序列并计算所有成对交集，称为完全情况，例如在自交测试中使用。另一种算法处理两个盒子序列，并计算第一个序列中的盒子与第二个序列中的盒子之间的成对交集，称为二分情况。对于每个发现的成对交集，都会调用一个具有两个参数的回调函数；第一个参数是第一个序列中的盒子，第二个参数是第二个序列中的盒子。在完全情况下，第二个参数是第一个序列的内部副本中的盒子。

3、软件设计

盒交集算法被实现为一个通用函数族；完全情况下的函数接受一个迭代器范围，二分情况下的功能接受两个迭代者范围。用于报告相交对的回调函数是作为BinaryFunction概念的模板参数提供的。使用所有默认参数的两个主要函数调用如下所示：

#include <CGAL/box_intersection_d.h>
template< class RandomAccessIterator, class Callback >
void box_intersection_d(RandomAccessIterator begin,
                        RandomAccessIterator end,
                        Callback callback);
template< class RandomAccessIterator1,
          class RandomAccessIterator2,
          class Callback >
void box_intersection_d(RandomAccessIterator1 begin1, RandomAccessIterator1 end1,
                        RandomAccessIterator2 begin2, RandomAccessIterator2 end2,

函数调用的其他参数是调整性能权衡的截止值，以及在拓扑上封闭的盒子（默认）和拓扑上半开放的盒子之间进行选择的拓扑参数。

该算法在算法过程中对盒子进行重新排序。现在，根据盒子的尺寸，复制盒子或使用指向盒子的指针并仅复制指针可能更快。我们为这两种选项提供自动支持。为了简化描述，让我们将迭代器范围的值类型称为盒子句柄。盒子句柄可以是我们的盒子类型本身，也可以是盒子类型的指针（或 const 指针）；这些选择代表了上述两种选项。

一般来说，这些算法将box类型视为不透明类型，并假设它们是Assignable概念的模型，因此算法可以修改输入序列并重新排列box。对box维度和box坐标的访问是通过BoxIntersection Traits_d概念的traits类来介导的。提供了一个默认的traits类，该类假设box类型是BoxIntersection Box_d概念的模型，并且box句柄，即迭代器值类型，与box类型相同或指向box类型（参见前一段关于box句柄的值与指针特性的描述）。

提供了面向 ISO 的两个实现：Box_intersection_d::Box_d 作为普通盒子，Box_intersection_d::Box_with_handle_d 作为盒子加上一个手柄，可用于指向由盒子近似表示的完整几何体。这两个实现都有模板参数，用于区间边界的数字类型、盒子的固定维度和策略类[1]，用于在提供 ID 编号的多个解决方案中进行选择。

二分情况下的函数签名如下。除了单个迭代器范围之外，带有 box_self_intersection_d() 函数的完整情况的签名看起来是一样的。

#include CGAL/box_intersection_d.h
template< class RandomAccessIterator1,
          class RandomAccessIterator2,
          class Callback >
void box_intersection_d(RandomAccessIterator1 begin1, RandomAccessIterator1 end1,
                        RandomAccessIterator2 begin2, RandomAccessIterator2 end2,
                        Callback callback, std::ptrdiff_t cutoff = 10,
                        Box_intersection_d::Topology topology = Box_intersection_d::CLOSED,
                        Box_intersection_d::Setting setting = Box_intersection_d::BIPARTITE);
template< class RandomAccessIterator1,
          class RandomAccessIterator2,
          class Callback, class BoxTraits >
void box_intersection_d(RandomAccessIterator1 begin1, RandomAccessIterator1 end1,
                        RandomAccessIterator2 begin2, RandomAccessIterator2 end2,
                        Callback callback, BoxTraits box_traits,
                        std::ptrdiff cutoff = 10,
                        Box_intersection_d::Topology topology = Box_intersection_d::CLOSED,
                        Box_intersection_d::Setting setting = Box_intersection_d::BIPARTITE);

4、性能

实现的算法在[2]中被描述为版本二。它的性能取决于一个截止参数。当两个迭代器范围的大小都低于截止参数时，函数将从流分段树算法切换到双向扫描算法，有关详细信息，请参阅[2]。

流式分段树算法需要O（nlogd（n）+k）最坏情况下的运行时间和O（n）空间，其中n是两个输入序列中的盒子数量，d是盒子的（常数）维数，k是输出复杂度，即盒子的成对交集的数量。双向扫描算法需要O（nlog（n）+l）最坏情况下的运行时间和O（n）空间，其中l是一维（使用算法而不是分段树的维度）中成对重叠间隔的数量。注意，l不一定与k有关，并且使用双向扫描算法是一种启发式算法。

不幸的是，我们没有通用的方法来自动确定最佳截止参数，因为它取决于所使用的硬件、回调运行时和段树运行时之间的运行时比率，当然还有要检查的框的数量及其分布。在回调运行时占主导地位的情况下，最好将阈值参数设置得较小。否则，截止值=n--√可以导致可接受的结果。对于分布良好的盒子，论文[2]给出了数千个最佳截断值。无论如何，为了获得最佳运行时间，建议进行一些实验来比较不同的截止参数。

为了证明方框相交可以很快完成，不同的方框序列在总共4到800000个方框的范围内相交。我们使用闭合拓扑的三维默认框，带有浮动坐标，没有额外的数据字段。该算法直接作用于框，而不是作用于指向框的指针。每个方框交叉点都报告给一个空的伪回调。

对于每个盒子集，使用自适应近似来确定接近最优的截止参数。将流传输所需的运行时间与通常的扫描进行比较。在具有4GB主内存的Xeon 2.4GHz上的结果如图91.1所示。对于少数盒子，纯扫描仍然比具有最佳截止的流式传输更快，这只会将盒子集委托给扫描算法。随着盒子越来越多，开销变得不那么重要了。

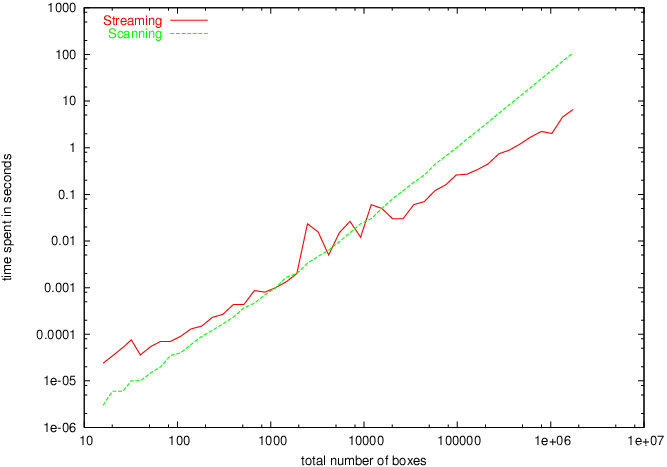
扫描和流算法之间的运行时比较。

5、其他

Box_intersection_d模块提供了一种高效的方式来检测多个三维对象是否相交。它使用了一种基于分离轴定理的算法，通过快速判断两个包围盒是否相交来避免进行繁琐的几何形状相交测试。

在Box_intersection_d模块中，包围盒的类型可以是Axis-Aligned Bounding Box（AABB）或Oriented Bounding Box（OBB）。该模块提供了各种函数和数据结构，用于创建、查询和管理包围盒对象。

此外，Box_intersection_d模块还提供了一些高级功能，如动态更新包围盒、支持不同维度的几何对象等。它还与其他CGAL模块集成，如Mesh_complex、Arrangement等，以提供更完整的几何处理解决方案。

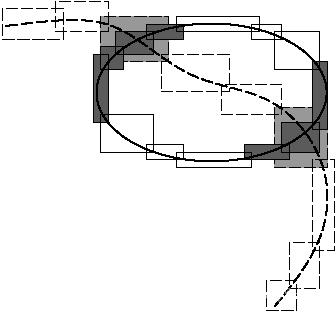
Box_intersection_d::Box_d<double,2> 提供的 box 实现有一个专用的构造函数用于创建 Autorad 包围盒类型 Bbox_2（对于维度 3 也是如此）。我们在我们的最小示例中使用它，在 3×3 的网格布局中轻松创建了九个二维盒子
此外，我们选择中心框和右上角框作为我们的第二个框序列查询。

box类型的默认策略在框中用显式计数器实现id-number，这是默认选择，因为它总是有效，但它会占用空间。

我们使用自己的box类box遵循BoxIntersectionBox_d概念，它允许我们重用默认的traits实现，即，我们可以使用相同的默认函数调用来计算所有交集。

Box_intersection_d::HALF_OPEN：这个常量可能表示盒子的边界是半开放的。在几何学中，一个半开放的边界意味着盒子不包括其边界上的点。例如，考虑一个 2D 盒子，其边界是一个矩形。如果盒子的边界是半开放的，那么矩形的上边和下边是开放的，这意味着它们不包含在盒子的内部。在某些算法和应用中，半开放的边界可能是有用的，因为它允许盒子包含其边界上的点，同时仍然保持盒子的封闭性。

Box_intersection_d::CLOSED：这个常量可能表示盒子的边界是封闭的。这意味着盒子包括其边界上的所有点。在上面的 2D 矩形例子中，如果盒子的边界是封闭的，那么矩形的上边和下边都包含在盒子的内部。在其他算法和应用中，封闭的边界可能是必要的，以确保盒子完全包含其内容。

      Bbox_2 bb = pA[j].bbox() + pA[j+1].bbox();