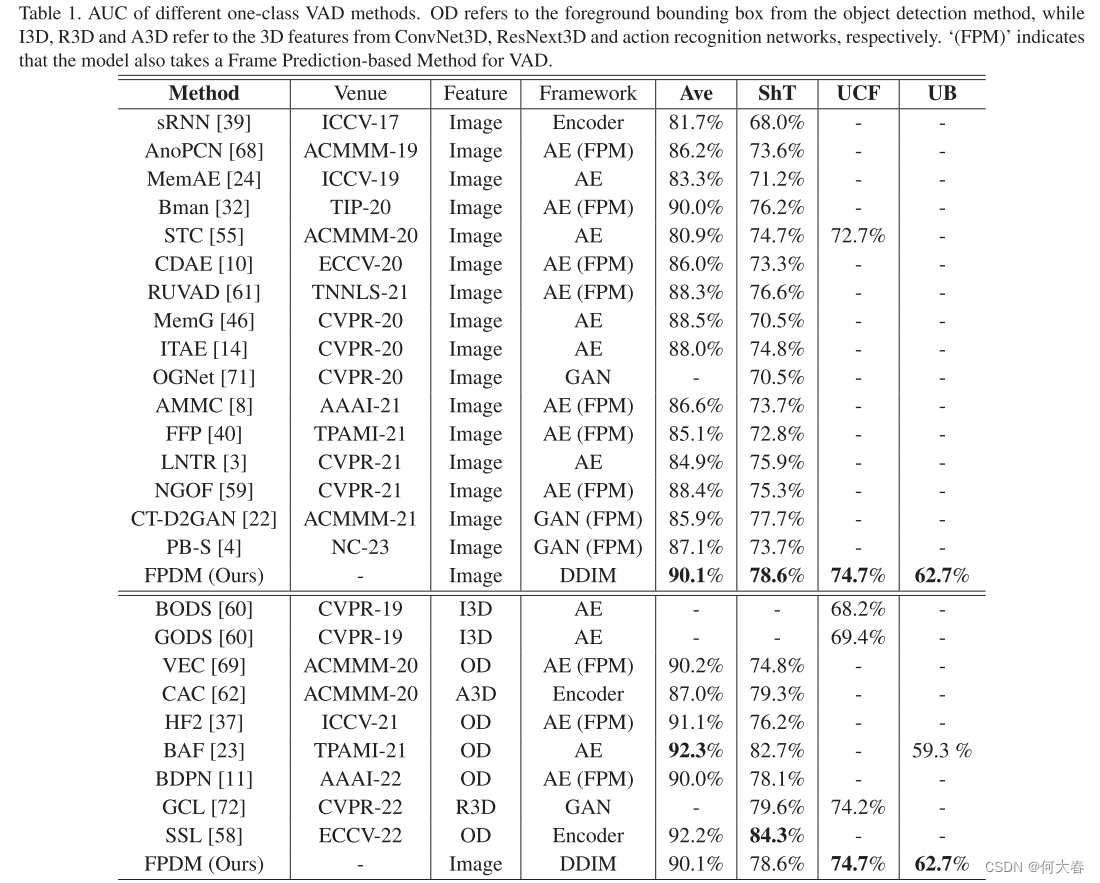
一、动态规划
什么是动态规划?
动态规划(Dynamic Programming,简称DP)是一种解决问题的算法思想,它将一个大问题拆分成多个相互重叠的子问题,并且通过解决这些子问题来求解原始问题
核心思想
拆分大问题为子问题,记住已经解决的子问题,减少重复计算。
二、 从解斐波那契数列看动态规划
这里我们将告诉小伙伴们怎么理解动态规划中的“重复计算”和“记住”,并逐步引出动态规划。
斐波那契数列的特点是数列中的每个数都是由前面两个数相加得到的。例如:1, 1, 2, 3, 5, 8, 13, ...
普通递归求解(自顶向下+自底向上+重复计算)
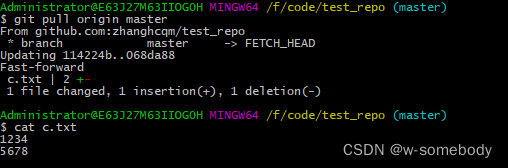
用递归函数来求解就是:
int Fib(int n) { //递归算法1
if (n==1 || n==2){
return 1;
}else{
return Fib(n-1)+Fib(n-2);
}
}对于这个递归函数,求解第五个斐波那契数就是调用Fib(5)。递归过程如下图:
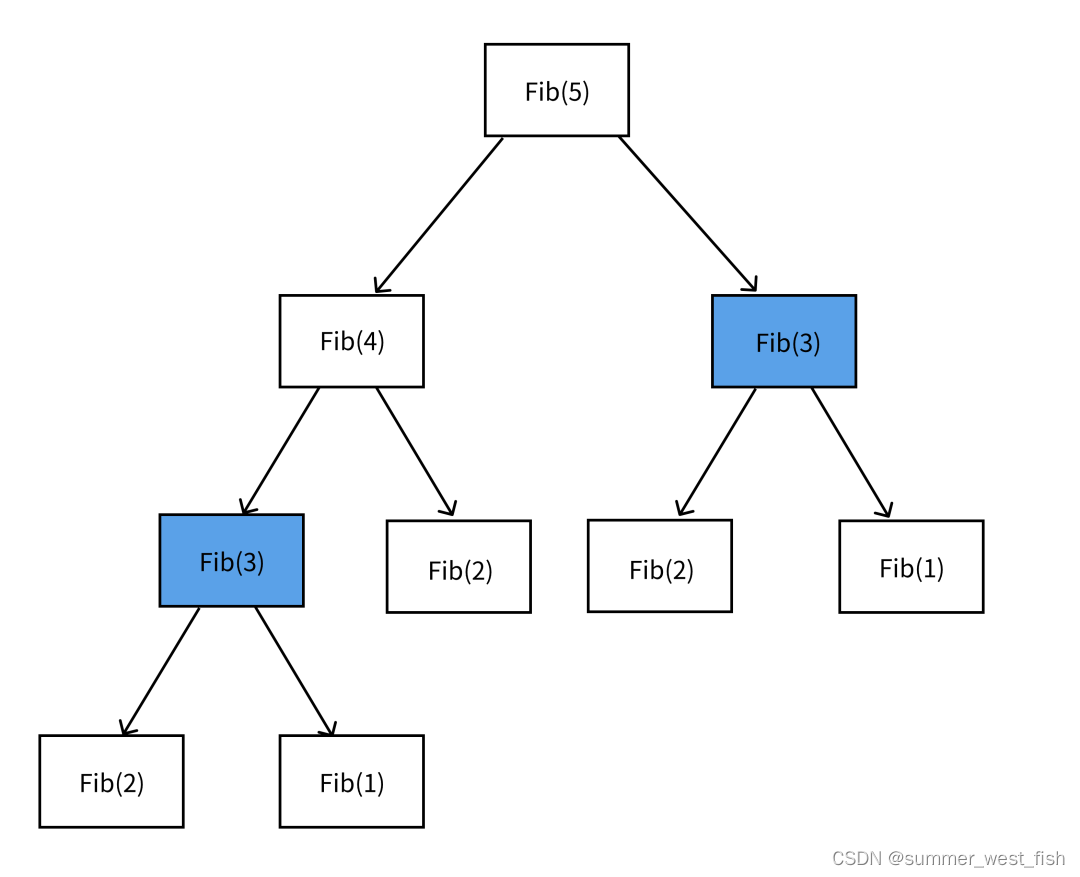
这个普通递归调用Fib(5)采用自顶向下,然后直到调用Fib(2)和Fib(1)后触底反弹,自底向上的执行过程,如上图。
可以看到计算过程中存在大量的重复计算,例如求Fib(5)的过程,如上图蓝色部分存在两次重复计算Fib(3)值的情况,这个就是重复计算,需要我们避免。
备忘录算法求解(自顶向下+自底向上)
我们可以设计一个一维dp数组,用dp[i]存放Fib(i)的值,初始化时数组中所有元素都是-1。对应的算法Fib如下所示:
int Fib(int n) {//带备忘的递归算法
if(n == 0||n == 1) return 1; //递归边界
if(dp[n]!= -1) return dp[n]; //备忘录中有值
else{
dp[n] = Fib1(n-1) + Fib1(n-2); //求得的值存入备忘录
return dp[n];
}
}用数组(或者其他的什么东西)保存已经计算过的子问题,这个过程就叫记忆。是不是很像人常用的备忘录呀~o( ̄▽ ̄)ブ
所以!已经计算过的、得到结果的子问题我们不能忘记!而是要用某种东西保存,让程序“记住”它。这样下次还要用的时候就不用重新计算一下,直接调用即可,节约时间。
就像一位名人说的那样:
Those who cannot remember the past are condemned to repeat it. 忘记过去的人注定会重蹈覆辙。——乔治·桑塔亚纳《常识中的理性》
动态规划法(自底向上)
使用备忘录算法可以避免大量的重复计算。但是我每次使用都需要先从上到下,触底,然后再自底向上返回。这样感觉好累呀😩我能不能就跑一趟呀?本大学生动不了一点。
这就是动态规划!省略自顶向下的过程,直接自底向上!好!就喜欢这种简洁的想法👍
执行过程改变为自底向上,即先求出子问题解,将计算结果存放在一张表中,而且相同的子问题只计算一次,在后面需要时只是简单查表(访问数组,这个数组也叫动态规划数组),以避免重复计算。
算法伪代码如下:
int dp[MAX]; //所有元素初始化为0
int Fib(int n) { //迭代实现
dp[0]=dp[1]=1;
for (int i=2;i<n;i++){
dp[i]=dp[i-1]+dp[i-2]; //计算子问题
}
return dp[n];
}嘶~这个伪代码怎么体现查表的?🤔
很简单,例如求解Fib(5):
-
当i=2,dp[2]=dp[1]+dp[0]=2;
-
当i=4,dp[4]=dp[3]+dp[2]。此时dp[2],也就是第三个斐波那契数之前已经被计算过,被保存在了dp[2],直接查表(访问dp[2])就可以了。
求解Fib(5)时的计算过程如下:
(1)计算出Fib(1)=1
(2)计算出Fib(2)=1
(3)计算出Fib(3)=2
(4)计算出Fib(4)=3
(5)计算出Fib(5)=5
优化(减少空间复杂度)
我们观察到对于每一个斐波那契数,它的数值其实只与它的前两个数的数值有关,我们不需要记录除了这两个数之外的数。因此,用不上那么大的一个数组,只需要两个变量。
int Fib(int n){ //优化动态规划数组,使用两个变量
if(n==1) return 1;
else if(n==2) return 2;
else{
int a=1,b=2,c;
for (int i=3;i<=n;i++){
c=a+b;
a=b;
b=c;
}
return c;
}
}