---

一、牛顿法

1.问题条件

1. 目标函数$f(x)$，求极小值
2. 初始点$x_0$
3. 精度要求e（没有提就是近似0）

2.求解过程

1. 求解一阶雅克比矩阵$\nabla f(x)$和二阶海森矩阵${\nabla }^{2}f(x)$，k=0，
2. 若$\nabla f(x_k)<e$，停止迭代，输出结果，否则k=k+1
3. 求海森矩阵的逆矩阵$G=({\nabla }^{2}f(x_k){)}^{-1}$
4. 当前移动步长$d_k=-G\ast \nabla f(x_k)$
5. 下一个迭代点$x_{k+1}=x_k+d_k$，跳至第二步

3.例子

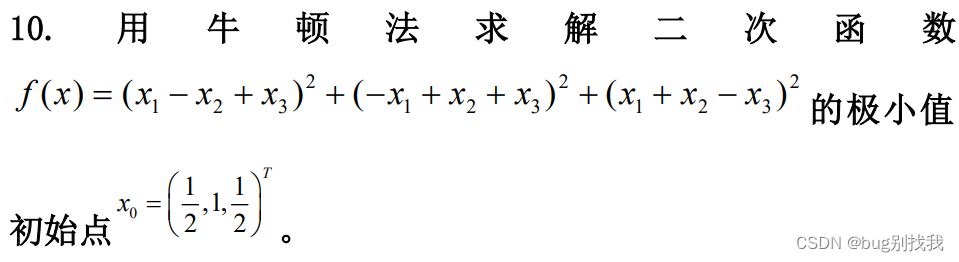
求一阶雅克比矩阵：

$\nabla f(x)=[6x_1-2x_2-2x_3,-2x_1+6x_2-2x_3,-2x_1-2x_2+6x_3){]}^T$

求二阶海森矩阵：

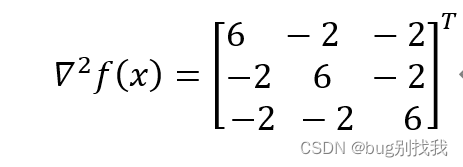
求海森矩阵的逆矩阵G

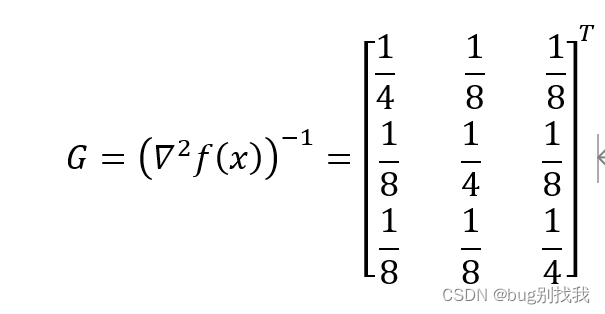
将初始点$x_0$代入$\nabla f(x),{\nabla }^{2}f(x)$得

$\nabla f(x_0)=[0,4,0{]}^T$

${\nabla }^{2}f(x_0)={\nabla }^{2}f(x)$（见上图）

因此 $d_0=-G\ast \nabla f(x_0)=[-1/2,-1,-1/2{]}^T$

则$x_1=x_0+d_0=0$

又因为$\nabla f(x_1)=0$

因此点$x_1$为最优解点，最优解为$f(x_1)=0$

PS

牛顿法通常用于求解目标函数的极小值，如果要求是求目标函数的最大值，将目标函数乘以负号后再按照上述步骤求解即可。