目录
一. 理论部分
二. MATLAB所使用的函数介绍
2.1 概率密度函数
2.2 概率分布函数
2.3 逆概率分布函数
三. 例题与代码
例题1
例题2
例题3
例题4
一. 理论部分
将连续随机变量的概率密度函数记为,既然跟概率相关,那必然满足两个重要的性质:
有时,我们希望求一个范围的概率,这个时候就出现了概率分布函数F(x):
它的物理意义代表着随机变量整个区间所发生的概率。很明显当x越来越大时,包含的概率范围越广,所以PDF函数为单调递增函数。因为概率分布函数也表示与概率相关,所以其值域也在0~1之间:
当x趋近于负无穷大时,代表概率无限小,也就是趋近于0:
当x趋近于无穷大时,代表概率无限大,也就是趋近于1:
二. MATLAB所使用的函数介绍
2.1 概率密度函数
计算概率密度函数值在MATLAB中可直接调用pdf,格式如下:
P=pdf('name',K,A);
P=pdf('name',K,A,B);
P=pdf('name',K,A,B,C);
%name代表概率分布函数名
%K代表求X=K处的概率密度值
%因为不同的分布,相关的参数个数可能不一样,所以有A,B,C比如,在二项分布中,假设一次实验事件Y发生的概率为p。在n次独立重复试验中,事件Y恰好发生K次的概率通常记为,该概率该利用MATLAB进行计算:
p=pdf('bino',K,n,p)
%bino代表二项分布2.2 概率分布函数
根据前面的理论部分,随机变量的概率分布函数可以理解为累积概率值。在MATLAB通常利用"cdf"函数来计算该累积概率值,格式如下:
P=cdf('name',K,A);
P=cdf('name',K,A,B);
P=cdf('name',K,A,B,C);
%name代表概率分布函数名
%K代表当X小于等于K时。这一区间的概率累积值
%因为不同的分布,相关的参数个数可能不一样,所以有A,B,C2.3 逆概率分布函数
如果已知累积分布函数的值,反过来求x的值,则利用逆累积分布函数,在MATLAB调用"icdf",如:
icdf('name',F,A);
icdf('name',F,A,B);
icdf('name',F,A,B,C);
%name代表概率分布函数名
%F代表返回临界值X
%因为不同的分布,相关的参数个数可能不一样,所以有A,B,C换句话说,MATLAB以下代码为互逆过程:
F= cdf('name',X,A,B,C)
X = icdf('name',F,A,B,C)
三. 例题与代码
例题1
计算正态分布N(0,1)的随机变量X在点0.6587的密度函数值。
MATLAB代码:
pdf('norm',0.6578,0,1)
%norm代表正态分布
%0.6578代表X的值
%0代表均值,1代表方差运行结果:
ans =
0.3213
例题2
自由度为8的卡方分布,计算在点2.18处的密度函数值。
MATLAB代码:
pdf('chi2',2.18,8)运行结果:
ans =
0.0363
备注:卡方分布大概长这样
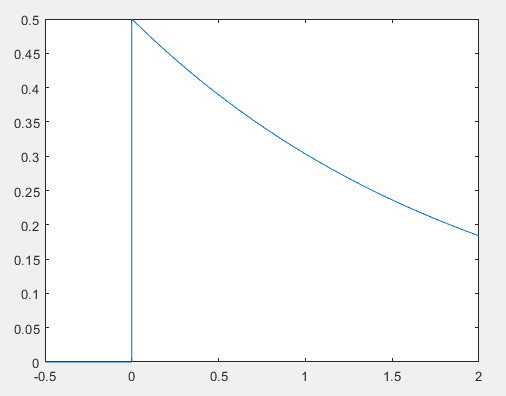
例题3
在标准正太分布表中,若已知F=0.6554,求X。
MATLAB代码:
icdf('norm',0.6554,0,1)运行结果:
ans =
0.3999
例题4
公共汽车门的高度是按成年男子与车门顶碰头的机会不超过1%设计的。设男子身高X(单位:cm)服从正态分布N(175,6),求车门的最低高度。
解:
很明显当车门越高时,头碰撞的概率越低。所以当求车门最低高度时,也就是按恰好头碰撞1%概率来求。
设车门高度为h,X为身高,也就是要求:
MATLAB代码:
h=icdf('norm',0.99, 175, 6)运行结果:
h =
188.9581
计概函数值