转置卷积
转置卷积,顾名思义,通过名字我们应该就能看出来,其作用和卷积相反,它可以使得图像的像素增多
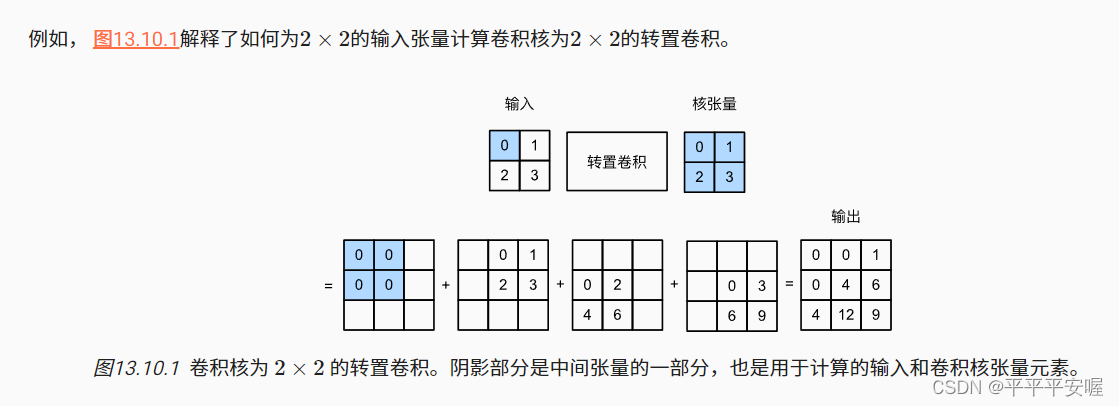
上图的意思是,输入是22的图像,卷积核为22的矩阵,然后变换成3*3的矩阵
代码如下
import torch
from torch import nn
from d2l import torch as d2l
def trans_conv(X, K): #X是原始矩阵,K是转置卷积核
h, w = K.shape
Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1)) # 转置卷积后的大小为x.shape[0] + k.shape[0] - 1 .........
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Y[i: i+h, j: j+w] += X[i, j] * K
return Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)
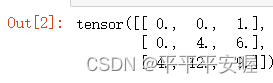
传统输入可能都是四维,使用API一样的
# 四维的话,调用API一样的
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)

与常规卷积不同,在转置卷积中,填充被应用于的输出(常规卷积将填充应用于输入)。
例如,当将高和宽两侧的填充数指定为1时,转置卷积的输出中将删除第一和最后的行与列。
换句话说,转置卷积的padding是删除输出的一圈
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=1, bias=False)
tconv.weight.data = K
tconv(X)

如果步幅为2的话,那么就会是一个4*4的矩阵
# 步幅为2的话那就是4*4了
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, stride=2, bias=False)
tconv.weight.data = K
tconv(X)

对于多个输入和输出通道,转置卷积与常规卷积以相同方式运作。 假设输入有ci个通道,且转置卷积为每个输入通道分配了一个kwkh的卷积核张量。
当指定多个输出通道时,每个输出通道的卷积核shape为cikw*kh
接下来我们可能会想,转置卷积为何以矩阵变换命名呢?我们先来看看矩阵乘法如何实现卷积
这是传统卷积
X = torch.arange(9.0).reshape(3, 3)
K = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
Y = d2l.corr2d(X, K)
Y
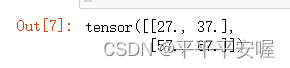
接下来通过矩阵乘法计算
# 先将K 写成稀疏权重矩阵
def kernel2matrix(K):
k, W = torch.zeros(5), torch.zeros((4, 9)) # W是4*9的
k[:2], k[3:5] = K[0, :], K[1, :]
W[0, :5], W[1, 1:6], W[2, 3:8], W[3, 4:] = k, k, k, k
return W
W = kernel2matrix(K)
W

# 然后就是矩阵乘法
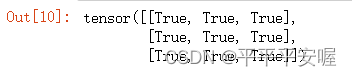
Y == torch.matmul(W, X.reshape(-1)).reshape(2, 2)
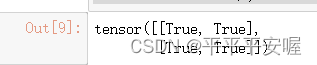
而如果我们用W的转置*Y,那就是原来的Y的转置卷积了
# 同样的,我们可以使用矩阵乘法来实现转置矩阵 Y 是卷积后的值
Z = trans_conv(Y, K)
Z == torch.matmul(W.T, Y.reshape(-1)).reshape(3, 3)