最小二乘法的拟合
最小二乘法是一种常用的统计学方法，用于通过在数据点中找到一条直线或曲线，使得这条直线或曲线与所有数据点的距离平方和最小化。在线性回归中，最小二乘法被广泛应用于拟合一条直线与数据点之间的关系。

对于线性回归，我们希望找到一条直线的方程式 y = mx + b，其中 m 是斜率，b 是截距，使得这条直线与数据点的距离最小。具体而言，我们希望找到使得观测数据点 (xi, yi) 与直线上对应点 (xi, mx + b) 的距离平方和最小的斜率 m 和截距 b。

最小二乘法的基本思想是，通过最小化观测数据点与拟合直线的距离平方和来确定最佳的斜率和截距。该距离可以使用欧几里得距离（即两点之间的直线距离）来衡量。通过最小化距离平方和，可以得到一组最优的斜率和截距，使得拟合直线与数据点的整体偏差最小。

最小二乘法通常使用最小二乘解来计算最佳的斜率和截距。最小二乘解是通过求解一个最小化误差平方和的优化问题而得到的。在线性回归中，最小二乘解可以通过求解正规方程式来获得，即通过求解矩阵方程 (X^T * X) * beta = X^T * y，其中 X 是输入变量矩阵，beta 是待求解的参数向量，y 是输出变量向量。

最小二乘法的拟合结果可以通过各种方式进行评估，例如计算拟合直线与数据点之间的残差和拟合优度等指标。拟合直线的斜率和截距可以提供有关数据点之间关系的定量信息，例如变量之间的相关性、趋势和预测能力等。

总结而言，最小二乘法是一种用于拟合一条直线或曲线与数据点之间关系的统计学方法。在线性回归中，最小二乘法被广泛应用于找到最佳的斜率和截距，以描述数据点之间的线性关系。该方法通过最小化观测数据点与拟合直线之间的距离平方和，提供了一种可靠的方式来分析和预测数据。

基本的数学形式这样子的：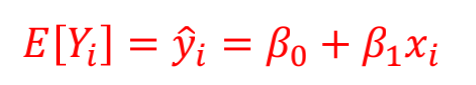

这里我们只需要求出他的两个参数：斜率和截距，这里我们有专门的算法，具体的计算过程如下：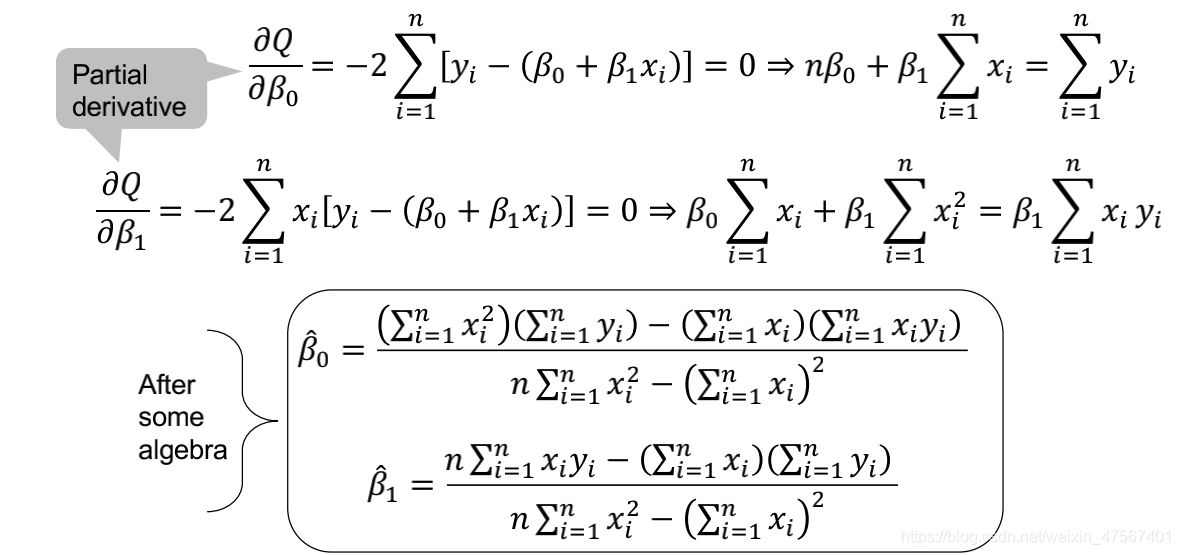

在这里因为计算太复杂了，我们还可以通过一系列的数学化简得到更加简洁的式子：

最后这里就变成了求众多数据点的x、y的一些相乘相加的一些关系。，在这里我用一个组数据作为例子分别用简单的数学计算和矩阵计算来讲解

假设有这么一组数据，这里一共是9个点，我们来看下

x = [0, 4, 8, 12, 16, 20, 24, 28, 32]
y = [394.33, 329.50, 291.00, 255.17, 229.33, 204.83, 179.00, 163.83, 150.33]

我们先来看下第一种简单的数据计算

def calu(x,y,n):#这里输入三个值，x、y和一个有多少组树
#这里我们先定义初始的变量，等会用于求和
        sumx=0
        sumy=0
        smulx=0
        smuly=0
        mulxy=0
#我们要用循环来求和
        for value in range (0,n):
            sumx=sumx+x[value]#求所有x的加和
            sumy=sumy+y[value]
            smulx=smulx+x[value]*x[value]#求所有x的平方和
            smuly=smuly+y[value]*y[value]
            mulxy=mulxy+x[value]*y[value]#求所有x*y的平方和
        avex=sumx/n#求平均值
        avey=sumy/n
        sxx=smulx-(sumx*sumx)/n
        sxy=mulxy-(sumx*sumy)/n
 #求截距和斜率
        m=sxy/sxx
        b=avey-m*avex
        print("y=",m,"x+",b)
        return b,m

这里还有另一个非常巧妙矩阵求法，这里需要掌握一定的线性代数的知识才建议理解和使用，但是非常简洁，线性代数也是在以后在常用的一种数据方式。下面提供一个代码作为参考。

Xt = np.array([np.ones(9),x])
X=Xt.transpose()#求Xt的转置
Y=y.transpose()#求y的转置
Z = np.matmul(Xt,X)#这里是让Xt、x两个矩阵相乘
Zinv=np.linalg.inv(Z)
Z2=np.matmul(Zinv,Xt)
Z3=np.matmul(Z2,Y)
#求矩阵斜率
b = Z3[0]
m = Z3[1]
y=m*x+b

最后我给出这运算的答案以供大家参考