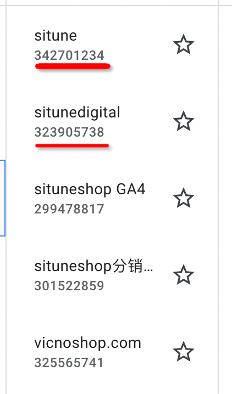
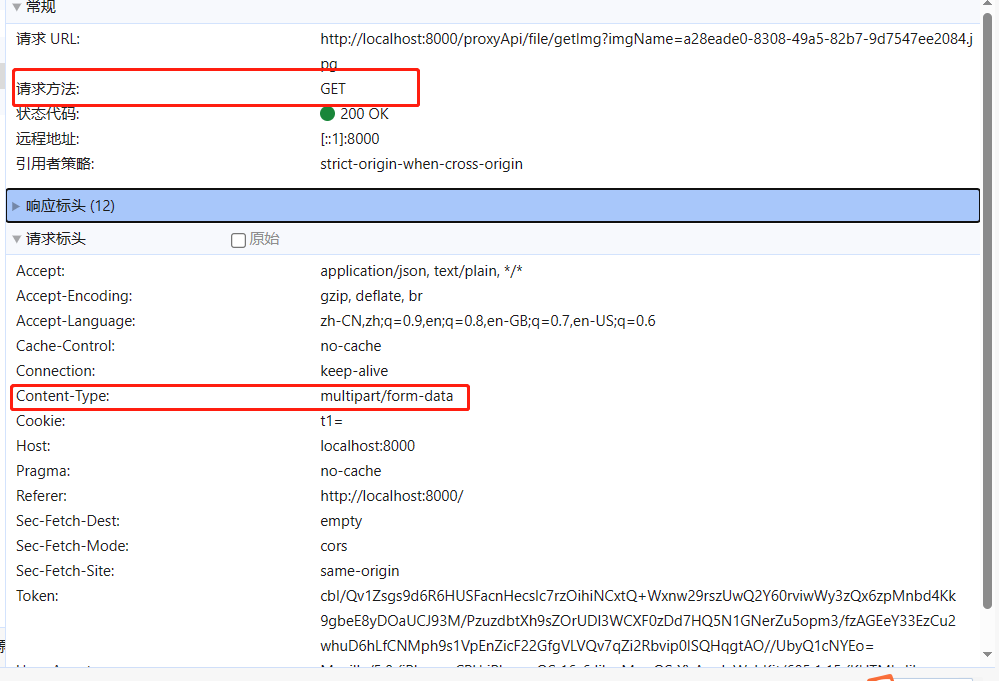
2014年第三届数学建模国际赛小美赛
A题 吹口哨
原题再现:
哨子是一种小装置,当空气被迫通过开口时会发出声音。哨声的巨大而引人注目,使其对警察和体育裁判来说至关重要。当救生员、迷路的露营者或犯罪受害者使用它们时,它们可以挽救生命。专业的口哨需要产生高强度的声音。如何设计世界上最响的口哨?
整体求解过程概述(摘要)
为了解决这一问题,我们提出并评估了两个基本模型。利用有限元分析软件对模型进行求解,得到最优解(理想条件下的最大声强为166 dB左右)。更重要的是,我们创造性地认识到强度受内在和外在因素的影响。在此基础上,以足够合理的参数对实际情况进行了分析。然后,我们可以寻求最优的解决方案,无论具体的要求是不同的应用。此外,我们还对我们的数据和因素,主要是内在参数进行了充分的敏感性分析。
在湍流模型中,基于从开口到末端追踪空气的目的,采用简单的策略来推断声音是如何产生的。提出了一些假设和机理,为后来改进和推广的模型奠定了基础,通过这个模型,我们可以找到一些用于计算声强的数据。一般采用ANSYS来实现该模型。
在气-声转换模型中,首先考虑湍流模型得到的结果,然后计算这些激励参数与最终输出(强度)之间的关系。用近似理论建立方程,计算结果。我们对不同的内在因素进行敏感性分析,以评估我们的策略并找到最优解。采用田口DOE方法进行灵敏度分析,效率更高。
在改进的模型中,首先考虑了基本模型的不足,描述了环境和用户对强度影响较大的实际情况。物理研究的信息是我们分析的基础。由于口哨从民用到军用都有着广泛的应用,因此,我们在模型中引入了策略并解释了机制,从而可以计算出特定条件下模型的最优解。
最后,我们将我们的模型与其他模型进行了比较,并通过仿真进行了验证。我们对我们的模型进行了反思,并对我们的模型在实际情况下能够轻松有效地解决问题进行了评价,但还有一些问题需要进一步完善,例如,吹口哨是一个多目标问题。
模型假设:
假设环境包括温度、湿度是稳定的
假设吹入的空气是理想气体,这意味着没有分子间的相互作用,分子本身不占任何体积。
假设气体的雷诺数为零。
假设该腔体的粗糙度不存在。
假设气体粘度为固定值。
假设腔体不存在变形
假设密封室密封良好
问题重述:
如何估计口哨的整个过程?
声强受多个因素控制,但这几个优化因素尚未明确确定。有必要选择最重要的部分,因为其他部分可能毫无意义。
流体动力学过程是一个复杂的过程,仅仅通过实验是无法得到清晰的结果的。用软件追踪哨声中的空气是最有效的方法。
根据物理学中流体力学的相关知识,不难找到重要元素与声(声)强之间的内在联系,即通过建立数学模型和方程来推导结果。
如何定义最佳配置?
从临界尺度的角度,分析了影响哨声特性的重要因素,包括气压和速度。通过查阅大量的研究资料,我们发现圆形哨声在生活中是普遍存在的,具有优良的性质。因此,我们选择圆度作为基本形状。对于其它工艺参数,基于工艺模拟和正交分析方法,对各参数进行比较后,通过重复模拟进行优化。以形状为主,其他参数可稍后确定。
总体优化
通过仿真计算,得到了圆形哨子的近似最优解。与其他形状(如矩形)相比,圆形口哨是否能发出最大的声音是不确定的。在保持气室比例不变的情况下,改变不同的形状,进行强度分析。
经过一系列的模拟,我们应该找到必要的因素和他们的优先次序,其他可能没有意义的设计一个响亮的口哨。因此,在考虑灵敏度和鲁棒性的基础上,提出了一种新的优化哨子算法。
实际上:声音强度可能会受到外部参数的影响,例如温度、湿度、人的技能。这些参数可能不是由特定的模型计算的,但它们可能对强度有很大的影响。
如果没有可用数据怎么办?
物理问题的目标函数使用机制,社会科学的目标函数使用数据。显然,我们可以从物理和科学论文中获得一些数据。所有模拟和模型都基于这些数据。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
x=linspace(0,1.5,100);
y=(6/9.463822)*x.^(-1)-(1/9.463822)*x.^2;
plot(y,x);
hold on;
plot(0.05*y,x);
hold on;
plot(0.1*y,x);
hold on;
plot(0.2*y,x);
hold on;
plot(0.3*y,x);
hold on;
plot(0.4*y,x);
hold on;
plot(0.5*y,x);
hold on;
plot(0.6*y,x);
hold on;
plot(0.7*y,x);
hold on;
plot(0.8*y,x);
hold on;
plot(0.9*y,x);
hold on;
%plot(0.5*y,x);
%hold on;
%plot(0.5*y,x);
text(0.5,1.5,'')
xlabel('p/p1');
ylabel('U/U*');hold on;
/
x=linspace(0,1.0,100);
y=1.095445115*x.^(1/7);
plot(x,y);
xlabel('p0/p1');
ylabel('c0/U*');hold on;
/
clear all
u=22.12;
a=0.86;
p=101315.39;
k=340/(1.4*u);
w=(a*a)*p*p/(2*2.39*340*(1+k)^2)/10^-12;
db=10*log10(w);
db