一、总体、样本、统计量
总体:在一个统计问题中,我们把研究对象的全体称为总体,构成总体的每个成员称为个体。
样本:在总体中抽取样本的过程称之为抽样,得到样本。
统计量:

二、矩估计
1.矩估计原理
估计的原理就是用计算样本得到的参数替换总体的参数,用样本矩代替总体矩,比如用样本原点矩替换总体原点矩。
2.原点矩与中心距
(1)k阶样本原点矩
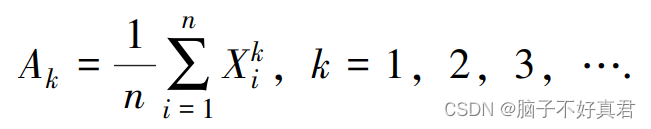
(2)k阶样本中心矩
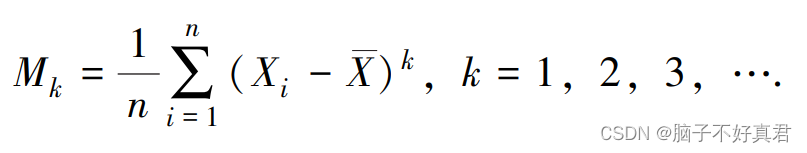
实际上,常用一阶样本原点矩 = 总体E(x),用二阶样本中心矩 = 总体D(x)。
3.离散型随机变量的期望

4.连续型随机变量的期望

5.随机变量的方差
 计算公式:
计算公式:
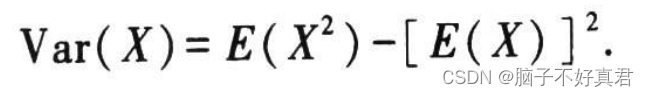
6.六大分布

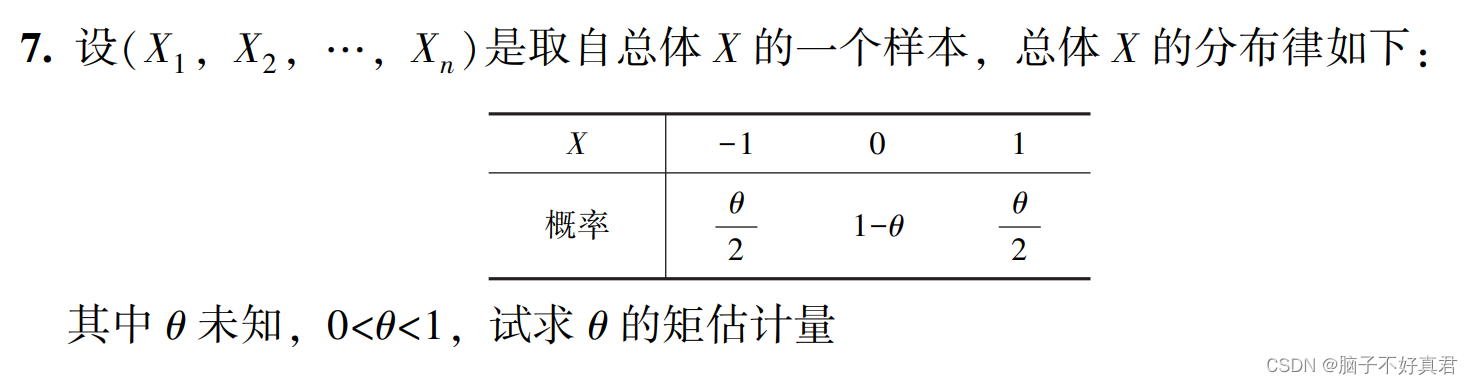
三、例题
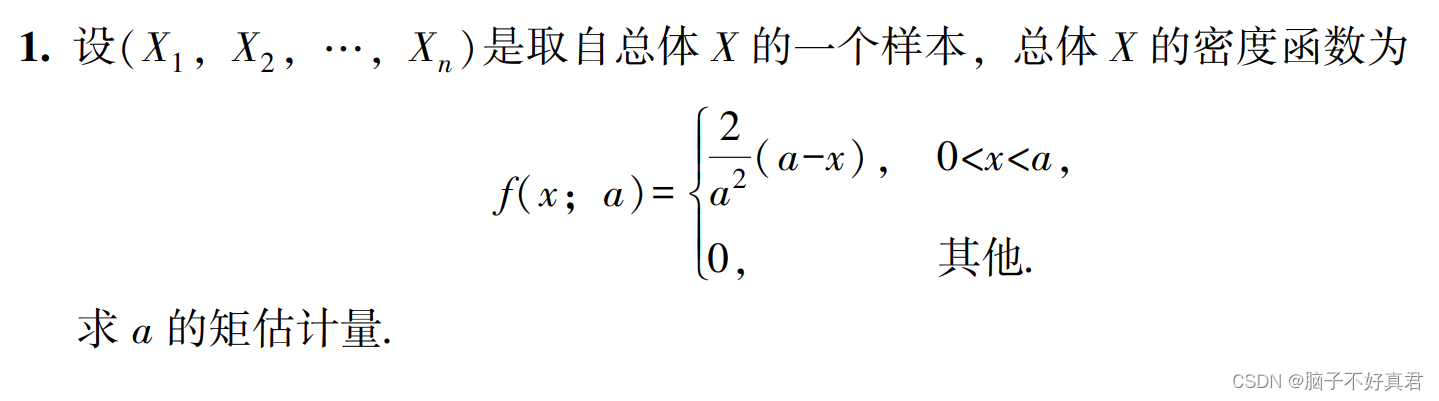



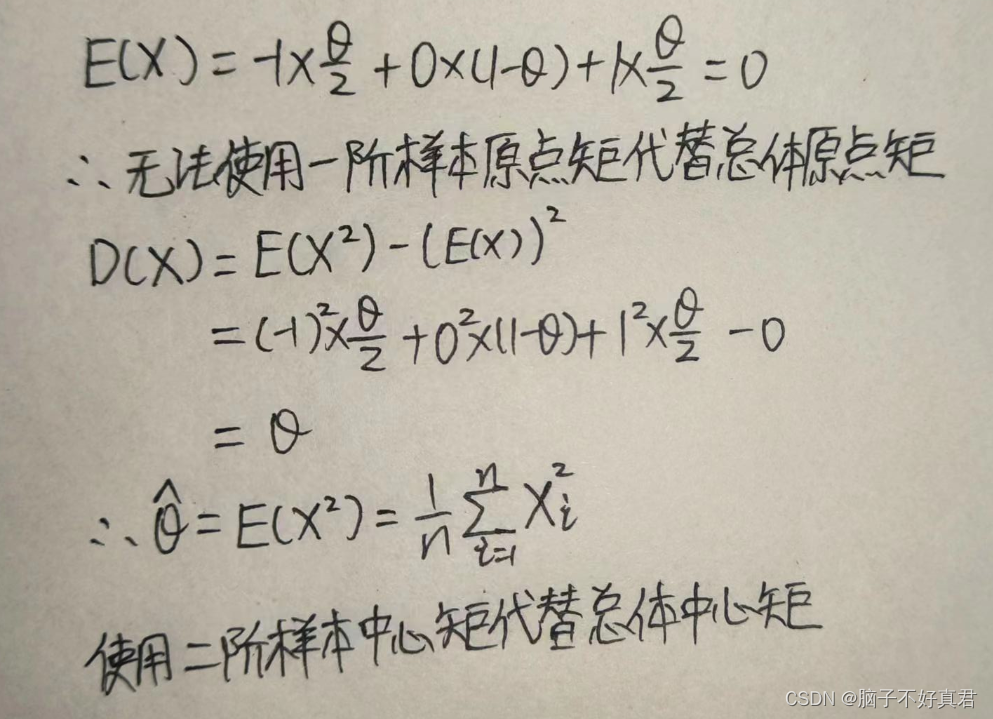
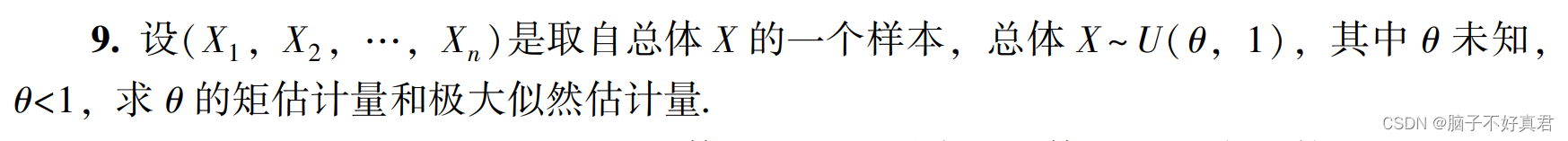


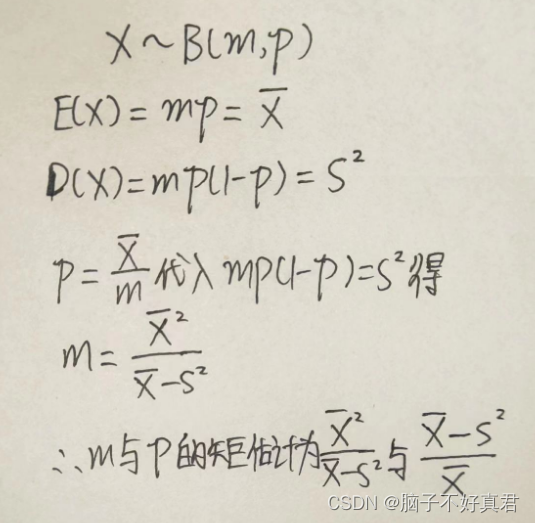
四、参考书目
茆诗松, 周纪芗等. 概率论与数理统计 (第三版). 中国统计出版社, 2007
王松桂等. 概率论与数理统计 (第三版). 科学出版社, 2011
同济大学数学系.概率论与数理统计.人民邮电出版社, 2017