文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:分裂二叉树的最大乘积
出处:1339. 分裂二叉树的最大乘积
难度
6 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,删除一条边将二叉树分裂成两个子树,使得两个子树和的乘积最大。
返回两个子树和的最大乘积。由于答案可能会很大,将结果对 10 9 + 7 \texttt{10}^\texttt{9} + \texttt{7} 109+7 取模后返回。
注意应该在取模前将答案最大化,不是取模后将答案最大化。
示例
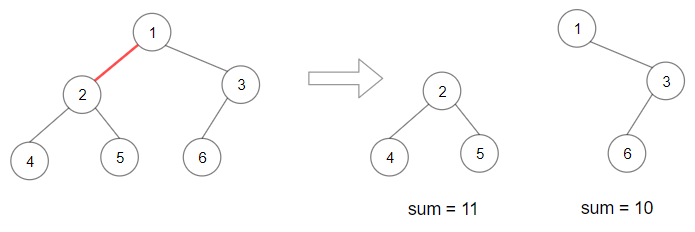
示例 1:
输入:
root
=
[1,2,3,4,5,6]
\texttt{root = [1,2,3,4,5,6]}
root = [1,2,3,4,5,6]
输出:
110
\texttt{110}
110
解释:删除红色的边,得到
2
\texttt{2}
2 个子树,和分别为
11
\texttt{11}
11 和
10
\texttt{10}
10。它们的乘积是
110
\texttt{110}
110(
11
×
10
\texttt{11} \times \texttt{10}
11×10)。
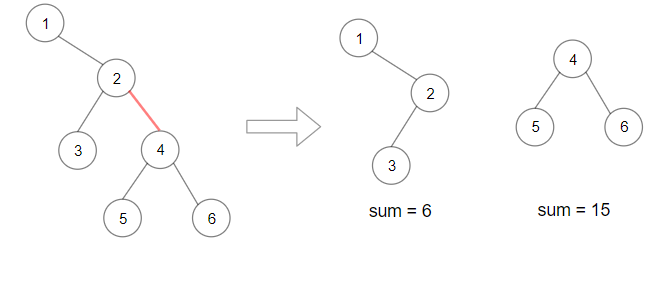
示例 2:
输入:
root
=
[1,null,2,3,4,null,null,5,6]
\texttt{root = [1,null,2,3,4,null,null,5,6]}
root = [1,null,2,3,4,null,null,5,6]
输出:
90
\texttt{90}
90
解释:移除红色的边,得到
2
\texttt{2}
2 个子树,和分别是
15
\texttt{15}
15 和
6
\texttt{6}
6。它们的乘积为
90
\texttt{90}
90(
15
×
6
\texttt{15} \times \texttt{6}
15×6)。
数据范围
- 树中结点数目在范围 [2, 5 × 10 4 ] \texttt{[2, 5} \times \texttt{10}^\texttt{4}\texttt{]} [2, 5×104] 内
- 1 ≤ Node.val ≤ 10 4 \texttt{1} \le \texttt{Node.val} \le \texttt{10}^\texttt{4} 1≤Node.val≤104
解法
思路和算法
删除一条边将二叉树分裂成两个子树之后,其中的一个子树为原二叉树的子树,只要知道二叉树的结点值总和与该子树的结点值总和,即可知道另一个子树的结点值总和并计算两个子树和的乘积。
计算二叉树的结点值总和可以使用深度优先搜索实现。二叉树的结点值总和为根结点与每个非空子树和的总和。
首先计算二叉树的结点值总和,然后再次遍历二叉树计算每个子树的结点值总和。对于每个子树,计算该子树的结点值总和与另一个子树的结点值总和的乘积。遍历结束之后即可得到最大乘积。
二叉树的所有结点值总和不会超出 32 32 32 位整数范围,但是两个子树和的乘积可能超出 32 32 32 位整数范围。为了避免计算最大乘积时溢出,有两种方案,一是使用 64 64 64 位整数存储最大乘积,二是利用数学性质维护最大乘积对应的两个子树和。此处使用第二种方案。
假设原二叉树的结点值总和为 x x x,两个子树和分别为 x 2 + y \dfrac{x}{2} + y 2x+y 和 x 2 − y \dfrac{x}{2} - y 2x−y,其中 x 2 > y > 0 \dfrac{x}{2} > y > 0 2x>y>0,两个子树和的乘积是 ( x 2 + y ) ( x 2 − y ) \Big(\dfrac{x}{2} + y\Big)\Big(\dfrac{x}{2} - y\Big) (2x+y)(2x−y)。根据平方差公式,有 ( x 2 + y ) ( x 2 − y ) = x 2 4 − y 2 \Big(\dfrac{x}{2} + y\Big)\Big(\dfrac{x}{2} - y\Big) = \dfrac{x^2}{4} - y^2 (2x+y)(2x−y)=4x2−y2。由于 x x x 为原二叉树的结点值总和,因此 x x x 为定值,为了使两个子树的乘积最大, y y y 应尽量小,即两个子树和之差的绝对值应尽量小。当两个子树和之差的绝对值最小时,两个子树和的乘积最大。
利用数学性质,维护与二叉树的结点值总和的一半最接近的子树和,遍历结束之后即可得到两个子树和的最大乘积。
代码
class Solution {
static final int MODULO = 1000000007;
int sum = 0;
int bestSplitSum = 0;
public int maxProduct(TreeNode root) {
sum = getSum(root);
getSum(root);
int product = (int) ((long) bestSplitSum * (sum - bestSplitSum) % MODULO);
return product;
}
public int getSum(TreeNode node) {
int curSum = node.val;
TreeNode left = node.left, right = node.right;
if (left != null) {
curSum += getSum(node.left);
}
if (right != null) {
curSum += getSum(node.right);
}
if (sum > 0 && Math.abs(curSum * 2 - sum) < Math.abs(bestSplitSum * 2 - sum)) {
bestSplitSum = curSum;
}
return curSum;
}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。需要执行两次深度优先搜索,每次深度优先搜索的时间复杂度是 O ( n ) O(n) O(n)。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是递归调用的栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。

![[环境配置]win10关闭病毒和威胁防护防止乱删软件](https://img-blog.csdnimg.cn/direct/86ef7815d474446d9f35e2bc39f3c01a.jpeg)