深度学习中的Dropout

1 Dropout概述

1.1 什么是Dropout

在2012年，Hinton在其论文《Improving neural networks by preventing co-adaptation of feature detectors》中提出Dropout。当一个复杂的前馈神经网络被训练在小的数据集时，容易造成过拟合。为了防止过拟合，可以通过阻止特征检测器的共同作用来提高神经网络的性能。

在2012年，Alex、Hinton在其论文《ImageNet Classification with Deep Convolutional Neural Networks》中用到了Dropout算法，用于防止过拟合。并且，这篇论文提到的AlexNet网络模型引爆了神经网络应用热潮，并赢得了2012年图像识别大赛冠军，使得CNN（Convolutional Neural Networks, CNN）成为图像分类上的核心算法模型。

随后，又有一些关于Dropout的文章《Dropout:A Simple Way to Prevent Neural Networks from Overfitting》、《Improving Neural Networks with Dropout》、《Dropout as data augmentation》。

从上面的论文中，我们能感受到Dropout在深度学习中的重要性。那么，到底什么是Dropout呢？

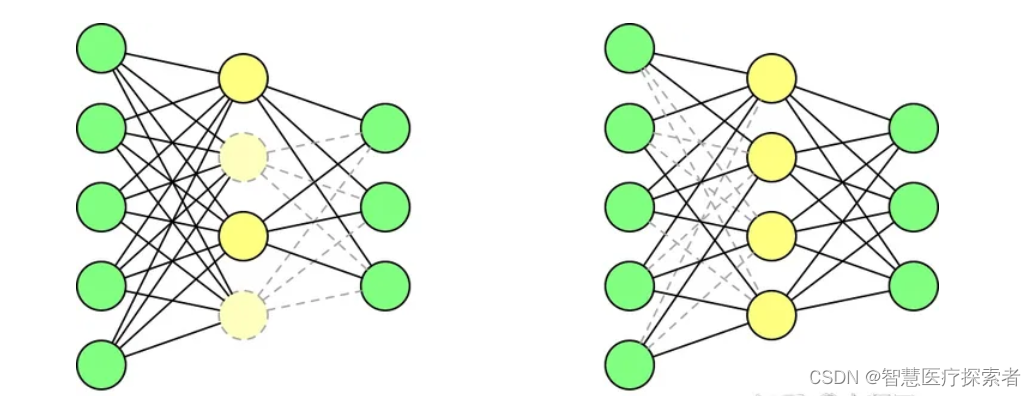
Dropout可以作为训练深度神经网络的一种trick供选择。在每个训练批次中，通过忽略一半的特征检测器（让一半的隐层节点值为0）（不止可以选择一半，也可以选择其他比例），可以明显地减少过拟合现象。这种方式可以减少特征检测器（隐层节点）间的相互作用，检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。

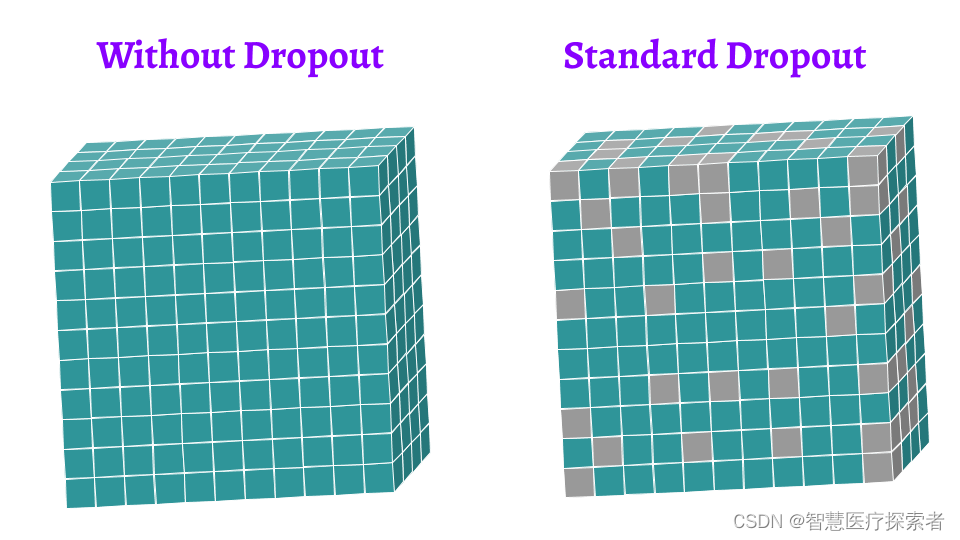
Dropout说的简单一点就是：我们在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征，如图所示。

1.2 Dropout的作用

在机器学习的模型中，如果模型的参数太多，而训练样本又太少，训练出来的模型很容易产生过拟合的现象。在训练神经网络的时候经常会遇到过拟合的问题，过拟合具体表现在：模型在训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。

过拟合是很多机器学习的通病。如果模型过拟合，那么得到的模型几乎不能用。为了解决过拟合问题，一般会采用模型集成的方法，即训练多个模型进行组合。此时，训练模型费时就成为一个很大的问题，不仅训练多个模型费时，测试多个模型也是很费时。

综上所述，训练深度神经网络的时候，总是会遇到两大缺点：

容易过拟合
费时

Dropout可以比较有效的缓解过拟合的发生，在一定程度上达到正则化的效果。

1.3 Dropout的数学原理

一个线性的神经网络，如下图所示，它的输出是输入的加权和，表示为式(1)。这里我们只考虑最简单的线性激活函数，这个原理也适用于非线性的激活函数，只是推导起来更加复杂。

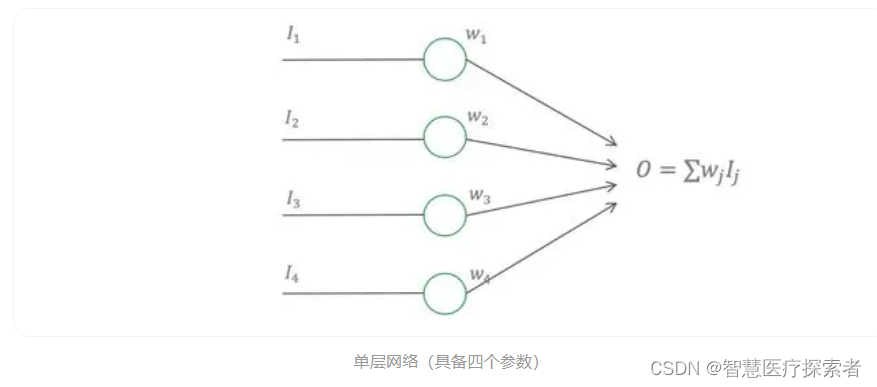
对于上图的无Dropout的网络，它的误差可以表示为式(2)，其中 t 是目标值。

(2)式之所以使用 w‘是为了找到之后要介绍的加入Dropout的网络的关系，其中 w‘=pw 。那么(2)可以表示为式(3)。

关于 $w_{i}$ 的导数表示为（4）

当我们向图2中添加Dropout之后，它的误差表示为式(5)。在这里插入图片描述
是丢失率，它服从伯努利分布，

即它有 p 的概率值为 1，1−p 的概率值为0 。

它关于 $w_{i}$ 的导数表示为（6）

对比式（6）和式（7）我们可以看出，在 $w^{'}=pw$ 的前提下，带有Dropout的网络的梯度的期望等价于带有正则的普通网络。换句话说，Dropout起到了正则的作用，正则项为 $w_{i}p_{i}(1-p_{i})I_{i}^{2}$

1.4 Dropout是一个正则网络

通过上面的分析我们知道最小化含有Dropout网络的损失等价于最小化带有正则项的普通网络，如式(8)。

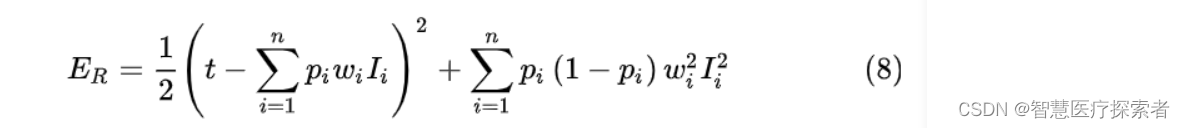
也就是说当我们对式(8)的 $w_{i}$ 进行求偏导，会得到(4)式的带有Dropout网络对 $w_{i}$ 的求偏导相同的结果。因此可以得到使用Dropout的几个技巧：

当丢失率为0.5 时，Dropout会有最强的正则化效果。因为 p(1-p)在 p=0.5时取得最大值。
丢失率的选择策略：在比较深的网络中，使用 0.5的丢失率是比较好的选择，因为这时Dropout能取到最大的正则效果；在比较浅层的网络中，丢失率应该低于 0.2，因为过多的丢失率会导致丢失过多的输入数据对模型的影响比较大；不建议使用大于 0.5的丢失率，因为它在丢失过多节点的情况下并不会取得更好的正则效果。
在测试时需要将使用丢失率对w进行缩放：基于前面 w‘=pw的假设，我们得知无Dropout的网络的权值相当于对Dropout的网络权值缩放了 1-p倍。在含有Dropout的网络中，测试时不会丢弃节点，这相当于它是一个普通网络，因此也需要进行 1-p倍的缩放。

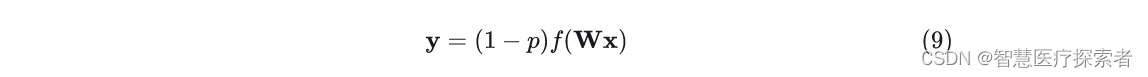
2 Dropout的使用

2.1 CNN的Dropout

不同于MLP的特征层是一个特征向量，CNN的Feature Map是一个由宽，高，通道数组成的三维矩阵。按照传统的Dropout的理论，它丢弃的应该是Feature Map上的若干个像素点，但是思想方法在CNN中并不是十分奏效的，一个重要的原因便是临近像素点之间的相似性。因为他们不仅在输入的值上非常接近，而且他们拥有相近的邻居，相似的感受野以及相同的卷积核。因此Dropout在CNN上也有很多优化。

在CNN中，我们可以以通道为单位来随机丢弃，这样可以增加其它通道的建模能力并减轻通道之间的共适应问题，这个策略叫做Spatial Dropout [6]。我们也可以随机丢弃Feature Map中的一大块区域，来避免临近像素的互相补充，这个方法叫做DropBlock[7]。还有一个常见的策略叫做Max-pooling Dropout [8]，它的计算方式是在执行Max-Pooling之前，将窗口内的像素进行随机mask，这样也使的窗口内较小的值也有机会影响后面网络的效果。

2.2 RNN的Dropout

和CNN一样，传统的Dropout并不能直接用在RNN之上，因为每个时间片的Dropout会限制RNN保留长期记忆得能力，因此一些专门针对RNN的Dropout被提了出来，针对RNN上的Dropout的研究主要集中在LSTM上。RNNDrop[9]提出我们可以在RNN的循环开始之前生成一组Mask，这个mask作用到LSTM的cell states上，然后在时间片的循环中保持这一组Mask的值不变，如式(10)。

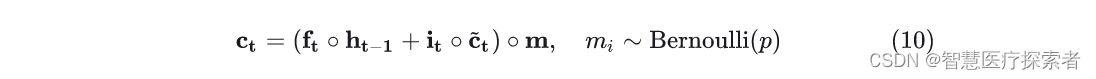
Recurrent Dropout [10]则提出也可以将掩码作用到更新cell state的地方，同样它的掩码值也保持不变，如式(11)。

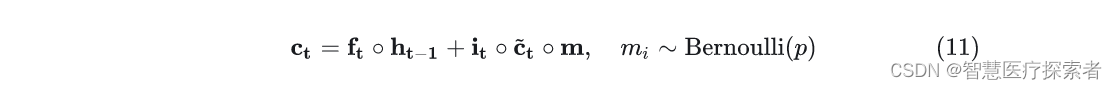
Yarin Gal等人提出Dropout也可以作用到LSTM的各个们上[11]，如式(12)。

其中 $z_{x}$ 和 $z_{h}$ 是作用到输入数据和隐层节点状态的两个掩码，它们在整个时间步骤内保持不变。

2.3 高斯Dropout

在传统的Dropout中，每个节点以 1-p的概率被mask掉。反应到式(5)中，它表示为使用权值乘以 $\delta$ ， $\delta \sim Bernoulli(p)$ 服从伯努利分布。式(5)相当于给每个权值一个伯努利的Gate，如图4所示。
Dropout可以看做给每个权值添加一个伯努利的gate

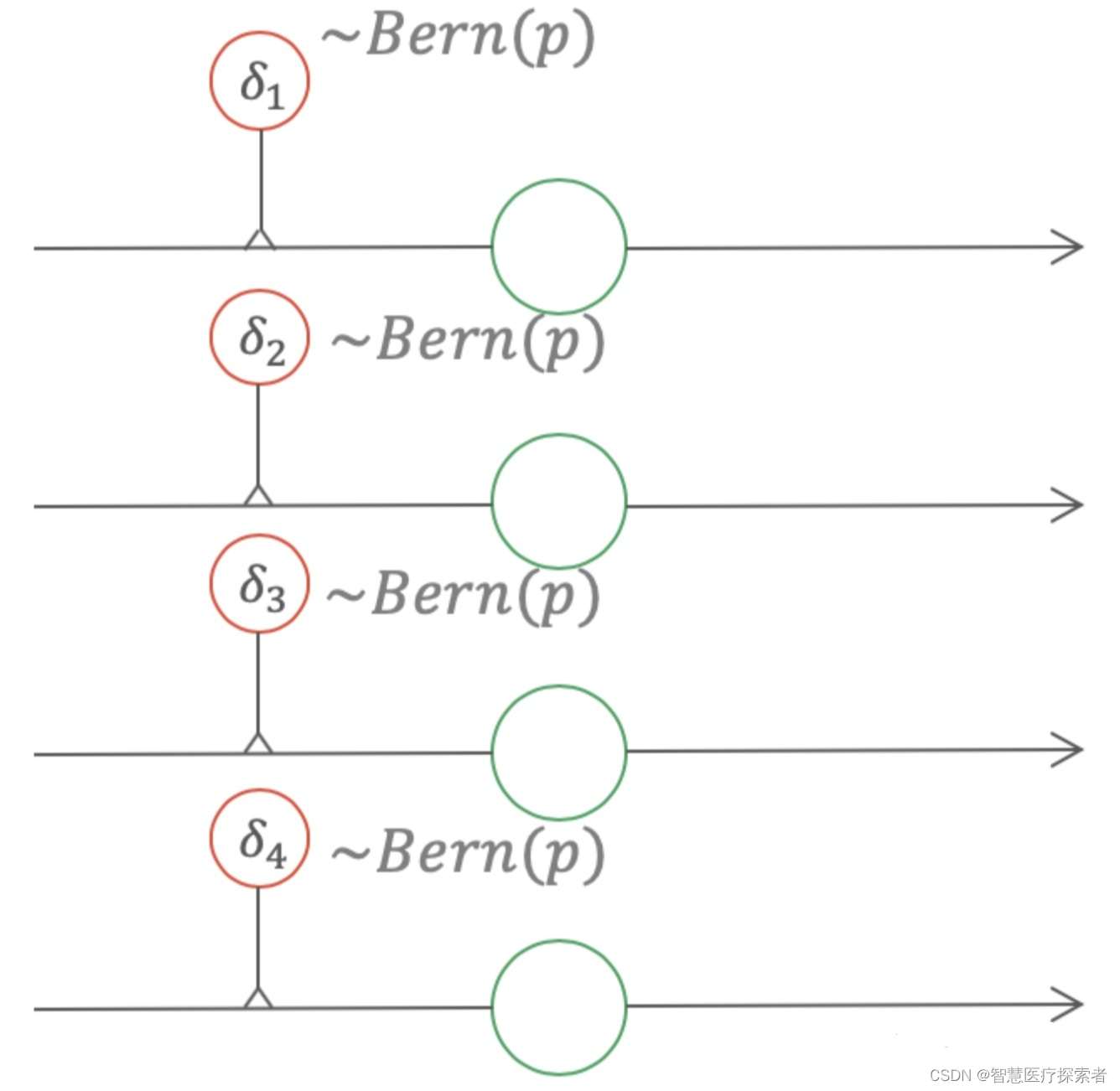
如果将图4中的伯努利gate换成高斯gate，那么此时得到的Dropout便是高斯Dropout，如图5所示。在很多场景中，高斯Dropout能够起到等价于甚至高于普通Dropout的效果。
高斯Dropout

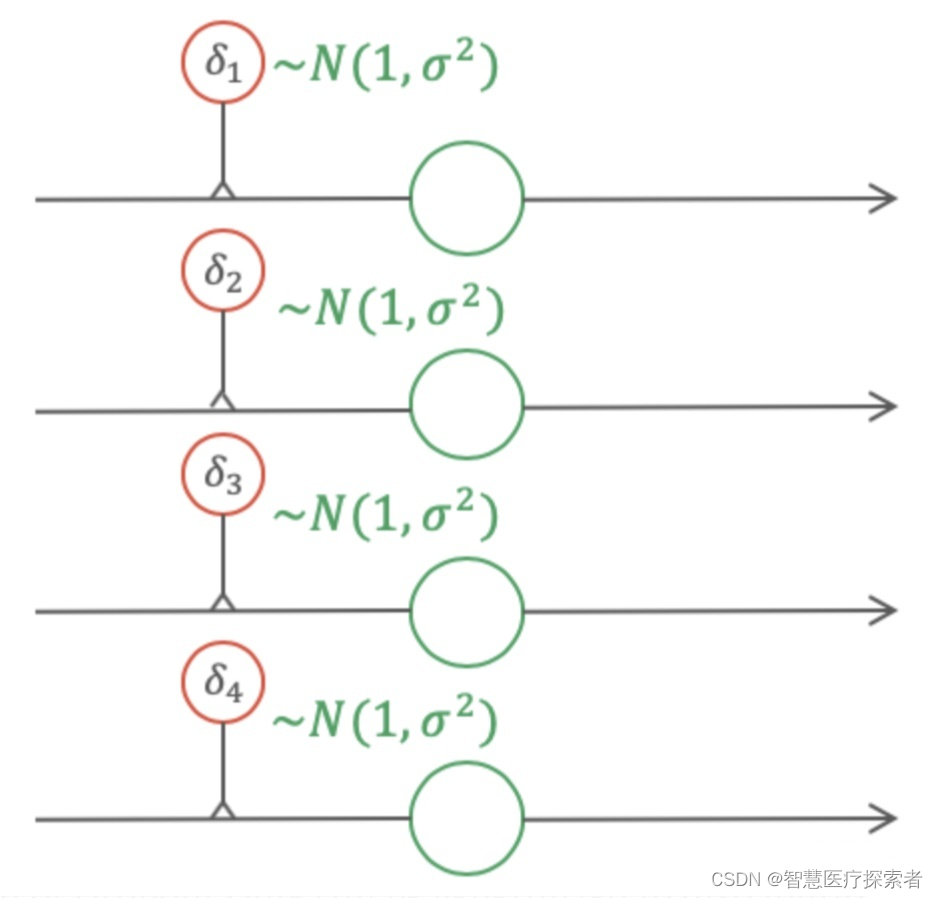
在使用高斯Dropout时，因为激活值保持不变，因此高斯Dropout在测试时不需要对权重进行缩放。因为在高斯Dropout中，所有节点都参与训练，这样对提升训练速度也有帮助。在高斯Dropout中，每个节点可以看做乘以了p(1-p) ，这相当于增熵，而Dropout丢弃节点的策略相当于减熵。在Srivastava等人的论文中，他们指出增熵是比减熵更好的策略，因此高斯Dropout会有更好的效果。

2.4 DropConnect

DropConnect[3]的思想也很简单，它不是随机将隐层节点的输出置，而是将节点中的每个与其相连的输入权值以一定概率置，它们一个是输出，一个是输入，表示为式(13)。

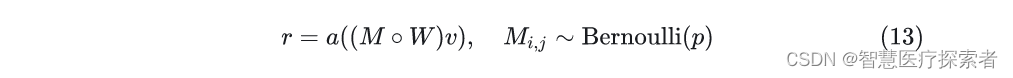
其中M是二值掩码矩阵，它里面的每一个元素服从伯努利分布。Dropout可以看做是对计算完成结果进行掩码，而DropConnect可以看做对输入权值的进行掩码，如图5所示。

2.5 StandOut

在Dropout中，每个节点以相同概率的伯努利分布被丢弃，StantOut[4]提出丢弃的概率应该是自适应的，它的值取决于权重的值，一般权重越大，被丢弃的概率越高。在训练时，StandOut的节点被丢弃的概率表示为式(14)。

其中 $W_{s}$ 是网络权值， $g$ 是激活函数，也可以是一个网络，例如深度置信网络。实验结果表明深度置信网络可以近似为权重的仿射函数，例如我们可以采用sigmoid激活函数。在测试的时候，我们也需要对权值进行缩放。

在StandOut中，一个节点被mask掉的概率取决于它的权值，权值越高它被mask掉的概率越高，这样就避免了网络过分依赖某些少数的节点。

2.6 蒙特卡洛Dropout

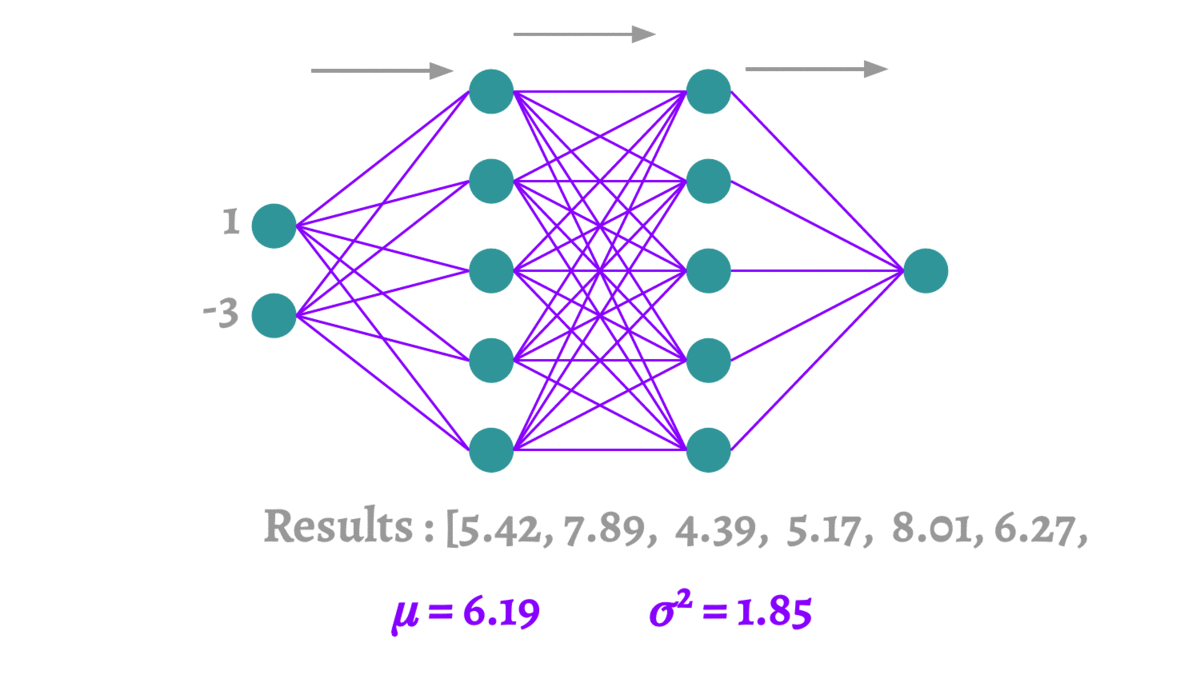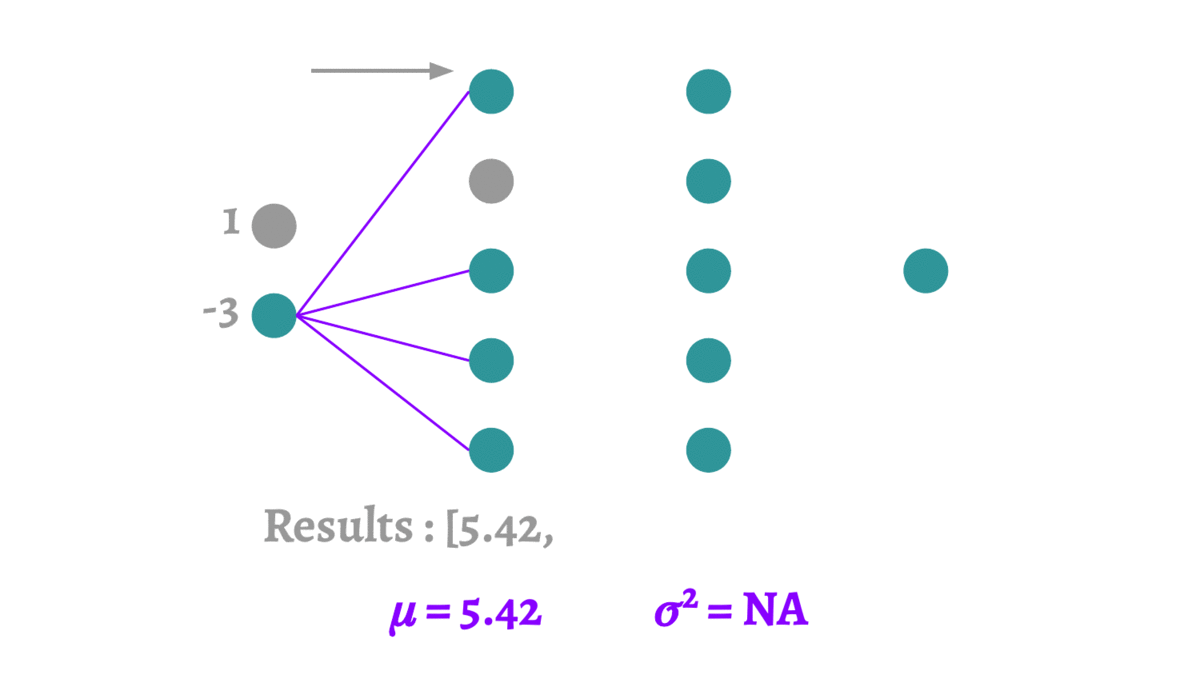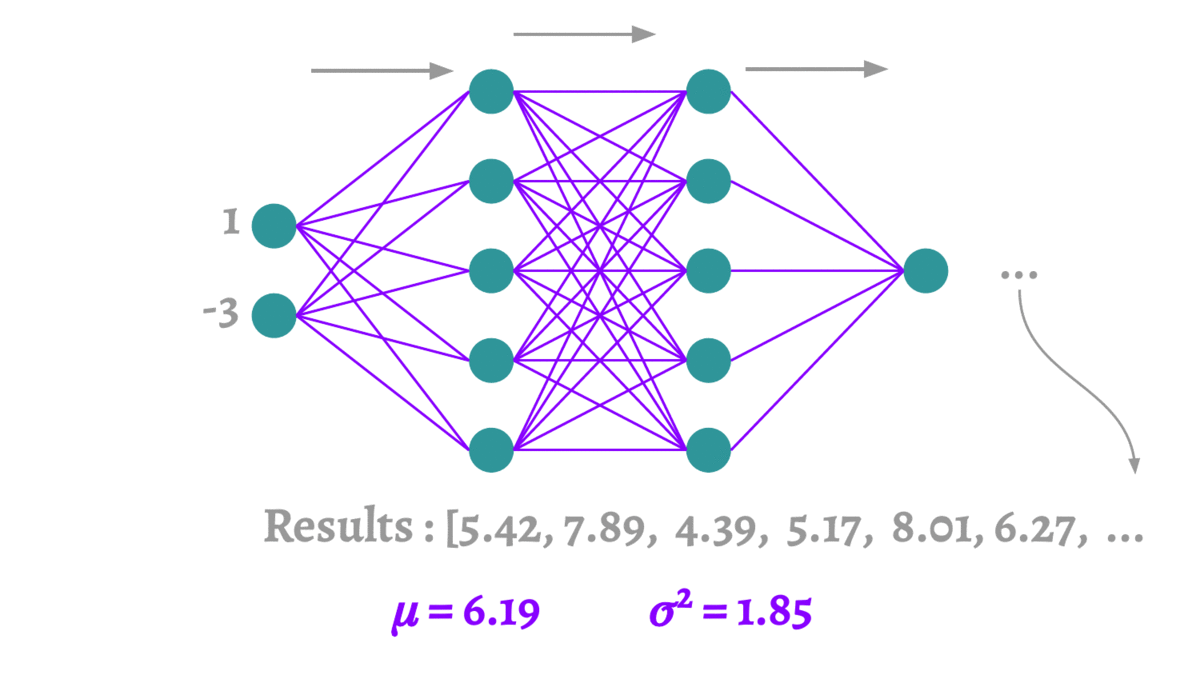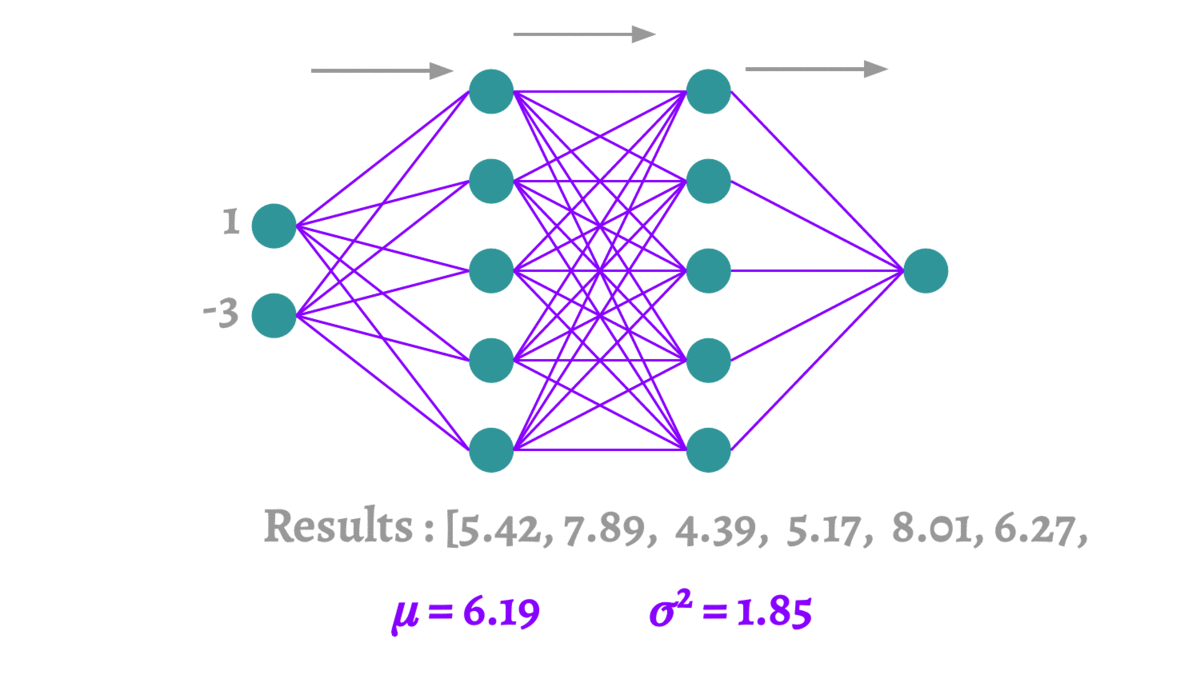
蒙特卡洛方法本质上是通过有限次的采样，来拟合一个测试结果。这里要介绍的蒙特卡洛Dropout（MCDropout）[12]可以使用到任何使用Dropout训练的网络中，在训练时MCDropout和原始的Dropout保持相同，但是在测试时它继续保留Dropout的丢弃操作，通过随机采样大量不同的测试结果来产生真实的结果，得到预测结果的均值和方差。因为MCDropout的多次预测是可以并行执行的，因此并不会耗费太长的时间。

论文中MCDropout的理论证明非常复杂，这里我们大致阐述一下它的思想。MCDropout的提出思想主要是作者认为softmax的值并不能反映样本分类的可靠程度。跟我我们对softmax输出向量的观察，值最大的那一类往往是一个非常高的一个值，甚至当它预测错误的时候这个值也有可能大于

，这个值作为模型的置信度是非常不可靠的。MCDropout通过在不同的模型上的采样来对同一个数据进行预测，那么根据多次采样的结果便可以得到一个比softmax更可靠的置信度。恰好Dropout是一个天然的不同模型的生成器，所以在测试的时候要保留Dropout。

3 Dropout的代码实现

import numpy as np
 
def dropout(x, keep_prob):
    d3 = (np.random.rand(*x.shape) < keep_prob)  #dropout
    print(d3)
    x = np.multiply(x,d3)
    print(x)
    x = x/keep_prob  #inverted dropout
    return x
 
a3 = np.asarray([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=np.float32)
a3 = dropout(a3,0.8)
print(a3)