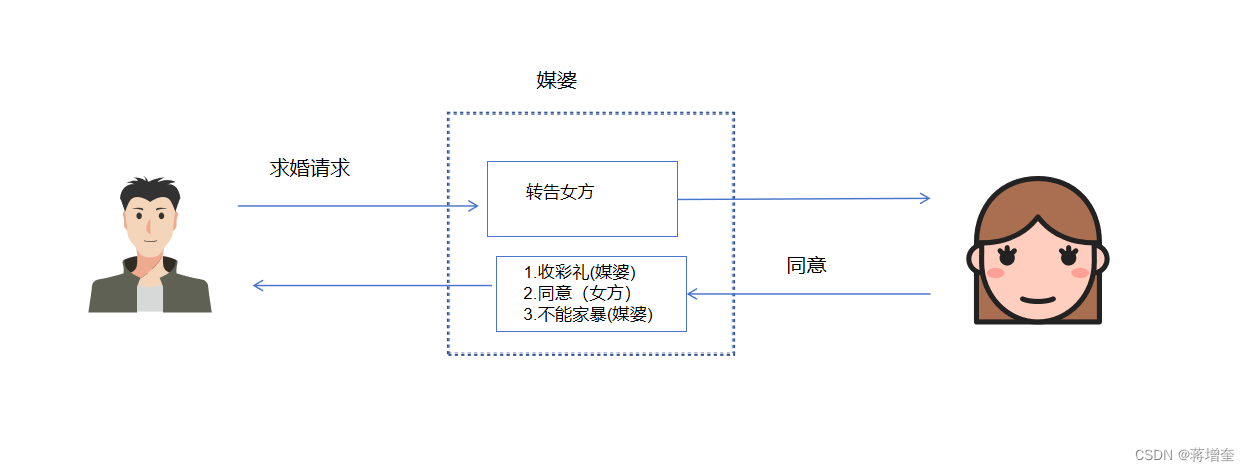
满足条件的01序列

假设长度为n个序列要求满足题意1的前缀0的个数不能超过1的个数
将问题抽象为从(0, 0)到(n, n)
向上走一个代表这一步对应序列中的值是1，向右走代表序列中的值是0

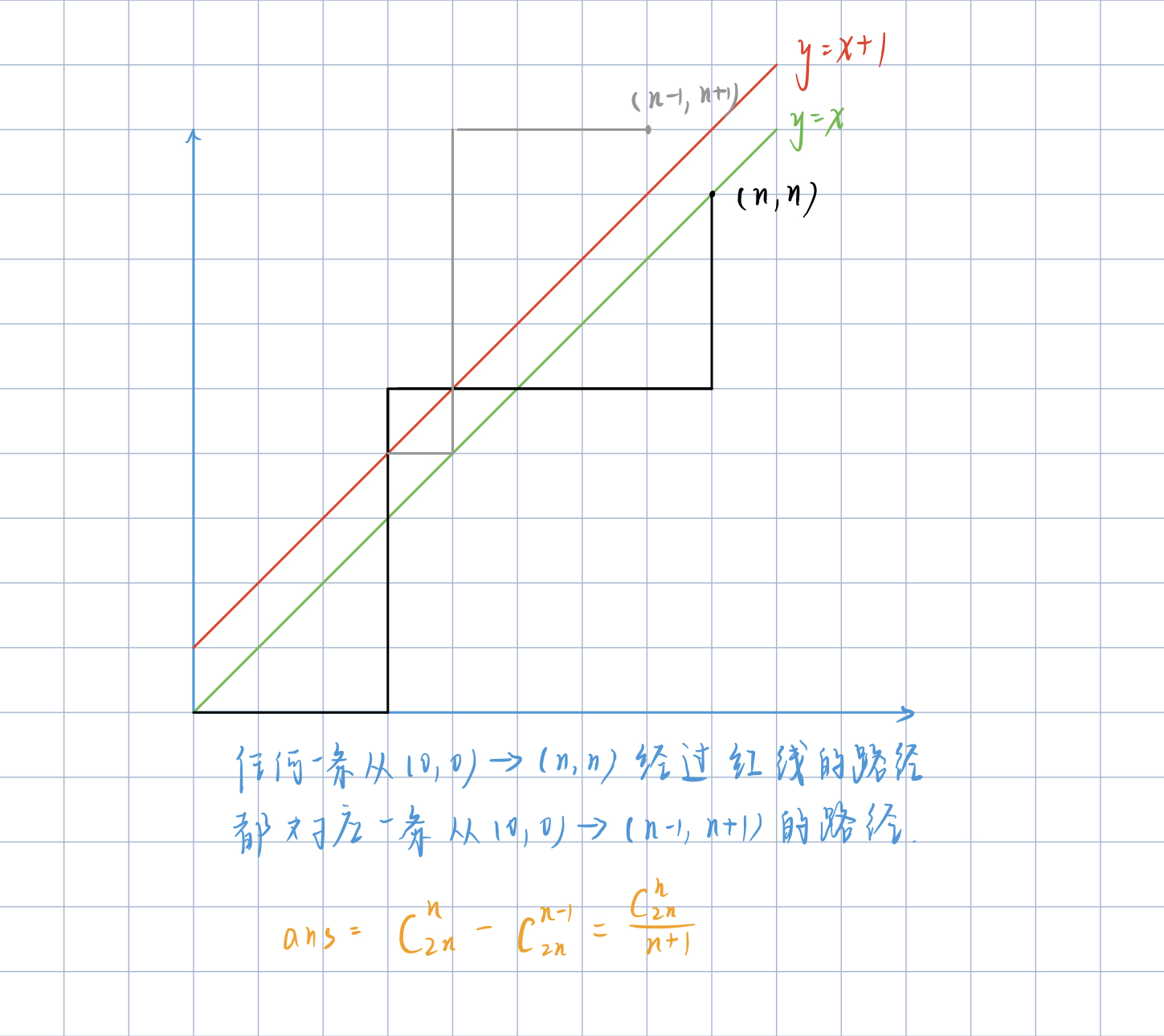
要想满足1的前缀0的数量大于1的数量就需要满足所有路过的途径在y = x这个函数个下面
但是如何表达呢？
我们采用所有到(n, n)的方案的集合减去越过y = x + 1这个直线的方案集合
因为越过y = x + 1 这个直线的方案集合可以表示为从(0, 0)到(n - 1, n + 1){(n, n)关于 y = x + 1对称的点}的方案集合
而这个答案$$C\left(\genfrac{}{}{0ex}{}{n}{2n}\right)-C\left(\genfrac{}{}{0ex}{}{n-1}{2n}\right)$$
$$=\frac{2n!}{n!\ast n!}-\frac{2n!}{(n+1)!(n-1)!}$$

$$=\frac{2n!\ast (n+1)}{n!\ast (n+1)!}-\frac{2n!\ast n}{n!\ast (n+1)!}$$

$$=\frac{1}{(n+1)}\frac{2n!}{n!\ast n!}$$
称为卡特兰数

$$=\frac{C\left(\genfrac{}{}{0ex}{}{n}{2n}\right)}{n+1}$$
2n是x的跨度和y的跨度的和

AcWing 889. 满足条件的01序列

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
int n;

int qmi(int a, int b, int c)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (LL) res * a % mod;
        a = (LL) a * a % mod;
        b >>= 1;
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    int x = 1, y = 1;
    for (int i = 1; i <= 2 * n; i ++) x = (LL)x * i % mod;
    for (int i = 1; i <= n; i ++) y = (LL)y * i % mod;
    //要注意除(n + 1) 也要求逆元因为后面还要% mod
    printf("%lld", (LL) x * qmi(y, mod - 2, mod) % mod * qmi(y, mod - 2, mod) % mod * qmi(n + 1, mod - 2, mod) % mod);
    return 0;
}