动态规划算法练习题

news2024/11/26 7:43:18

45. 跳跃游戏 II

中等

2K

相关企业

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

  • 0 <= j <= nums[i] 
  • i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1步，然后跳 3步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

  • 1 <= nums.length <= 104
  • 0 <= nums[i] <= 1000
  • 题目保证可以到达 nums[n-1]

int jump(int* nums, int numsSize){
   int *dp=(int *)malloc(sizeof(int)*numsSize);
   dp[0]=0;
   for(int i = 1 ; i < numsSize ; i++ )
    {
        dp[i] =  numsSize + 1;
    }
   for(int i =1; i< numsSize; i++)
    {
        for(int j = 0; j < i; j++)
        {
            if(j + nums[j] >= i)
            {
                dp[i] = fmin(dp[i],dp[j]+1);
            }
        }
    }
   return dp[numsSize-1];

}

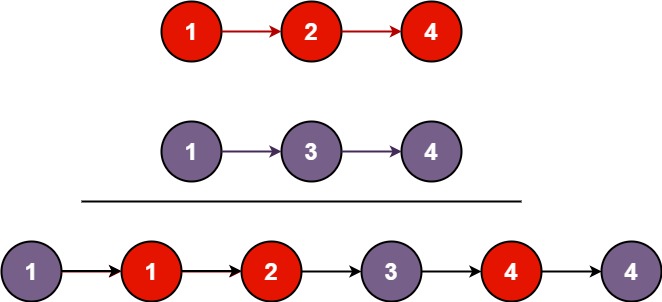
97. 交错字符串

相关企业

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

  • s = s1 + s2 + ... + sn
  • t = t1 + t2 + ... + tm
  • |n - m| <= 1
  • 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

  • 0 <= s1.length, s2.length <= 100
  • 0 <= s3.length <= 200
  • s1、s2、和 s3 都由小写英文字母组成

bool isInterleave(char * s1, char * s2, char * s3){
    int len1=strlen(s1),len2=strlen(s2),len3=strlen(s3),dp[105][105]={0};
    if(len3!=(len1+len2)){
        return false;
    }
    dp[0][0]=1;
    for(int i=0;i<=len1;i++){
        for(int j=0;j<=len2;j++){
            int p=i+j-1;
            if(i>0){
                if(dp[i-1][j]==1&&s3[p]==s1[i-1])
                    dp[i][j]=1;
            }
            if(j>0){
                 if(dp[i][j-1]==1&&s3[p]==s2[j-1])
                    dp[i][j]=1;
            }
        }
    }
    return dp[len1][len2];
}

131. 分割回文串

中等

1.4K

相关企业

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

  • 1 <= s.length <= 16
  • s 仅由小写英文字母组 
      int dp[20][20]={0};
 void dfs(char* s, int len, int begin, char*** ans, int* returnSize, int* returnColumnSizes, char** temps, int* tempsSize) {
    if(begin==len){
           char** tmp = malloc(sizeof(char*) * (*tempsSize));
        for (int j = 0; j < (*tempsSize); j++) {
            int tempsColSize = strlen(temps[j]);
            tmp[j] = malloc(sizeof(char) * (tempsColSize + 1));
            strcpy(tmp[j], temps[j]);
        }
        ans[*returnSize] = tmp;
        returnColumnSizes[(*returnSize)++] = *tempsSize;
        return;
     }
    for (int j = begin; j < len; ++j) {
        if (dp[begin][j]==1) {
            char* temp = malloc(sizeof(char) * (j - begin + 2));
                 for (int k = begin; k <= j; k++) {
                      temp[k - begin] = s[k];
                  }
            temp[j - begin + 1] = '\0';
                 temps[(*tempsSize)++]=temp;
            dfs(s, len, j + 1, ans, returnSize, returnColumnSizes, temps, tempsSize);
            --*(tempsSize);
        }
    }
}

char*** partition(char* s, int* returnSize, int** returnColumnSizes) {
     int i,j,len=strlen(s);
      int retMaxLen = len * (1 << len);
     for(i=0;i<20;i++){
         for(j=0;j<20;j++){
             dp[i][j]=0;
         }
     }
     char*** ans = malloc(sizeof(char**) * retMaxLen);
    *returnSize = 0;
    *returnColumnSizes = malloc(sizeof(int) * retMaxLen);
     for(i=len-1;i>=0;i--){
         for(j=i;j<len;j++){
             if(s[i]==s[j]){
                 if(i==j)
                    dp[i][j]=1;
                 if(j-i==1){
                     dp[i][j]=1;
                 }
                 if(j-i>1){
                     if(dp[i+1][j-1]==1){
                         dp[i][j]=1;
                     }
                 }
             }
         }
     }
      char* temps[len];
     int tempsSize=0;
    dfs(s, len, 0, ans, returnSize, *returnColumnSizes, temps, &tempsSize);
    return ans;
}

139. 单词拆分

中等

1.9K

相关企业

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
     注意，你可以重复使用字典中的单词。

示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

提示：

  • 1 <= s.length <= 300
  • 1 <= wordDict.length <= 1000
  • 1 <= wordDict[i].length <= 20
  • s 和 wordDict[i] 仅有小写英文字母组成
  • wordDict 中的所有字符串 互不相同

bool wordBreak(char * s, char ** wordDict, int wordDictSize){
   int len=strlen(s),falg=0;
   int dp[301]={0};
   dp[0]=1;
   for(int i=0;i<len;i++){
       for(int j=0;j<wordDictSize;j++){
          int n=strlen(wordDict[j]);
          if(n>(len-i)){
              continue;
          }
           falg=1;
           for(int k=0;k<n;k++){
              if(s[i+k]!=wordDict[j][k]){
                  falg=0;
                }
            }
            if(falg==1&&dp[i]==1){
                dp[i+n]=1;
            }
       }
       
   }
   if(dp[len]==1)
      return true;
   return false;
}

221. 最大正方形

中等

1.4K

相关企业

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

uploading.4e448015.gif

正在上传…重新上传取消转存失败重新上传取消

输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 300
  • matrix[i][j] 为 '0' 或 '1'

暴力超时：

int maximalSquare(char** matrix, int matrixSize, int* matrixColSize){
    int max=0;
    int m=matrixSize,n=matrixColSize[0];
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(matrix[i][j]=='1'){
                printf(" %d %d ",i,j);
                for(int b=1;i+b<=m&&j+b<=n;b++){
                    printf(" b=%d\n",b);
                    int falg=1;
                       for(int k=i;k<b+i;k++){
                           for(int l=j;l<j+b;l++){
                                if(matrix[k][l]!='1'){
                                     falg=0;
                                     break;
                                }
                            }
                       }
                       if(falg==1){
                            if(max<b)
                            {
                                max=b;
                            }
                       }
                       if(falg==0){
                           break;
                       }
                }
                
            }
        }
    }
    return max*max;
}

动态规划：

int maximalSquare(char** matrix, int matrixSize, int* matrixColSize){
    int max=0,dp[301][301]={0};
    int m=matrixSize,n=matrixColSize[0];
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(matrix[i][j]=='1'){   
               dp[i+1][j+1]=fmin(fmin(dp[i][j],dp[i][j+1]),fmin(dp[i][j],dp[i+1][j]))+1;
            }
            if(dp[i+1][j+1]>max){
                max=dp[i+1][j+1];
            }
        }
    }
    return max*max;
}

279. 完全平方数

中等

1.6K

相关企业

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

  • 1 <= n <= 104
int numSquares(int n) 
{
    int dp[n +1];   //定义dp的大小
    dp[0] = 0;      //定义dp的初始状态
    int min; 
    for(int i = 1 ; i <= n ; i++)
    {
        min = INT_MAX;
        for(int j = 1 ; j*j <= i;j++)
        {
            min = fmin(min, dp[i - j * j]);
        }
        dp[i] = min + 1;
    }
    return dp[n];
}

300. 最长递增子序列

中等

3K

相关企业

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

  • 1 <= nums.length <= 2500
  • -104 <= nums[i] <= 104

进阶：

  • 你能将算法的时间复杂度降低到 O(n log(n)) 吗?
int lengthOfLIS(int* nums, int numsSize){
    int dp[numsSize],max=0;
    for(int i=0;i<numsSize;i++){
        dp[i]=1;
        for(int j=0;j<i;j++){
            if(nums[i]>nums[j]){
                dp[i]=fmax(dp[i],dp[j]+1);
            }
        }
        if(dp[i]>max){
            max=dp[i];
        }
    }
    return max;
}

376. 摆动序列

中等

857

相关企业

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

  • 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。

  • 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000
int wiggleMaxLength(int* nums, int numsSize) {
    int up[numsSize];
    memset(up,0,sizeof(int)*numsSize);
    up[0]=1;
    int down[numsSize];
    memset(down,0,sizeof(int)*numsSize);
    down[0]=1;
    int max=0;
    for(int i=0;i<numsSize;i++){
        for(int j=0;j<i;j++){
            if(nums[i]>nums[j]){
                down[i]=fmax(up[j]+1,down[i]);
            }
            if(nums[i]<nums[j]){
                up[i]=fmax(down[j]+1,up[i]);
            }
            
        }
        if(up[i]>max){
            max=up[i];
        }
        if(down[i]>max){
            max=down[i];
        }
    }
    return max;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1332509.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

EasyExcel 导出文件的格式化

EasyExcel 导出文件的格式化

阿里开源的这个库&#xff0c;让 Excel 导出不再复杂&#xff08;既要能写&#xff0c;还要写的好看&#xff09; 之前聊了 EasyExcel 的内容导出&#xff0c;本文主要说一下导出文件的格式化&#xff0c;格式化包括工作表/单元格样式和内容格式化。毕竟&#xff0c;有时候还是…
阅读更多...
【leetcode21】合并两个有序链表Java代码讲解

【leetcode21】合并两个有序链表Java代码讲解

12.22 21. 合并两个有序链表 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1&#xff1a; 输入&#xff1a;l1 [1,2,4], l2 [1,3,4] 输出&#xff1a;[1,1,2,3,4,4]示例 2&#xff1a; 输入&#xff1a;l1 [], l2…
阅读更多...
Appium Server 启动失败常见原因及解决办法

Appium Server 启动失败常见原因及解决办法

Error: listen EADDRINUSE: address already in use 0.0.0.0:4723 如下图&#xff1a; 错误原因&#xff1a;Appium 默认的4723端口被占用 解决办法&#xff1a; 出现该提示&#xff0c;有可能是 Appium Server 已启动&#xff0c;关闭已经启动的 Appium Server 即可。472…
阅读更多...
音视频类App广告变现如何破局，最大化广告变现收益，让应用增收？

音视频类App广告变现如何破局，最大化广告变现收益，让应用增收？

音视频App已然成为了我们日常获取、发布和交换信息的重要方式&#xff0c;在音视频行业不断的拓展中&#xff0c;用户的渗透率提升。 据数据显示&#xff0c;我国网络视听用户的规模已达9亿人次&#xff0c;网民使用率也突破了90%。庞大的市场规模和用户需求吸引了大批开发者和…
阅读更多...
SRE - 监控建设

SRE - 监控建设

监控⽂档 随着信息技术的迅速发展及其在商业和工业环境中的广泛应用，系统的可靠性成为了组织的生存之本。Site Reliability Engineering（SRE）作为一种实践的结合体，广泛地用于确保和提升软件系统的可靠性。其中，它的一个重要组成部分是制定和监控服务的关键性能指标（Ser…
阅读更多...
行为型设计模式（五）：访问者模式 观察者模式

行为型设计模式（五）：访问者模式 观察者模式

访问者模式 Visitor 1、什么是访问者模式 访问者模式允许定义一些不改变数据结构的前提下的操作。通过这种方式&#xff0c;可以在不修改元素类的情况下定义新的操作。访问者模式常用于对复杂对象结构进行操作&#xff0c;而又不希望在这些对象上破坏封装性。 2、为什么使用…
阅读更多...
摄影企业网站搭建的作用是什么

摄影企业网站搭建的作用是什么

几乎每个成年人都有一部手机&#xff0c;在互联网信息时代&#xff0c;手机的作用不言而喻&#xff0c;拍照/摄像成为了不少人经常会做的事&#xff0c;拍一张美美的照片发到社交圈赢得赞声&#xff0c;或是为以后留下回忆或发给自己在意的人&#xff0c;但这只限于生活记叙类图…
阅读更多...
收集足够苹果的最小花园周长(LeetCode日记)

收集足够苹果的最小花园周长(LeetCode日记)

LeetCode-1954-收集足够苹果的最小花园周长 题目信息: 给你一个用无限二维网格表示的花园&#xff0c;每一个 整数坐标处都有一棵苹果树。整数坐标 ( i , j ) (i, j) (i,j) 处的苹果树有 ∣ i ∣ ∣ j ∣ |i| |j| ∣i∣∣j∣ 个苹果。 你将会买下正中心坐标是 ( 0 , 0 )…
阅读更多...
免费使用谷歌Gemini模型学习LLM编程

免费使用谷歌Gemini模型学习LLM编程

虽然谷歌的Gemini大语言模型爆出很大的乌龙&#xff0c;但这不影响我们使用Gemini Pro来学习LLM编程。 目前Bard还没有全部切换为Gemini Pro模型&#xff0c;但是作为程序员&#xff0c;已经不需要等待&#xff0c;可以直接调用Gemini Pro的接口了。谷歌这次开发者优先的做法值…
阅读更多...
12.23C语言 指针

12.23C语言 指针

& 地址运算符&#xff0c;用于取地址 /*注释内容*/ //注释一行 *的意思&#xff1a;1.算术运算符 2.用于指针声明int *ptr;表示这个变量是一个指针3.数组元素访问&#xff1a;在数组名后面使用 * 可以表示数组的起始地址。例如&#xff1a; int arr[5] {1, 2, 3, 4, 5…
阅读更多...
WEB 3D技术 three.js 通过lil-gui 控制x y z轴数值 操作分组 设置布尔值控制 颜色材质控制

WEB 3D技术 three.js 通过lil-gui 控制x y z轴数值 操作分组 设置布尔值控制 颜色材质控制

上文 WEB 3D技术 three.js 通过lil-gui管理公共事件中 我们用 lil-gui 处理了一下基础事件和按钮的管理 那么 本文 我们来具体说说它能做的其他事 我们先将基础代码改成这样 import ./style.css import * as THREE from "three"; //引入lil-gui import { GUI } fro…
阅读更多...
题解：CF1914E-Game with Marbles

题解：CF1914E-Game with Marbles

题解&#xff1a;CF1914E-Game with Marbles 事先说明一下&#xff0c;本题解不讲解简单数据范围的算法&#xff0c;因为复杂数据范围的就很简单。 这道题的大体意思是这样的&#xff1a;小A有颜色为i(i1~n)的小球a[i]个&#xff0c;小B有颜色为i(i1~n)的小球b[i]个。现在他们…
阅读更多...
有关List的线程安全、高效读取：不变模式下的CopyOnWriteArrayList类、数据共享通道:BlockingQueue

有关List的线程安全、高效读取：不变模式下的CopyOnWriteArrayList类、数据共享通道:BlockingQueue

有关List的线程安全 队列、链表之类的数据结构也是极常用的&#xff0c;几乎所有的应用程序都会与之相关。在java中&#xff0c; ArrayList和Vector都使用数组作为其内部实现。两者最大的不同在与Vector是线程安全的。 而ArrayList不是。此外LinkedList使用链表的数据结构实现…
阅读更多...
ubuntu 22.04 安装mysql服务

ubuntu 22.04 安装mysql服务

完整内容&#xff1a; https://developer.aliyun.com/article/1260321 # 安装服务 sudo apt install mysql-server# 按向导设置root密码 sudo mysql_secure_installation# 使用设置的密码登录 sudo mysql -u root -p也可以使用工具登录&#xff0c;例如: navicat for mysql
阅读更多...
掌握iText：轻松实现固定pdf模板的动态数据填充

掌握iText：轻松实现固定pdf模板的动态数据填充

推荐语 如果你在工作中需要处理大量的PDF表单&#xff0c;那么使用iText5实现固定PDF模板的动态数据填充&#xff0c;将是一种非常有效的方法。这篇技术文章详细介绍了如何使用iText5库来读取已有的PDF模板&#xff0c;并动态地填充表单数据&#xff0c;生成最终的表单文件。通…
阅读更多...
虚拟机的下载、安装(模拟出服务器)

虚拟机的下载、安装(模拟出服务器)

下载 vmware workstation&#xff08;收费的虚拟机&#xff09; 下载vbox 网址&#xff1a;Oracle VM VirtualBox&#xff08;免费的虚拟机&#xff09; 以下选择一个下载即可&#xff0c;建议下载vbox&#xff0c;因为是免费的。安装的时候默认下一步即可&#xff08;路径最好…
阅读更多...
Vue2从源码角度来回答一些常见的问题

Vue2从源码角度来回答一些常见的问题

1.请说一下Vue2响应式数据的理解&#xff08;先知道基本的问题在哪里&#xff0c;源码的角度来回答&#xff0c;用的时候会有哪些问题&#xff09; 可以监控一个数据的修改和获取操作。针对对象格式会给每个对象的属性进行劫持 Object.defineProperty 源码层面 initData ->…
阅读更多...
卷积神经网络基础与补充

卷积神经网络基础与补充

参考自 up主的b站链接&#xff1a;霹雳吧啦Wz的个人空间-霹雳吧啦Wz个人主页-哔哩哔哩视频这位大佬的博客 https://blog.csdn.net/m0_37867091?typeblog CNN的历史发展&#xff1a; 这一点老师上课的时候也有讲到&#xff0c;BP的出现对CNN的发展至关重要 卷积的特性&#x…
阅读更多...
nodejs+vue+ElementUi大学新生入学系统的设计与实现1hme0

nodejs+vue+ElementUi大学新生入学系统的设计与实现1hme0

采用B/S模式架构系统&#xff0c;开发简单&#xff0c;只需要连接网络即可登录本系统&#xff0c;不需要安装任何客户端。开发工具采用VSCode&#xff0c;前端采用VueElementUI&#xff0c;后端采用Node.js&#xff0c;数据库采用MySQL。 涉及的技术栈 1&#xff09; 前台页面…
阅读更多...
kubelet源码学习（二）：kubelet创建Pod流程

kubelet源码学习（二）：kubelet创建Pod流程

本文基于Kubernetes v1.22.4版本进行源码学习 4、kubelet创建Pod流程 syncLoop()的主要逻辑是在syncLoopIteration()方法中实现&#xff0c;Pod创建相关代码只需要看处理configCh部分的代码 // pkg/kubelet/kubelet.go // 该方法会监听多个channel,当发现任何一个channel有数…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023