非线性约束的优化问题_序列二次规划算法代码

news2025/1/16 20:12:01

1. 理论部分

2. 序列二次规划算法代码及解析

3.完整代码

1.理论部分

a.约束优化问题的极值条件

库恩塔克条件(Kuhn-Tucker conditions，KT条件)是确定某点为极值点的必要条件。如果所讨论的规划是凸规划，那么库恩-塔克条件也是充分条件。

（1）判断数值x处起作用的约束，计算x处各约束的取值是否为0，找出起作用的约束条件。并非所有约束条件都起作用，即并非落在所有约束条件的边界交集处。对于起作用的边界条件，满足边界函数g(x)或h(x)为0；

（2）数值x处，目标函数导数f'(x)和起作用的约束导数g'(x)的数值；

（3）代入KT条件（ex. f'(x) + \lambda_1 g'(x_1) + \lambda_2 g'(x_2) =0），求解拉格朗日乘子λ的大小，判断λ是否大于0，若大于零，则为极值点。

（4）若不满足条件，继续迭代。

具体做法如下：

其中λ为拉格朗日乘子，当某一点x使λ > 0存在时，称满足KT条件，则该点x是极值点。
约束优化问题的应用示例如下图：

b.约束优化方法及迭代
此处介绍和使用外惩罚函数法/外点法

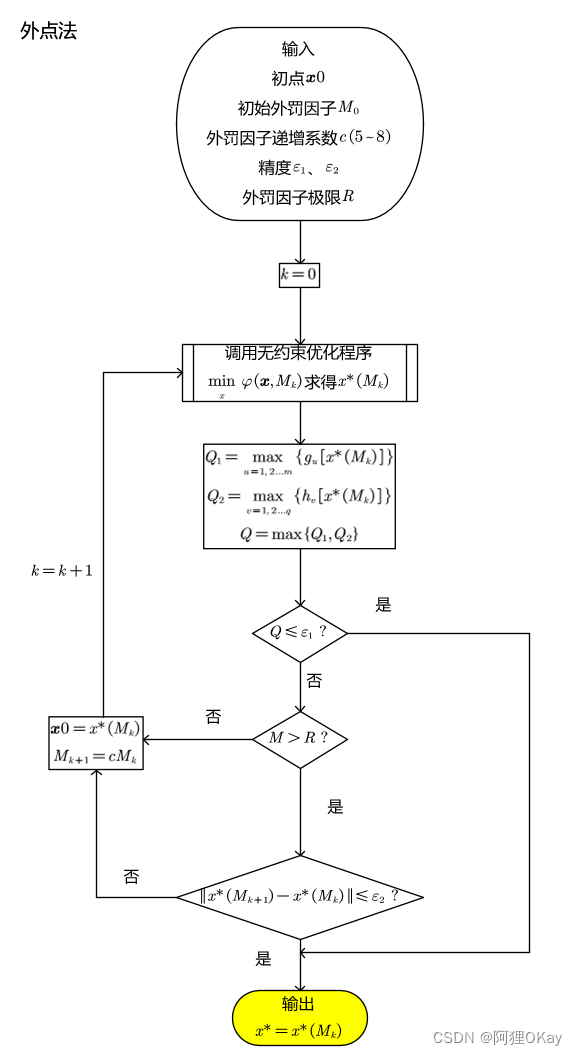
外点法是一种从随机一点（一般在可行域外）出发，逐渐移动到可行区域的方法。
对于约束优化问题：

\min_{x}f(x)

s.t. \space g_u(x) \leqslant 0, \space u=1,2,...m

s.t. \space h_v(x) = 0, \space v=1,2,...p

构造外惩罚函数：

\Phi(x, M_k) = f(x) + M_k \left \{ \sum_{u=1}^{m} (max[g_u(x),0])^2 + \sum_{v=1}^{p} (h_v(x))^2 \right \}

即，当g(x)不满足条件时，该项有大于0的值，h(x)不满足条件时，该项也有值，加和的越大代表该数值点距离距离约束的可行域越远，惩罚项的值越大，惩罚作用越明显。。其中Mk为外罚因子，M 0 < M 1 < M 2 . . . < M k 为递增的正数序列，一般M0=1，递增系数c=5~8。

迭代终止满足两个判断条件中一个即可：

1. Q\leqslant 10^{-3}，Q为当前数值点多个约束函数中最大的值，即满足了所有的约束函数条件。

2. M> R 且 \left \| xM_{k+1} - xM_k \right \| \leqslant \epsilon，R为外罚因子控制量，M超出外罚因子的极限R

外点法的迭代图如下：

外点法的示例如下图：

a. 定义变量

vars = 2; % 自变量数量
cons = 1; % 约束数量
maxIter=100; % 最大迭代次数
x = [-1;4]; % 初始猜测值
l =0; % 拉格朗日乘子
H = eye(vars,vars); % Hessian 矩阵，假设为I矩阵

目标函数为

f(x)= x_1^4 - 2x_1^2x_2+x_2^2+x_1^2-2x_1+5

及目标函数的导数为

f'(x_1) = 4x_1^3 - 4x_1x_2 + 2x_1 - 2

f'(x_2) = -2x_1^2 + 2x_2

function y = f(x)
    y = x(1)^4 - 2*x(2)*x(1)^2 + x(2)^2 + x(1)^2 - 2*x(1)+5;
end

function y = gradf(x)
    y(1) = 2*x(1)-4*x(1)*x(2)+4*x(1)^3-2;
    y(2) = -2*x(1)^2 + 2*x(2);
end

约束项不等式为

-(x_1 + 0.25)^2 + 0.75x_2 >= 0

以及其导数为

g'(x_1) = -2(x_1 -0.25)=-2x_1-0.5

g'(x_2) = 0.75

function y = g(x)
    y(1) = -(x(1)+0.25)^2+0.75*x(2);
end

function y = gradg(x)
    y(1,1) = -2*x(1)-1/2;
    y(1,2) = 3/4;
end

求解KKT条件

function y = SolveKKT(gradfEval,gradgEval,gEval,Hessian)
    A = [Hessian -gradgEval';gradgEval 0]; %对称矩阵，约束函数的梯度矩阵
    b = [-gradfEval -gEval]';
    y = A\b; %方程  Ay = b 解出y值，分别对应最优的x值的梯度和最优的拉格朗日乘子的值
    %即此时Ay-b = 0，kkt条件成立，
end

判断数值点x是否满足约束条件

function [gViol,lViol] = Viols(gEval,l)%约束条件函数值，拉格朗日乘子l
    gViol=[];
    lViol=[];
    for i = 1:length(gEval)
        if gEval(i)<0  %如果约束条件函数值小于零，即，不满足约束条件
            gViol(i)=gEval(i); %将约束条件函数值和拉格朗日乘子l，放入列表
            lViol(i)=l(i);
        end    
    end
end

处理不满足约束的情况，构造惩罚函数，lViol对应Mk，累加得到惩罚函数

function y = Penalty(fEval,gViol,lViol)
%代入该点处的函数值，不满足约束的约束函数值，以及拉格朗日乘子l
    sum = 0;
    y = fEval;
    for i = 1:length(gViol) %找出不满足约束条件的约束函数值
        sum = sum +  lViol(i)*abs(gViol(i)); %约束函数值g(x)求反，再乘一个系数，即，||l_1*g(x1)+l2*g(x2) ||
    end
    y = y + sum;
end

在初始点首先进行初始计算，找出不满足约束的约束，计算其损失函数。

% EVALUATE AT STARTING POINT

fEval= f(x);
gEval = g(x);
[gViol,lViol] = Viols(gEval,l); 
gradfEval = gradf(x);
gradgEval = gradg(x);
P = Penalty(fEval,gViol,lViol);

开始进入SQP算法主体,求解kkt条件，得到xSol为函数x的解，lSol为拉格朗日乘子的解。

for i=1:maxIter %开始循环迭代

    % SOLVE KKT CONDITIONS FOR THE OPTIMUM OF THE QUADRATIC APPROXIMATION
    %求解二次优化的KKT条件
    sol = SolveKKT(gradfEval,gradgEval,gEval,H);%代入导数f'(x)，g'(x),约束函数值g(x)，Hessian矩阵，
    xSol = sol(1:vars);
    lSol = sol(vars+1:vars+cons);

如果拉格朗日乘子有负的，即，不满足约束条件，则将其设为0，并重新求解方程\frac{\partial {f_(x^*)}^2 }{\partial x^2} {sol}= f'(x^*)

    for j = 1:length(lSol)
        if lSol(j)<0    %如果拉格朗日乘子有一个是负的
            sol= H\(-gradfEval)'; %将结果重新求解H*x = -gradfEval
            xSol = sol(1:vars);
            lSol(j)=0;  %该约束的拉格朗日乘子置为0
        end
    end

计算新的数值点情况

    xNew = x + xSol; %更新得到新的数值点
    lNew = lSol;  % 得到新的拉格朗日乘子
    fEvalNew = f(xNew);%计算新点目标函数的数值
    gEvalNew = g(xNew);%计算新点的约束函数数值
    gradfEvalNew = gradf(xNew);%计算该点目标函数梯度
    gradgEvalNew = gradg(xNew);%计算该点约束函数梯度
    [gViolNew,lViolNew] = Viols(gEvalNew,lNew);%找出不满足的约束条件
    PNew = Penalty(fEvalNew,gViolNew,lViolNew);%求解惩罚函数

如果惩罚函数增加，减小步长到原来的一半

    % IF PENALTY FUNCTION INCREASED, LOWER THE STEP BY 0.5
    
    while PNew-P>1e-4
        xSol = 0.5*xSol;
        xNew = x + xSol;
        fEvalNew = f(xNew);
        gEvalNew = g(xNew);
        gradfEvalNew = gradf(xNew);
        gradgEvalNew = gradg(xNew);
        [gViolNew,lViolNew] = Viols(gEvalNew,lNew);
        PNew = Penalty(fEvalNew,gViolNew,lViolNew);
    end

如果x数值变化很小，停止迭代，找到最优，结束迭代

    % STOPPING CRITERION
    
    if norm(xNew(1:vars)-x(1:vars))<=1e-2
        break
    end

更新Hessian矩阵，Q为Mk+1- Mk的值

    % UPDATE THE HESSIAN
    
    gradLEval = gradLagr(gradfEval,gradgEval,lNew,vars); 
    %拉格朗日函数的梯度 lnew not l!!!
    gradLEvalNew = gradLagr(gradfEvalNew,gradgEvalNew,lNew,vars);
    %新的数值点处，拉格朗日函数的梯度
    Q = gradLEvalNew-gradLEval;
    %拉格朗日函数数值的差分L(x_k+1) - L(x_k)
    dx = xNew-x;
    %自变量x的差分
    HNew = UpdateH(H,dx,Q);%求解H矩阵

计算拉格朗日乘子梯度的函数

function y = gradLagr(gradfEval,gradgEval,l,n)
    y = gradfEval';
    sum = zeros(n,1);
        for i = 1:length(l)
            sum = sum -l(i)*gradgEval(i:n)';
        end
    y = y + sum;  %x处目标函数的梯度，减去约束函数的梯度。即，拉格朗日函数的梯度
end

更新Hessian矩阵，gamma为Mk+1- Mk的值

function y = UpdateH(H,dx,gamma)%gamma是拉格朗日函数的两次差分
    term1=(gamma*gamma') / (gamma'*dx);
    term2 = ((H*dx)*(dx'*H)) / (dx'*(H*dx));
    y = H + term1-term2; %更新得到新的H矩阵
end

更新所有的变量，用于下次的迭代，包括Hessian矩阵H，数值点x，惩罚函数值P，目标函数值fEval，目标函数值梯度gradEval，约束函数值gEval，约束函数值梯度gradgEval

    % UPDATE ALL VALUES FOR NEXT ITERATION
    
    H = HNew;
    fEval = fEvalNew;
    gEval = gEvalNew;
    gradfEval = gradfEvalNew;
    gradgEval = gradgEvalNew;
    P = PNew;
    x = xNew;

3.可以运行的完整代码如下：

% EXAMPLE OF SQP ALGORITHM

clear variables; close all; clc;
fprintf("---------------------------------------------------------------\n")
fprintf("An implementation of Sequential Quadratic Programming method\nin a nonlinear constrained optimization problem\n")
fprintf("---------------------------------------------------------------\n")

% INITIAL VALUES - INPUT

vars = 2; % number of variables
cons = 1; % number of constraints
maxIter=100; % max iterations
x = [-1;4]; % initial guess point
l =0; % LagrangeMultipliers vector
H = eye(vars,vars); % Hessian matrix assumed to be identity

% EVALUATE AT STARTING POINT

fEval= f(x);
gEval = g(x);
[gViol,lViol] = Viols(gEval,l); 
gradfEval = gradf(x);
gradgEval = gradg(x);
P = Penalty(fEval,gViol,lViol);

% SQP ALGORITHM

for i=1:maxIter

    % SOLVE KKT CONDITIONS FOR THE OPTIMUM OF THE QUADRATIC APPROXIMATION
    
    sol = SolveKKT(gradfEval,gradgEval,gEval,H);
    xSol = sol(1:vars);
    lSol = sol(vars+1:vars+cons);
    
    % IF THE LAGRANGE MULTIPLIER IS NEGATIVE SET IT TO ZERO
    
    for j = 1:length(lSol)
        if lSol(j)<0 
            sol= H\(-gradfEval)';
            xSol = sol(1:vars);
            lSol(j)=0;
        end
    end
    
    % EVALUATE AT NEW CANDIDATE POINT
    
    xNew = x + xSol; 
    lNew = lSol;
    fEvalNew = f(xNew);
    gEvalNew = g(xNew);
    gradfEvalNew = gradf(xNew);
    gradgEvalNew = gradg(xNew);
    [gViolNew,lViolNew] = Viols(gEvalNew,lNew);
    PNew = Penalty(fEvalNew,gViolNew,lViolNew);
    
    % IF PENALTY FUNCTION INCREASED, LOWER THE STEP BY 0.5
    
    while PNew-P>1e-4
        xSol = 0.5*xSol;
        xNew = x + xSol;
        fEvalNew = f(xNew);
        gEvalNew = g(xNew);
        gradfEvalNew = gradf(xNew);
        gradgEvalNew = gradg(xNew);
        [gViolNew,lViolNew] = Viols(gEvalNew,lNew);
        PNew = Penalty(fEvalNew,gViolNew,lViolNew);
    end
    
    % STOPPING CRITERION
    
    if norm(xNew(1:vars)-x(1:vars))<=1e-2
        break
    end
    
    % UPDATE THE HESSIAN
    
    gradLEval = gradLagr(gradfEval,gradgEval,lNew,vars); % lnew not l!!!
    gradLEvalNew = gradLagr(gradfEvalNew,gradgEvalNew,lNew,vars);
    Q = gradLEvalNew-gradLEval;
    dx = xNew-x;
    HNew = UpdateH(H,dx,Q);
    
    % UPDATE ALL VALUES FOR NEXT ITERATION
    
    H = HNew;
    fEval = fEvalNew;
    gEval = gEvalNew;
    gradfEval = gradfEvalNew;
    gradgEval = gradgEvalNew;
    P = PNew;
    x = xNew;
end

fprintf('SQP: Optimum point:\n x1=%10.4f\n x2=%10.4f\n iterations =%10.0f \n', x(1), x(2), i)

% FUNCTIONS NEEDED

function y = SolveKKT(gradfEval,gradgEval,gEval,Hessian)
    A = [Hessian -gradgEval';gradgEval 0];
    b = [-gradfEval -gEval]';
    y = A\b;
end

function y = f(x)
    y = x(1)^4 - 2*x(2)*x(1)^2 + x(2)^2 + x(1)^2 - 2*x(1)+5;
end

function y = gradf(x)
    y(1) = 2*x(1)-4*x(1)*x(2)+4*x(1)^3-2;
    y(2) = -2*x(1)^2 + 2*x(2);
end

function y = gradLagr(gradfEval,gradgEval,l,n)
    y = gradfEval';
    sum = zeros(n,1);
        for i = 1:length(l)
            sum = sum -l(i)*gradgEval(i:n)';
        end
    y = y + sum;
end


function y = gradg(x)
    y(1,1) = -2*x(1)-1/2;
    y(1,2) = 3/4;
end

function y = g(x)
    y(1) = -(x(1)+0.25)^2+0.75*x(2);
end

function [gViol,lViol] = Viols(gEval,l)
    gViol=[];
    lViol=[];
    for i = 1:length(gEval)
        if gEval(i)<0
            gViol(i)=gEval(i);
            lViol(i)=l(i);
        end    
    end
end


function y = Penalty(fEval,gViol,lViol)
    sum = 0;
    y = fEval;
    for i = 1:length(gViol)
        sum = sum +  lViol(i)*abs(gViol(i));
    end
    y = y + sum;
end

function y = UpdateH(H,dx,gamma)
    term1=(gamma*gamma') / (gamma'*dx);
    term2 = ((H*dx)*(dx'*H)) / (dx'*(H*dx));
    y = H + term1-term2;
end

最后输出结果为：

---------------------------------------------------------------
An implementation of Sequential Quadratic Programming method
in a nonlinear constrained optimization problem
---------------------------------------------------------------
SQP: Optimum point:
 x1=    0.4999
 x2=    0.7498
 iterations =         9

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1331525.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JBoss JMXInvokerServlet 反序列化漏洞 CVE-2015-7501 已亲自复现

JBoss JMXInvokerServlet 反序列化漏洞 CVE-2015-7501 已亲自复现

JBoss JMXInvokerServlet 反序列化漏洞 CVE-2015-7501 已亲自复现 漏洞名称漏洞描述影响版本 漏洞复现环境搭建漏洞利用 修复建议总结 漏洞名称 漏洞描述 在Oracle Rapid Planning 12.1/12.2.2中发现了一个被归类为“严重”的漏洞。受到影响的是一些未知的组件处理中间层。升…
阅读更多...
SQL进阶理论篇（二十）：什么是SQL注入

SQL进阶理论篇（二十）：什么是SQL注入

文章目录 简介SQL注入的原理SQL注入的实例搭建sqli-labs注入环境实例一&#xff1a;猜测where条件判断查询语句的字段数获取当前数据库和用户信息获取MySQL中的所有数据库名称查询wucai数据库中的所有数据表查询heros数据表中的所有字段参考文献 简介 这节是纯兴趣篇了。 web…
阅读更多...
RocketMQ事务消息实现分布式事务

RocketMQ事务消息实现分布式事务

文章目录 简介实现原理实现逻辑 简介 RocketMQ事务消息 RocketMQ在4.3.0版中支持分布式事务消息&#xff0c;这里RocketMQ的事务消息是采用2PC(两段式协议) 补偿机制&#xff08;消息回查&#xff09;的分布式事务功能。提供消息发送与业务落库的一致性。 RocketMQ事务消息&am…
阅读更多...
MicroPython的交互式解释器模式 REPL

MicroPython的交互式解释器模式 REPL

MicroPython的交互式解释器模式又名REPL&#xff08;read-eval-print-loop&#xff09;&#xff0c;就是一种命令输入交互模式&#xff0c;跟Python的REPL是类似的&#xff0c;就是在命令行直接输入Python代码或表达式执行并打印结果。关于MicroPython的REPL跟通常的Python类似…
阅读更多...
电子病历编辑器源码，提供电子病历在线制作、管理和使用的一体化电子病历解决方案

电子病历编辑器源码，提供电子病历在线制作、管理和使用的一体化电子病历解决方案

概述&#xff1a; 电子病历是指医务人员在医疗活动过程中,使用医疗机构信息系统生成的文字、符号、图表、图形、数据、影像等数字化信息,并能实现存储、管理、传输和重现的医疗记录,是病历的一种记录形式。 医院通过电子病历以电子化方式记录患者就诊的信息&#xff0c;包括&…
阅读更多...
【常见的语法糖（详解）】

【常见的语法糖（详解）】

&#x1f7e9; 说几个常见的语法糖 &#x1f7e2;关于语法糖的典型解析&#x1f7e2;如何解语法糖&#xff1f;&#x1f7e2;糖块一、switch 支持 String 与枚举&#x1f4d9;糖块二、泛型&#x1f4dd;糖块三、自动装箱与拆箱&#x1f341;糖块四、方法变长参数&#x1f5a5;️…
阅读更多...
Linux多线程：POSIX信号量，基于信号量的环形队列实现生产者消费者模型

Linux多线程：POSIX信号量，基于信号量的环形队列实现生产者消费者模型

目录 一、POSIX信号量1.1 初始化信号量1.2 销毁信号量1.3 等待信号量1.4 发布信号量1.5 基于环形队列的生产消费模型(用信号量控制生产者和消费者之间的同步互斥关系)1.5.1 makefile1.5.2 RingQueue.hpp1.5.3 Sem.hpp1.5.4 Task.hpp1.5.5 main.cc 二、信号量控制的环形队列原理…
阅读更多...
.Net 访问电子邮箱-LumiSoft.Net，好用

.Net 访问电子邮箱-LumiSoft.Net，好用

序言&#xff1a; 网上找了很多关于.Net如何访问电子邮箱的方法&#xff0c;但是大多数都达不到想要的需求&#xff0c;只有一些 收发邮件。因此 花了很大功夫去看 LumiSoft.Net.dll 的源码&#xff0c;总算做出自己想要的结果了&#xff0c;果然学习诗人进步。 介绍&#xff…
阅读更多...
Qt 开源项目

Qt 开源项目

Qt 开源项目 Omniverse View链接技术介绍 QuickQanava链接技术介绍QField链接技术介绍 AtomicDEX链接技术介绍 Status-desktop链接技术介绍 Librum链接技术介绍 A Simple Cross-Platform ReaderQPrompt链接技术介绍 GCompris链接技术介绍 Scrite链接技术介绍 QSkinny链接技术介…
阅读更多...
如何在PC上运行大模型

如何在PC上运行大模型

如何在PC上运行大模型 在PC上使用CPU运行大模型不如使用GPU高效&#xff0c;但仍然是可以实现的大模型推理。 大模型训练要求的资源更高&#xff0c;这里直接使用面向开源的Facebook’s LLaMA model(llama-2-7b-chat.Q2_K.gguf)。 连接CPU与LLaMA model的是llama.cpp。 为方便…
阅读更多...
认识Linux背景

认识Linux背景

1.发展史 Linux从哪里来&#xff1f;它是怎么发展的&#xff1f;在这里简要介绍Linux的发展史 要说Linux&#xff0c;还得从UNIX说起 UNIX发展的历史 1968年&#xff0c;一些来自通用电器公司、贝尔实验室和麻省理工学院的研究人员开发了一个名叫Multics的特殊操作系统。Mu…
阅读更多...
LLaMA开源大模型源码分析！

LLaMA开源大模型源码分析！

Datawhale干货 作者&#xff1a;宋志学&#xff0c;Datawhale成员 花了一晚上照着transformers仓库的LLaMA源码&#xff0c;把张量并行和梯度保存的代码删掉&#xff0c;只留下模型基础结构&#xff0c;梳理了一遍LLaMA的模型结构。 今年四月份的时候&#xff0c;我第一次接触…
阅读更多...
第一次记录QPSK，BSPK，MPSK，QAM—MATLAB实现

第一次记录QPSK，BSPK，MPSK，QAM—MATLAB实现

最近有偶然的机会学习了一次QPSK防止以后忘记又得找资料&#xff0c;这里就详细的记录一下 基于 QPSK 的通信系统如图 1 所示&#xff0c;QPSK 调制是目前最常用的一种卫星数字和数 字集群信号调制方式&#xff0c;它具有较高的频谱利用率、较强的抗干扰性、在电路上实现也较为…
阅读更多...
基于STM32单片机模拟智能电梯步进电机控制升降毕业设计3

基于STM32单片机模拟智能电梯步进电机控制升降毕业设计3

STM32单片机模拟智能电梯步进电机控制数码管显示3 演示视频&#xff08;复制到浏览器打开&#xff09;&#xff1a; 基于STM32单片机的智能电梯控制系统模拟智能电梯步进电机控制系统设计数码管显示楼层设计/DIY开发板套件3 产品功能描述&#xff1a; 本系统由STM32F103C8T6单…
阅读更多...
技术交底二维码的应用

技术交底二维码的应用

二维码技术交底可以逐级落实、责任到人、有据可查、是目前最方便、实用的交底方式&#xff0c;下面我们讲解技术交底二维码的应用。 1、生成对应的技术交底二维码&#xff0c;将施工方案、技术资料、安全教育资料等内容上传到二维码里。打印出来现场粘贴&#xff0c;便于作业班…
阅读更多...
（一）深入理解Mysql底层数据结构和算法

（一）深入理解Mysql底层数据结构和算法

什么是索引 索引是帮助MySQL高效获取数据的排好序的数据结构 数据结构有哪些 数据结构模拟网站&#xff1a;Data Structure Visualization 二叉树 不适合做自增ID的数据结构。如下示意图&#xff0c;假设采用二叉树作为表自增主键ID的数据存储结果如下&#xff1a;当查询i…
阅读更多...
行列式：方程组未知数的计算：克拉默法则

行列式：方程组未知数的计算：克拉默法则

行列式&#xff1a;方程组未知数的计算 ![ ](https://img-blog.csdnimg.cn/direct/4a9c2800da3746ea95c1a3c93057d796.png)
阅读更多...
VS Code实现“Ctr+save”保存代码自动格式化

VS Code实现“Ctr+save”保存代码自动格式化

一、下载Prettier - Code formatter插件 点击安装即可 二、配置 【1】打开文件——首选项——设置 或者左下角齿轮打开设置 【2】搜索设置框输入editor default formatter&#xff08;意思是默认格式化设置&#xff09;&#xff0c;接着下拉选中刚下好的插件名称Prettier - C…
阅读更多...
【Vulnhub 靶场】【Corrosion: 1】【简单】【20210731】

【Vulnhub 靶场】【Corrosion: 1】【简单】【20210731】

1、环境介绍 靶场介绍&#xff1a;https://www.vulnhub.com/entry/corrosion-1,730/ 靶场下载&#xff1a;https://download.vulnhub.com/corrosion/Corrosion.ova 靶场难度&#xff1a;简单 发布日期&#xff1a;2021年07月31日 文件大小&#xff1a;7.8 GB 靶场作者&#xf…
阅读更多...
Windows安装cnpm报错 The operation was rejected by your operating system.

Windows安装cnpm报错 The operation was rejected by your operating system.

Windows在安装cnpm时出现如下错误 npm ERR! The operation was rejected by your operating system. npm ERR! Its possible that the file was already in use (by a text editor or antivirus), npm ERR! or that you lack permissions to access it. npm ERR! npm ERR! If y…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023