一、题目
字典wordList中从单词beginWord和endWord的 转换序列 是一个按下述规格形成的序列beginWord -> s1 -> s2 -> ... -> sk:
1、每一对相邻的单词只差一个字母。
2、对于1 <= i <= k时,每个si都在wordList中。注意,beginWord不需要在wordList中。
3、sk == endWord
给你两个单词beginWord和endWord和一个字典wordList,返回从beginWord到endWord的最短转换序列中的单词数目 。如果不存在这样的转换序列,返回0。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是hit->hot-> dot -> dog -> cog, 返回它的长度5。
示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord cog不在字典中,所以无法进行转换。
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord和wordList[i]由小写英文字母组成
beginWord != endWord
wordList中的所有字符串 互不相同
二、代码
【1】广度优先搜索 + 优化建图: 本题要求的是最短转换序列的长度,看到最短首先想到的就是广度优先搜索。想到广度优先搜索自然而然的就能想到图,但是本题并没有直截了当的给出图的模型,因此我们需要把它抽象成图的模型。我们可以把每个单词都抽象为一个点,如果两个单词可以只改变一个字母进行转换,那么说明他们之间有一条双向边。因此我们只需要把满足转换条件的点相连,就形成了一张图。
基于该图,我们以beginWord为图的起点,以endWord为终点进行广度优先搜索,寻找beginWord到endWord的最短路径。
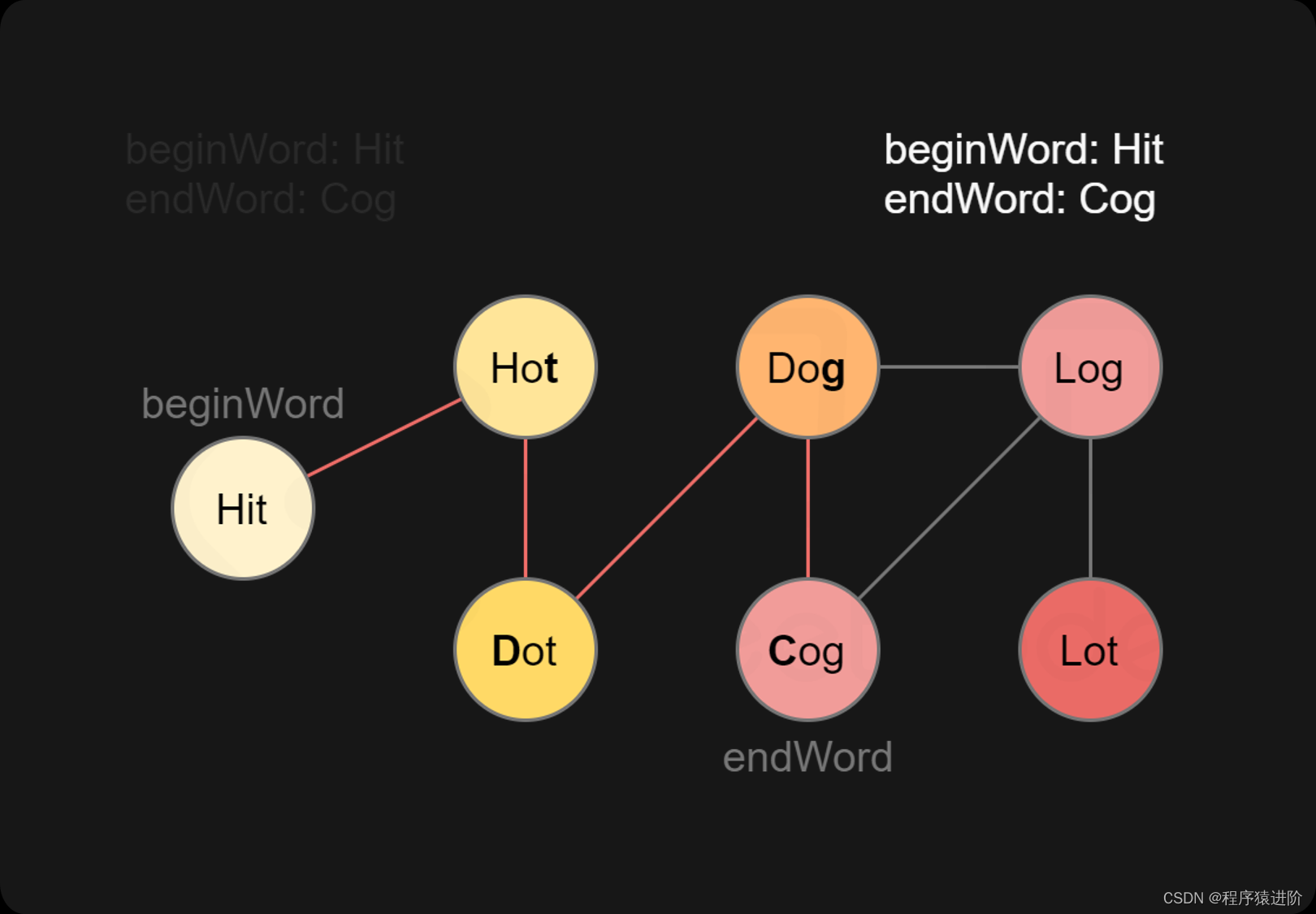
基于上面的思路我们考虑如何编程实现。首先为了方便表示,我们先给每一个单词标号,即给每个单词分配一个id。创建一个由单词word到id对应的映射wordId,并将beginWord与wordList中所有的单词都加入这个映射中。之后我们检查endWord是否在该映射内,若不存在,则输入无解。我们可以使用哈希表实现上面的映射关系。
然后我们需要建图,依据朴素的思路,我们可以枚举每一对单词的组合,判断它们是否恰好相差一个字符,以判断这两个单词对应的节点是否能够相连。但是这样效率太低,我们可以优化建图。具体地,我们可以创建虚拟节点。对于单词hit,我们创建三个虚拟节点*it、h*t、hi*,并让hit向这三个虚拟节点分别连一条边即可。如果一个单词能够转化为hit,那么该单词必然会连接到这三个虚拟节点之一。对于每一个单词,我们枚举它连接到的虚拟节点,把该单词对应的id与这些虚拟节点对应的id相连即可。
最后我们将起点加入队列开始广度优先搜索,当搜索到终点时,我们就找到了最短路径的长度。注意因为添加了虚拟节点,所以我们得到的距离为实际最短路径长度的两倍。同时我们并未计算起点对答案的贡献,所以我们应当返回距离的一半再加一的结果。
class Solution {
Map<String, Integer> wordId = new HashMap<String, Integer>();
List<List<Integer>> edge = new ArrayList<List<Integer>>();
int nodeNum = 0;
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
for (String word : wordList) {
addEdge(word);
}
addEdge(beginWord);
if (!wordId.containsKey(endWord)) {
return 0;
}
int[] dis = new int[nodeNum];
Arrays.fill(dis, Integer.MAX_VALUE);
int beginId = wordId.get(beginWord), endId = wordId.get(endWord);
dis[beginId] = 0;
Queue<Integer> que = new LinkedList<Integer>();
que.offer(beginId);
while (!que.isEmpty()) {
int x = que.poll();
if (x == endId) {
return dis[endId] / 2 + 1;
}
for (int it : edge.get(x)) {
if (dis[it] == Integer.MAX_VALUE) {
dis[it] = dis[x] + 1;
que.offer(it);
}
}
}
return 0;
}
public void addEdge(String word) {
addWord(word);
int id1 = wordId.get(word);
char[] array = word.toCharArray();
int length = array.length;
for (int i = 0; i < length; ++i) {
char tmp = array[i];
array[i] = '*';
String newWord = new String(array);
addWord(newWord);
int id2 = wordId.get(newWord);
edge.get(id1).add(id2);
edge.get(id2).add(id1);
array[i] = tmp;
}
}
public void addWord(String word) {
if (!wordId.containsKey(word)) {
wordId.put(word, nodeNum++);
edge.add(new ArrayList<Integer>());
}
}
}
时间复杂度: O(N×C^2)。其中N为wordList的长度,C为列表中单词的长度。
1、建图过程中,对于每一个单词,我们需要枚举它连接到的所有虚拟节点,时间复杂度为O(C),将这些单词加入到哈希表中,时间复杂度为O(N×C),因此总时间复杂度为O(N×C)。
2、广度优先搜索的时间复杂度最坏情况下是O(N×C)。每一个单词需要拓展出O(C)个虚拟节点,因此节点数O(N×C)。
空间复杂度: O(N×C^2)。其中N为wordList的长度,C为列表中单词的长度。哈希表中包含O(N×C)个节点,每个节点占用空间O(C),因此总的空间复杂度为O(N×C^2)。
双向广度优先搜索: 根据给定字典构造的图可能会很大,而广度优先搜索的搜索空间大小依赖于每层节点的分支数量。假如每个节点的分支数量相同,搜索空间会随着层数的增长指数级的增加。考虑一个简单的二叉树,每一层都是满二叉树的扩展,节点的数量会以2为底数呈指数增长。如果使用两个同时进行的广搜可以有效地减少搜索空间。一边从beginWord开始,另一边从endWord开始。我们每次从两边各扩展一层节点,当发现某一时刻两边都访问过同一顶点时就停止搜索。这就是双向广度优先搜索,它可以可观地减少搜索空间大小,从而提高代码运行效率。
class Solution {
Map<String, Integer> wordId = new HashMap<String, Integer>();
List<List<Integer>> edge = new ArrayList<List<Integer>>();
int nodeNum = 0;
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
for (String word : wordList) {
addEdge(word);
}
addEdge(beginWord);
if (!wordId.containsKey(endWord)) {
return 0;
}
int[] disBegin = new int[nodeNum];
Arrays.fill(disBegin, Integer.MAX_VALUE);
int beginId = wordId.get(beginWord);
disBegin[beginId] = 0;
Queue<Integer> queBegin = new LinkedList<Integer>();
queBegin.offer(beginId);
int[] disEnd = new int[nodeNum];
Arrays.fill(disEnd, Integer.MAX_VALUE);
int endId = wordId.get(endWord);
disEnd[endId] = 0;
Queue<Integer> queEnd = new LinkedList<Integer>();
queEnd.offer(endId);
while (!queBegin.isEmpty() && !queEnd.isEmpty()) {
int queBeginSize = queBegin.size();
for (int i = 0; i < queBeginSize; ++i) {
int nodeBegin = queBegin.poll();
if (disEnd[nodeBegin] != Integer.MAX_VALUE) {
return (disBegin[nodeBegin] + disEnd[nodeBegin]) / 2 + 1;
}
for (int it : edge.get(nodeBegin)) {
if (disBegin[it] == Integer.MAX_VALUE) {
disBegin[it] = disBegin[nodeBegin] + 1;
queBegin.offer(it);
}
}
}
int queEndSize = queEnd.size();
for (int i = 0; i < queEndSize; ++i) {
int nodeEnd = queEnd.poll();
if (disBegin[nodeEnd] != Integer.MAX_VALUE) {
return (disBegin[nodeEnd] + disEnd[nodeEnd]) / 2 + 1;
}
for (int it : edge.get(nodeEnd)) {
if (disEnd[it] == Integer.MAX_VALUE) {
disEnd[it] = disEnd[nodeEnd] + 1;
queEnd.offer(it);
}
}
}
}
return 0;
}
public void addEdge(String word) {
addWord(word);
int id1 = wordId.get(word);
char[] array = word.toCharArray();
int length = array.length;
for (int i = 0; i < length; ++i) {
char tmp = array[i];
array[i] = '*';
String newWord = new String(array);
addWord(newWord);
int id2 = wordId.get(newWord);
edge.get(id1).add(id2);
edge.get(id2).add(id1);
array[i] = tmp;
}
}
public void addWord(String word) {
if (!wordId.containsKey(word)) {
wordId.put(word, nodeNum++);
edge.add(new ArrayList<Integer>());
}
}
}
时间复杂度: O(N×C^2)。其中N为wordList的长度,C为列表中单词的长度。
1、建图过程中,对于每一个单词,我们需要枚举它连接到的所有虚拟节点,时间复杂度为O(C),将这些单词加入到哈希表中,时间复杂度为O(N×C),因此总时间复杂度为O(N×C)。
2、双向广度优先搜索的时间复杂度最坏情况下是O(N×C)。每一个单词需要拓展出O(C)个虚拟节点,因此节点数O(N×C)。
空间复杂度: O(N×C^2)。其中N为wordList的长度,C为列表中单词的长度。哈希表中包含O(N×C)个节点,每个节点占用空间O(C),因此总的空间复杂度为O(N×C^2)。