接上文,本章将两个比较重要的非理想因素,因此各项指标制定。后续会对常见的非理想因素给出常见的解决方法,以及设计所采用的方法。
2.2.3. 比较器失调
在流水线 ADC 中,比较器的主要误差来源就是比较器失调,称为失调误差(Offset Error)。比较器失调通常由工艺偏差和交叉耦合导致的不对称所导致,所以几乎无法避免。失调误差会使得比较器比较电平发生偏移,有可能会导致误码,甚至丢码。泛采用冗余校准技术,这大大降低了对比较器失调误差的要求,但仍需使失调误差在校准允许的范围内,同时也要保证比较器的工作速度。
比较器的输入失调电压通常在几十至几百毫伏之间,因此其对子 ADC 整体输出结果产生的影响是不容小觑的。当前解决比较器输入失调电压过大的方法普遍是在前级加入放大器,虽然加入前置比较器会引入更大的功耗,但是对于流水线 ADC 来说,对于 ADC 的位数要求并不高,通常不会超过 4 位,因此加入前置放大器是一个比较合适的方案,既可以降低比较器的输入失调电压,并且也可以作为隔离消除噪声。
发生比较器阈值电压误差的 1.5bit MDAC 传输曲线如图所示,实线表示理想情况,虚线表示误差下的情况。

图 18 存在比较器阈值电压误差的MDAC传输曲线
数字校正算法的分析,这种算法对于比较器的失调电压提供了更加宽松的设计要求。假设一个比较器失调电压为 Vos,如图所示:

图 19 比较器示意图
以 1.5 位子级为例,第 i 级的参考电平设为-1/4Vref 与+1/4Vref,即 Vr1=-1/4Vref,Vr2=+1/4Vref。实际的比较器在应用中,必然存在失调电压 Vos,这里将比较器的误差用参考电平误差来表示,即 Vr1=-1/4Vref+Vos1,Vr2=+1/4Vref+Vos1,当 Vr,i满足式:

此时该级出现的量化误差即为+1 或-1,输出的余量误差可以表示为-Vref或+Vref。如果 Vr,i不在上述范围,该级将不会产生上述误差。
下面详细推导数字校正算法中如何消除比较器的失调,对于第 i 级,假设输入:
![]()
当第 i+1 级为理想比较器时,该级所的到得量化值 Di+1*=2 余量为:
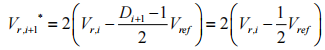

可得出:
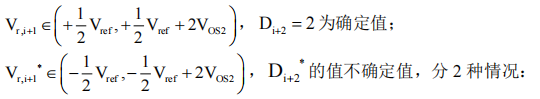
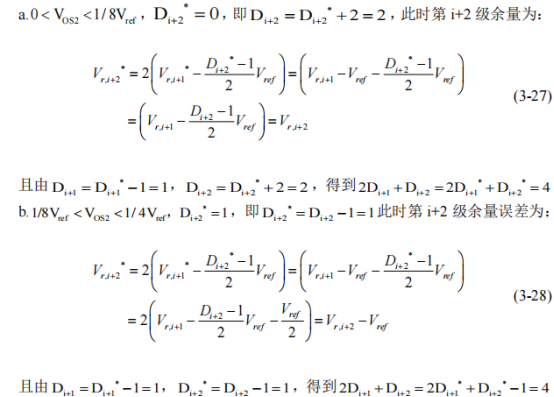
综上所述可以得出当流水线采用 1.5 位的子级模块,将比较器的失调电压等效到参考电平的误差,只要该误差值满足一定条件,通过数字校正算法可以进行消除。在电路设计过程中,只要保证比较器失调电压在一定范围内,就不会导致 ADC 量化结果产生误差。
如图所示,如果 |Vos|>1/4*Vref ,该级的余量会超出下一级比较器的量化范围,所以为了不产生量化结果的误差,比较器失调电压必须满足 |Vos|<1/4*Vref 。

图 20 1.5 位子级失调电压示意图
上述推导过程为 1.5 位子级的比较器需要满足的失调电压要求,同理可以推导出本设计采用的 2.5 位子级中对于比较器失调电压的指标要求为:
![]()
2.2.3. 放大器误差
由于实际运放的直流增益以及带宽均为有限值。对于一个运放的闭环系统,运放的直流增益决定了该反馈系统的输出精度,带宽则决定了运放的建立时间,输出要在规定时间内完整建立信号。实际的运放不可能做到理想情况,增益和带宽是有限的,则会造成电路中存在误差。运放的性能决定了 MDAC 电路的性能。
在非理想情况下,运算放大器的增益、带宽以及摆幅都是有限的,还会有失调和噪声,在考虑这些非理想因素的情况下,设 A 为运算放大器开环增益,Vos 为运放输出失调电压,Vn为运放输出总噪声,β 为反馈系数,由运算放大器工作原理可得:

上式中划线部分是理想的输出。其中静态误差和动态误差分别为:

静态误差主要由于运放的开环增益 A 有限而引起的,动态误差则是源于有限的运放带宽。对于 MDAC 电路而言,要想输出精度满足设计指标,要求两种误差之和小于系统总误差。
(1)静态建立误差
对于一个闭环系统,假设运放的直流增益为 A,闭环系统的反馈系数为 β。其传输函数可以表示为:

该闭环系统的误差为:
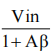
对于本课题中采样保持电路和 MDAC 中的运放,Aβ 远大于 1。同时,由于电路在满摆幅 VFS 时有最大的误差,且 VFS=1V。所以,由运放有限增益带来的误差近似为:
![]()
对于流水线 ADC,为了设计时留有裕量,一般要求误差绝对值小于剩余精度的 1/4LSB,即:

对于流水线不同子级,根据电路结构以及流水线架构,存在不同的 β 值和 N。其中采样保持电路反馈系数 β 为 1/2,在流水线子级的 MDAC 中,反馈系数则为 1/4。由于每一级都会有部分数字码完成转换,所以越靠后的子级,需要达到的精度越低。对于本设计的流水线结构,每级有两位二进制码完成转换,每一级 N 的值减小 2。由此可以计算出每一级所使用的运放所需要的直流增益。
下图为有限增益下 1.5bit MDAC 传输函数曲线,可见实际曲线斜率略小于理想情况。

图 21 运放有限增益误差下的MDAC输出
下图是考虑到运放增益非线性影响下的 1.5bit MDAC 的输出曲线。当运放第 二级的差分输出为 0,即 2 个输出端电平为VCM时,运放开环增益最大;输出越偏离 VCM,开环增益越低。表现为 MDAC 输出曲线越偏离 0,其斜率越低。考虑到为了降 低增益非线性的影响,应该减小第二级输出管的过驱动电压,避免满摆幅输出时第二 级输出管接近线性区引起增益大幅下降。

图 22 运放增益非线性下的MDAC输出
(2)动态建立误差
通常来说 MDAC 的工作过程中离不开对电容的充放电过程,然而电荷的存储和 泄放均需要时间,这也使得电容极板电位不可能产生突变,必然是一个缓慢变化的过程,从变化开始到电平稳定需要一定的建立时间。但流水线 ADC 受到时钟的控制,这就要求其需要在有限的时间周期内完成信号建立,因此该建立时间同时钟周期的相互制约便引入了有限建立误差。

图 23 输出建立不完全下MDAC传输曲线
在流水线 ADC 中,运放的输出信号要在给定的时钟下完成信号建立。运放的有限带宽也会影响到输出信号的建立,这种误差叫做不完全建立误差。当输入为一个大的阶跃信号,输出信号的建立可以分为两个过程,即大信号建立和小信号建立。其中小信号建立与运放的增益带宽有关,大信号建立则与运放的摆率有关。信号的建立过程如图所示:
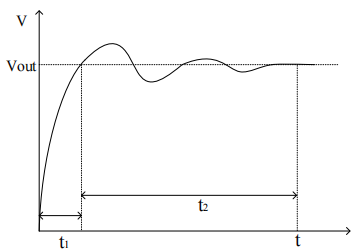
图 24 运放建立过程示意图
其中 t1、t2 分别为大信号建立时间(和压摆率SR有关)和小信号建立时间(和带宽有关),通常情况下,小信号建立时间更长,这里假设 t1 与 t2 的比为 1:3,运放的总建立时间为 t。为了满足建立精度,输出要在时钟信号的半周期内(t =Ts / 2)完成建立。
a. 大信号建立
在 MDAC 工作过程中,运放首先进入大信号工作状态,建立起静态工作点,然后开始小信号放大。大信号建立的速度主要取决于压摆率(Slew Rate)的大小,一般来说大信号建立时间应小于 T/3,但实际上为了小信号的稳定,大信号建立时间应该越小越好,带宽的大小决定了小信号建立的速度。将 MDAC 中的运放视为一个单极点系统,其压摆率为:
![]()
其中 CL是运放总负载电容,Is 是输出电流,由此可见,电流越大、负载电容越小,运放的压摆率越大,其大信号建立时间也更短。
(对于大信号压摆率,根据网上搜罗的,如果采用二级运放的话,压摆率如下,总之就是电流要大,电容要小)
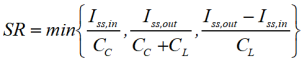
b. 小信号建立
由有限带宽导致的小信号建立误差同样可以由此单极点系统来近似,在只考虑运放带宽非理想因素的情况下,其传输函数为:

其中 Vout,id 是理想输出,ts 为小信号建立时间,一般要求 ts 小于时钟周期的一半,但实际上,为了后级流水级能够较好的采样到准确的输出信号,ts 越小越好,通常取 ts<1/3T,τ 是建立时间常数,它是运放闭环单位增益带宽 βωu 的倒数,ωu 是运放开环带宽。
则系统的建立误差可以表示为:
![]()
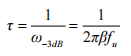
ω-3dB为系统的-3dB 带宽,fu 为运放单位增益带宽。为了满足 ADC 精度要求以及留出设计裕量,小信号建立误差要求小于 1/4LSB,假设小信号建立完成需要的时间为 tset,则有:

VFS为 1V,N 为该子级需要达到的精度。由此可以得出,时常数 τ 应该满足式:
![]()
进而推导出运放的单位增益带宽应该满足:
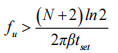
(注意这里的VFS为1V,若范围有变的话,带宽要求是不一样的)
从上述分析中可以看出,运放小信号建立的过程中,输出信号之中多了一个指数项,运放闭环单位增益带宽越大,达到相应精度所需的时间越少,建立误差越小,但带宽越大也会带来更多的功耗和噪声,需要依据实际需求进行折中。
还需要注意的是,这个单位增益带宽是以假设运放是单级点系统计算得出的,实际运放由于次级点,第三极点等影响,单位增益带宽会变低,而运放工作时始终是闭环状态,因此只用保证运放的闭环带宽达到要求,对单位增益带宽的设计可放松要求,以减小设计难度以及运放的功耗。
====未完待续====