文章目录
- 前言
- 查找
- 搜索二叉树的结构
- insert
- find
- erase
- 递归版本
- Find
- insert
- erase
- 二叉树的拷贝问题
- 搜索二叉树的应用
- Key模型
- Key/Value的模型
前言
普通二叉树其实意义不大,
如果用二叉树存储数据的话,还不如顺序表,链表这些。
搜索二叉树它的意义就很大了。
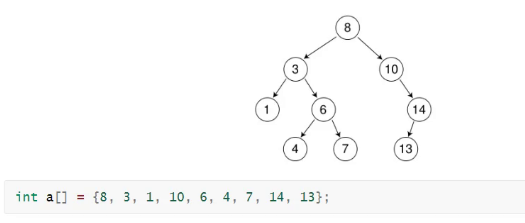
左边比根小,右边比根大,子树也满足这个特征。
查找
搜索二叉树查找一个值怎么找?
根比它大就往左边走,比它小就往右边走。
搜索二叉树还有一个特征:
走中序是怎么样子的。升序的一个状态。
所以搜索二叉树也叫做排序二叉树,或者二叉排序树。
搜索二叉树的结构

我们一般在类里面typedef,因为在外面容易冲突,在里面受类域的限制。
insert
搜索二叉树第一步插入,这里又回到我们以前学的知识了,还是比较简单了。
**insert有成功也有失败,
搜索二叉树插入具有非常大的意义,因为搜索二叉树是一个功能性非常强的数据结构,
它可以很便捷的进行一个查找。
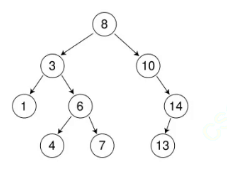
假设我要插入12,插入12很好找,因为它是确定的,一个指针往下走就可以了。

搜索二叉树插入位置是非常确定的,普通二叉树插在哪都不知道,
所以搜索二叉树的增删查改比较有意义
假设我要插入13呢?
13插入失败,因为默认的搜索二叉树也是不允许冗余的,这值已经有了,再存就没有意义了。
再回答一个问题,根的值是怎么来的?
它是一个数一个数插入的,插入的第一个值就是根。
所以同样是1,2,3,插入顺序不同形状就不同。
如果一上来就是最小的值,那不是歪脖子了吗?
后面讲到的平衡二叉树专治这种病。
确定插入的是第一个结点
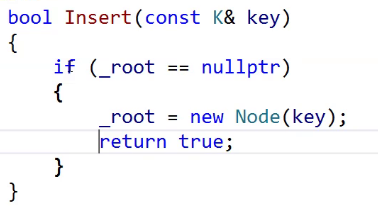
找空位置:

找到空以后:
给大家看一种错误的写法
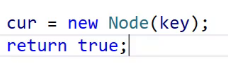
cur是一个局部变量,出了作用域找不到12的结点,还没有链接起来
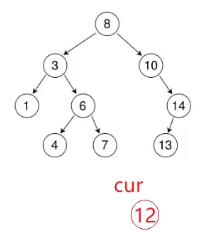
怎么记录它的父亲呢?
前后指针往下走,然后处理一下。
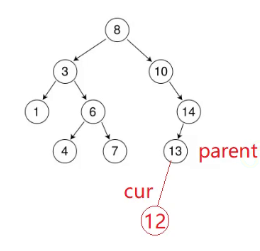
跟它的父亲左边链接还是右边链接?
还得比较一下。
最后测试一下:
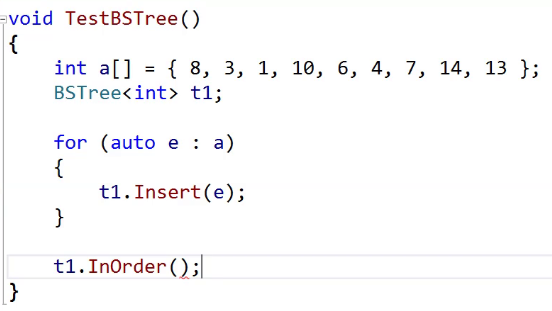
但是当前这个函数不好调,因为要调用InOrder得传根指针,但是访问不到根。

InOrder可以访问到_root,但是不加参数它没办法访问到子树,所以必须要有参数。
怎么解决呢?
C++的成员函数只要是要写递归都建议再套上一层。
因为你要写递归,你就必须要传参数,但是用惯例传参数又会很恶习。

给缺省的性不行?

报错。

缺省值必须是全局变量或者是常量。(全局变量不一定是常量,搞成静态的就可以)
你要访问成员变量得用this,这个位置没有this指针。
this指针是形参,形参不一定传过来了。只能在函数内部才能用this指针
紧接着的报错信息


这里要写构造函数。
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
// 链接
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
}

find
find就相当简单了。
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
erase
删除才是重点。
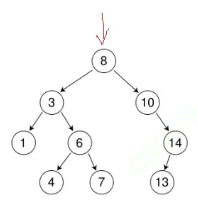
假设我要删除4:
删除4很好删,可以找到4,或者找到4的父亲,然后置空

6和14要怎么删:
删除6的话,找到6好删,6只有一个孩子。
一个父亲最多有两个孩子,可以领养。删除14也是一样。
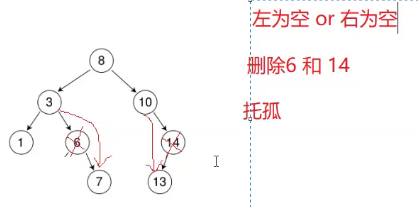
删除3和8:
3不好删,3有2个孩子,8管不住3个孩子.
那怎么办?
这就相当于自己要去上班,有两个孩子也不能给父亲托管。
那可以请保姆去管这两个娃,请的这个保姆得能管这两个娃。
有人想把数据删除然后把后面的数据重新插入,那这样太麻烦了。
假设要删除的是8,请谁能管这颗树呢?
很简单,比左边大比右边小就可以。有两个地方的值适合。
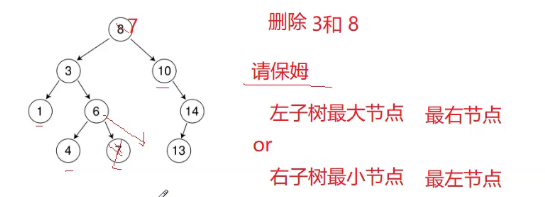
把父亲记录下来,托孤的话,要给父亲,有父亲更好处理

上面可以把第一种情况和第二种情况合并到一起来处理,归类的更少代码更简洁一点。
都可以当作
左为空,父亲指向我的右。
右为空,父亲指向我的左。
写代码
找要删除的值:
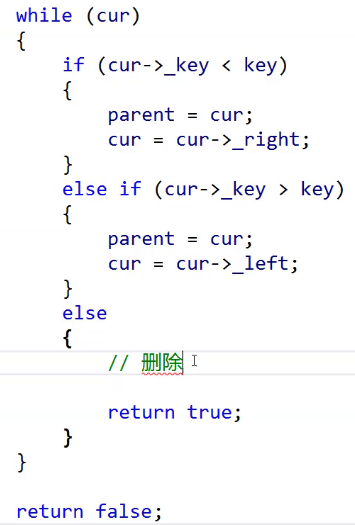
第一种情况,左为空
左位空,不能确定父亲的什么指向我的右,判断一下。

分析问题的时候,不能以特例来分析问题,不然出bug,然后调试又要花帮半天
你要去反驳,一定是这个吗,刻意去找到反驳的理由
第二种情况,右为空
跟上面一样的道理
第二种情况,左右都不为空
左右都不为空,不敢托孤,去找替代结点。
这里用右树最小结点。

这个时候就转换成删
给大家看两种情况,稍不注意容易被坑。
1.它是左为空,它可能右边不为空。它不一定是叶子。
那删除这个叶子怎么删?(你要找保姆,保姆也有可能有孩子,你要找的这个保姆的特征
是能帮你带两个孩子)
保姆不能有两个孩子,保姆如果有一个孩子可以托孤给父亲带,同时它替代给你帮你带。
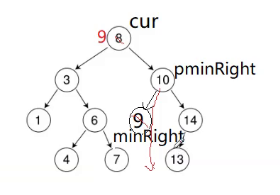
保姆的孩子一定是托给父亲的左吗?
这个地方有一个大坑。面对上面这个场景可以解决,但是面对下面这个场景解决不了。
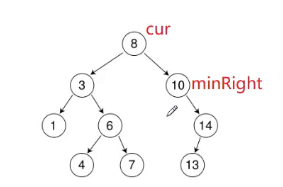
minRight的左是空,导致找右树最小结点这个循环不会进去,
它还到最一个后果:
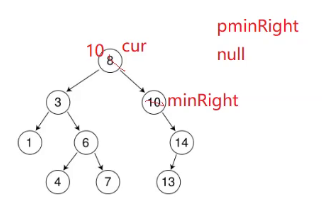
怎么办?
//Node* pminRight =nullptr;error
Node* pminRight = cur;
这个时候循环的可能不会进去,右树的最小结点就是右树的根。
这里也不可以这样写。
最左结点不一定是父亲的左。

这就是极端场景。怎么办呢?判断一下。

教大家怎么测试自己程序写的对不对?
就找特殊值删

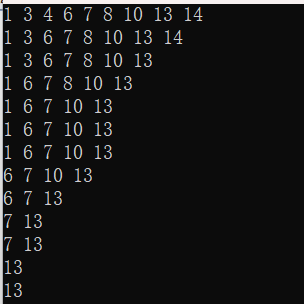
这个代码还是有些问题的。
如果你的代码能删除8,就能证明是逻辑上没问题的
我们的代码还有一个小问题,
这种情况会崩
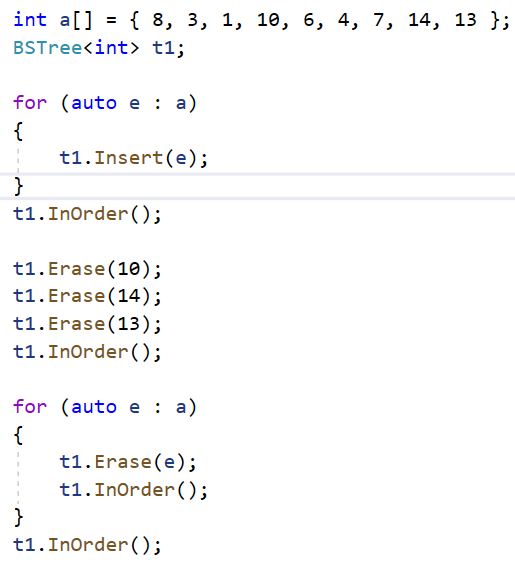
注意看,parent为NULL

删除8的时候出问题了。可以调试看一下
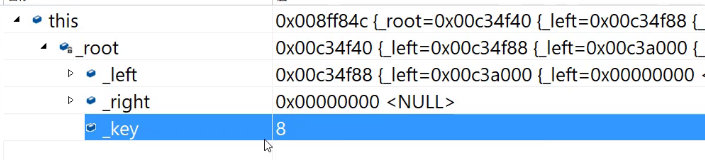
它的右边是空,左边有结点。大概是这样。

这个时候怎么处理一下?
这里是没有父亲。
这里把8删除了,应该更新一下root.
去左子树找一个最大的结点去替代也是可以的。
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 删除
// 1、左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
} // 2、右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// 找右树最小节点替代,也可以是左树最大节点替代
Node* pminRight = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
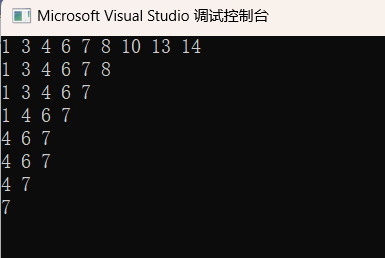
现在好了。
递归版本
搜索二叉树能用循环就用循环,递归深度太深有一些栈溢出等等的问题。
Find

子问题:如果比8大我就转换成去比右子树查找。
如果比小大我就转换成去比左子树查找。
这跟以前二叉树的先序不同的是,不是整颗树都要遍历。
public:
bool FindR(const K& key)
{
return _FindR(_root, key);
}
protected:
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key == key)
return true;
if (root->_key < key)
return _FindR(root->_right, key);
else
return _FindR(root->_left, key);
}
insert
刚才的不值得我们细细的看,但是现在这个还是要求我们仔细看的。
我们要在搜索树里进行插入。
比它大我就往左边走,比它小我就往右边走。
如果要插入16,怎么插入?
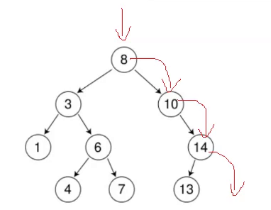
前面都比较好处理,但是我插入要跟父亲链接起来,如何跟父亲链接起来。

root是一个局部变量。
第一种方案,把父亲传过来。
第二种方案,不要走到空,而是比它大右边为空就插入。
这两个方案都不是最好的方案。
最好的方案是用一个引用解决这个问题。
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
这个写法非常非常牛,还能这样玩?
new的这个结点直接给root就链接上了。
画一个递归展开图就非常清楚。
假设root是一颗空树

这很好理解。
现在要插入16,我这里就先不画了,有兴趣的可以自己画一下这个递归展开图。
这个引用恰到好处,不用判断我是父亲的左还是父亲的右,我就是父亲那个左指针/右指针的别名。
不用判断父亲,不用处理各种问题。
前面的循环引用不可以,因为这里存在一个问题。C++的引用不能改变指向。
这里可以用是因为每个栈帧里面都是一个新的引用。
erase
删除也很好搞。
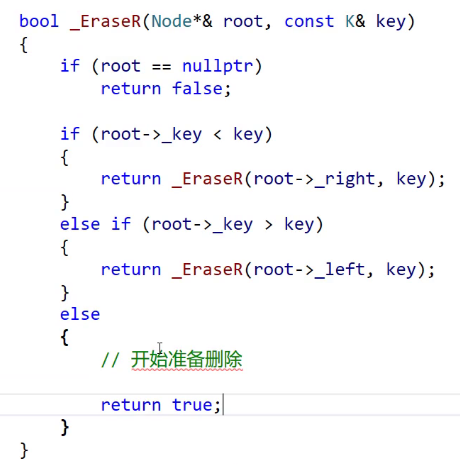
怎么删呢?
还是要分为三种情况。
这里左右不为空的情况很容易被卡住。
首先,这里如果左为空,让父亲指向你的右,
如果右为空,让父亲指向你的左,这个跟之前值一样的。
假设我要删14:

我现在要让父亲指向我的左。怎样找父亲?
不需要传,root是14的指针,也是10的右的指针的别名。让root指向13就可以了。
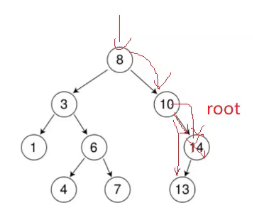

这里就很容易卡住了
一直想着试图用引用但是引用又用不上。
假设我要上的是8.
我这里要用左树的最大结点来替代。

第一种方式
记录父亲,然后判断去删
还有一种方式
再去做一次子递归,这种方式是最简洁的。
替代之后,怎么删呢?
递归转换成在左子树去删除key就可以了。
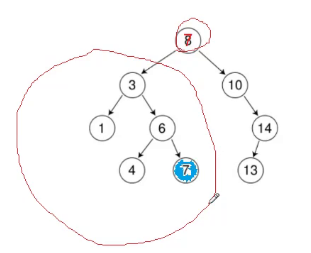
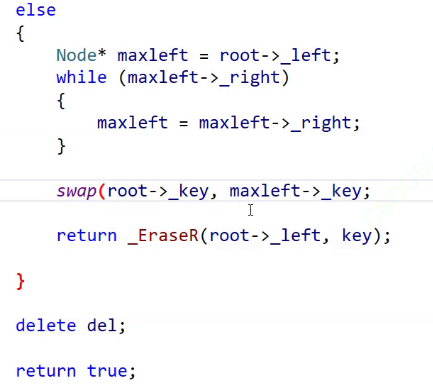
这里一定会转换成前面两种的一种。
因为你这里要删除的结点一定是左为空或者右为空。
记住这里一定要传root->_left,但是不能传maxleft,不然会出问题。
因为要用引用,如果直接传maxleft,引用不起作用。
这个delete是一定可以执行到的。-
之前写的循环版本能不能转化成子问题删除?
不能,因为他没有条件,递归调自己没办法传这个根。
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
// 开始准备删除
if (root->_right == nullptr)
{
root = root->_left;
}
else if (root->_left == nullptr)
{
root = root->_right;
}
else
{
Node* maxleft = root->_left;
while (maxleft->_right)
{
maxleft = maxleft->_right;
}
swap(root->_key, maxleft->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
二叉树的拷贝问题
二叉树的拷贝暂时是没问题的,因为我们还没有写析构。
它是个浅拷贝。


我们要写深拷贝。
先把析构给写了。
析构可以用循环来写,但是比较麻烦,用递归来写。
跟以前一样,写一个递归的后序删除就可以了。
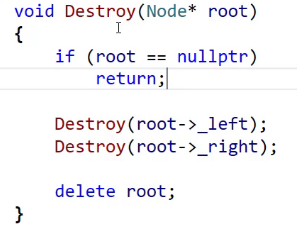
有人是这样写的,能看懂这是啥意思吗?
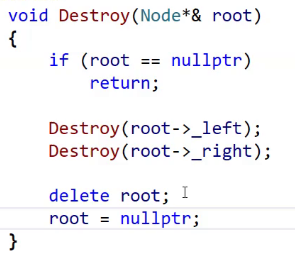
对最外层来说,root就是_root的别名。里面置空外面就跟着置空了。

但是出现了一个野指针问题,为什么?
因为前面写了一个浅拷贝。我们要写一个深拷贝。
深拷贝的拷贝构造还是一样,一个结点一个结点的拷贝。这里推荐用递归去写。
用一个前序的思想

前序在创建,后序在链接。
拷贝构造就直接调用了

写了拷贝构造我们就的把构造写一下,构造的特性就是我们不写编译器就会默认生成构造,
拷贝构造也是构造,编译器就不会生成了。
还得自己再写一个构造

赋值
赋值我们就用现代写法了。
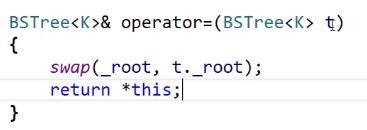
/*BSTree()
:_root(nullptr)
{}*/
BSTree() = default; // 制定强制生成默认构造
BSTree(const BSTree<K>& t)
{
_root = Copy(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
~BSTree()
{
Destroy(_root);
//_root = nullptr;
}
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* newRoot = new Node(root->_key);
newRoot->_left = Copy(root->_left);
newRoot->_right = Copy(root->_right);
return newRoot;
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
时间复杂度
搜索二叉树增删查改的时间复杂度是多少?
lgN是相对比较理想的情况,我们不能根据这个。
它可能很不均衡,像下面中间,比如我以有序或者接近有序去插入。
最右边,N/2还是N
所以二叉树功能不错,但是底线没有保障。
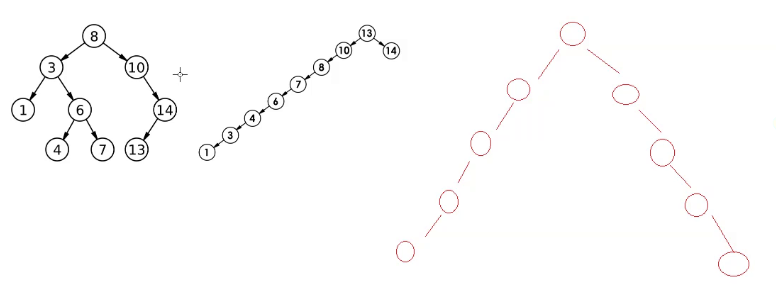
所以把搜索二叉树的时间复杂度定位O(N).
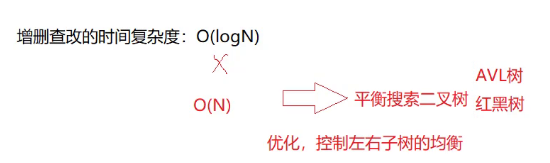
搜索二叉树的应用
Key模型
它这里的模型指的是应用搜索场景。

Key/Value的模型

接下来给大家演示一下key/value的场景
怎么办呢?
就是这棵树里面既要有key,又要有value。
首先看我们之前写的代码,其他地方都不变,模板参数多了一个value
这个的本质在于查找还是按以前的,这棵树还是以前的搜索二叉树,
还是按以前的key走,但是找到key就找到这个value,
因为key和value是存在同一个结点的。
namespace key_value
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
// 链接
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 删除
// 1、左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
} // 2、右为空
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
// 找右树最小节点替代,也可以是左树最大节点替代
Node* pminRight = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
pminRight = minRight;
minRight = minRight->_left;
}
cur->_key = minRight->_key;
if (pminRight->_left == minRight)
{
pminRight->_left = minRight->_right;
}
else
{
pminRight->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
protected:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
}

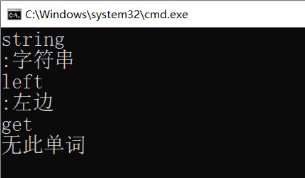
怎么结束呢?
1.CTRL C
2.推荐CTRL Z+换行
还有一个问题
这里有一堆水果,统计水果出现的次数,怎么完?
这是一个比较晦涩一点的场景。


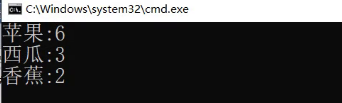
这里为什么没有排序?
这里是中文,它是按照Ascii排的。