第四章 机器学习
十二、逻辑回归
1. 概述
1.1 什么是逻辑回归
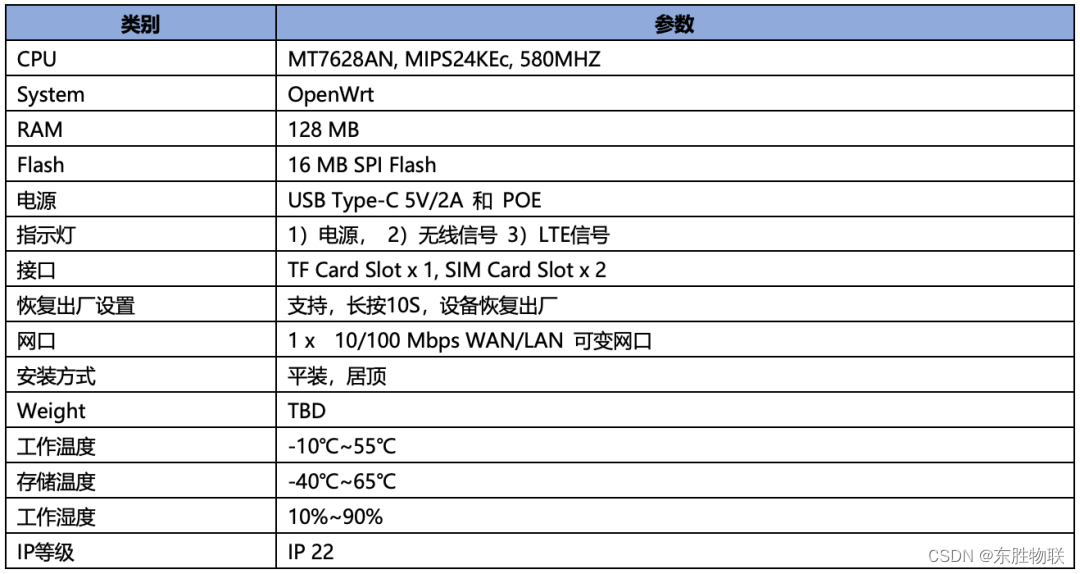
逻辑回归(Logistic Regression) 虽然被称为回归,但其实际上是分类模型,常用于二分类。逻辑回归因其简单、可并行化、可解释强而受到广泛应用。二分类(也称为逻辑分类)是常见的分类方法,是将一批样本或数据划分到两个类别,例如一次考试,根据成绩可以分为及格、不及格两个类别,如下表所示:
| 姓名 | 成绩 | 分类 |
|---|---|---|
| Jerry | 86 | 1 |
| Tom | 98 | 1 |
| Lily | 58 | 0 |
| …… | …… | …… |
这就是逻辑分类,将连续值映射到两个类别中。
- 根据样本数据,构建一个线性回归模型,预测输出(连续)
- 将连续的预测数据,代入到逻辑函数中
- 逻辑函数,将预测值映射到 0-1 区间范围内(将线性转为非线性)
- 找到一个阈值 0.5
- 大于 0.5 --> 1,小于 0.5 --> 0
1.2 逻辑函数
逻辑回归是一种广义的线性回归,其原理是利用线性模型根据输入计算输出(线性模型输出值为连续),并在逻辑函数作用下,将连续值转换为两个离散值(0 或 1),其表达式如下:
y = h ( w 1 x 1 + w 2 x 2 + w 3 x 3 + . . . + w n x n + b ) y = h(w_1x_1 + w_2x_2 + w_3x_3 + ... + w_nx_n + b) y=h(w1x1+w2x2+w3x3+...+wnxn+b)
其中,括号中的部分为线性模型,计算结果在函数 h ( ) h() h()的作用下,做二值化转换,函数 h ( ) h() h()的定义为:
h = 1 1 + e − t h= \frac{1}{1+e^{-t}} h=1+e−t1
t = w T x + b \quad t=w^Tx+b t=wTx+b
该函数称为 Sigmoid 函数(又称逻辑函数),能将 ( − ∞ , + ∞ ) (-\infty, +\infty) (−∞,+∞)的值映射到 ( 0 , 1 ) (0, 1) (0,1)之间,其图像为:
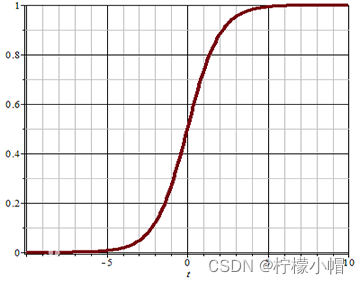
可以设定一个阈值(例如 0.5),当函数的值大于阈值时,分类结果为 1;当函数值小于阈值时,分类结果为 0。也可以根据实际情况调整这个阈值。
1.3 分类问题的损失函数
对于回归问题,可以使用均方差作为损失函数,对于分类问题,如何度量预测值与真实值之间的差异?分类问题采用交叉熵作为损失函数,当只有两个类别时,交叉熵表达式为:
E ( y , y ^ ) = − [ y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ] E(y, \hat{y}) = -[y \ log(\hat{y}) + (1-y)log(1-\hat{y})] E(y,y^)=−[y log(y^)+(1−y)log(1−y^)]
其中,y 为真实值, y ^ \hat{y} y^为预测值。
- 当 y = 1 y=1 y=1时,预测值 y ^ \hat{y} y^越接近于 1, l o g ( y ^ ) log(\hat{y}) log(y^)越接近于 0,损失函数值越小,表示误差越小,预测的越准确;当预测时 y ^ \hat{y} y^接近于 0 时, l o g ( y ^ ) log(\hat{y}) log(y^)接近于负无穷大,加上符号后误差越大,表示越不准确;
- 当 y = 0 y=0 y=0时,预测值 y ^ \hat{y} y^越接近于 0, l o g ( 1 − y ^ ) log(1-\hat{y}) log(1−y^)越接近于 0,损失函数值越小,表示误差越小,预测越准确;当预测值 y ^ \hat{y} y^接近于 1 时, l o g ( 1 − y ^ ) log(1-\hat{y}) log(1−y^)接近于负无穷大,加上符号后误差越大,表示越不准确.
2. 逻辑回归实现
sklearn 中,逻辑回归相关 API 如下:
# 创建模型
# solver参数:逻辑函数中指数的函数关系(liblinear表示线性关系)
# C参数:正则强度,越大拟合效果越小,通过调整该参数防止过拟合
model = lm.LogisticRegression(solver='liblinear', C=1)
# 训练
model.fit(x, y)
# 预测
pred_y = model.predict(x)
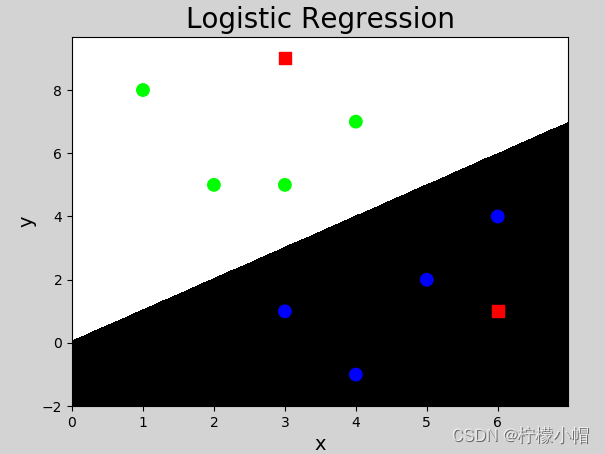
以下是使用 sklearn 库提供的逻辑分类器(LogisticRegression)实现的代码:
# 逻辑分类器示例
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
x = np.array([[3, 1], [2, 5], [1, 8], [6, 4],
[5, 2], [3, 5], [4, 7], [4, -1]])
y = np.array([0, 1, 1, 0, 0, 1, 1, 0])
# 创建逻辑分类器对象
model = lm.LogisticRegression()
model.fit(x, y) # 训练
# 预测
test_x = np.array([[3, 9], [6, 1]])
test_y = model.predict(test_x) # 预测
print(test_y)
# 计算显示坐标的边界
left = x[:, 0].min() - 1
right = x[:, 0].max() + 1
buttom = x[:, 1].min() - 1
top = x[:, 1].max() + 1
# 产生网格化矩阵
grid_x, grid_y = np.meshgrid(np.arange(left, right, 0.01),
np.arange(buttom, top, 0.01))
print("grid_x.shape:", grid_x.shape)
print("grid_y.shape:", grid_y.shape)
# 将x,y坐标合并成两列
mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
print("mesh_x.shape:", mesh_x.shape)
# 根据每个点的xy坐标进行预测,并还原成二维形状
mesh_z = model.predict(mesh_x)
mesh_z = mesh_z.reshape(grid_x.shape)
mp.figure('Logistic Regression', facecolor='lightgray')
mp.title('Logistic Regression', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, mesh_z, cmap='gray')
mp.scatter(x[:, 0], # 样本x坐标
x[:, 1], # 样本y坐标
c=y, cmap='brg', s=80)
mp.scatter(test_x[:, 0], test_x[:, 1], c="red", marker='s', s=80)
mp.show()
"""
[1 0]
grid_x.shape: (1100, 700)
grid_y.shape: (1100, 700)
mesh_x.shape: (770000, 2)
"""
执行结果:
3. 多分类实现
逻辑回归产生两个分类结果,可以通过多个二元分类器实现多元分类(一个多元分类问题转换为多个二元分类问题)。如有以下样本数据:
| 特征 1 | 特征 2 | 特征 3 | 实际类别 |
|---|---|---|---|
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | A |
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | B |
| x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | C |
进行以下多次分类,得到结果:
第一次:分为 A 类(值为 1)和非 A 类(值为 0)
第二次:分为 B 类(值为 1)和非 B 类(值为 0)
第三次:分为 C 类(值为 1)和非 C 类(值为 0)
……
以此类推。
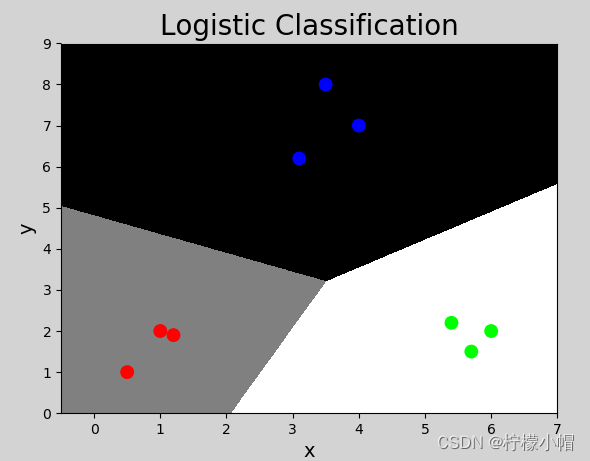
利用逻辑分类器实现多元分类示例代码如下:
# 多元分类器示例
import numpy as np
import sklearn.linear_model as lm
import matplotlib.pyplot as mp
# 输入
x = np.array([[4, 7],
[3.5, 8],
[3.1, 6.2],
[0.5, 1],
[1, 2],
[1.2, 1.9],
[6, 2],
[5.7, 1.5],
[5.4, 2.2]])
# 输出(多个类别)
y = np.array([0, 0, 0, 1, 1, 1, 2, 2, 2])
# 创建逻辑分类器对象
model = lm.LogisticRegression(C=200) # 调整该值为1看效果
model.fit(x, y) # 训练
# 坐标轴范围
left = x[:, 0].min() - 1
right = x[:, 0].max() + 1
h = 0.005
buttom = x[:, 1].min() - 1
top = x[:, 1].max() + 1
v = 0.005
grid_x, grid_y = np.meshgrid(np.arange(left, right, h),
np.arange(buttom, top, v))
mesh_x = np.column_stack((grid_x.ravel(), grid_y.ravel()))
mesh_z = model.predict(mesh_x)
mesh_z = mesh_z.reshape(grid_x.shape)
# 可视化
mp.figure('Logistic Classification', facecolor='lightgray')
mp.title('Logistic Classification', fontsize=20)
mp.xlabel('x', fontsize=14)
mp.ylabel('y', fontsize=14)
mp.tick_params(labelsize=10)
mp.pcolormesh(grid_x, grid_y, mesh_z, cmap='gray')
mp.scatter(x[:, 0], x[:, 1], c=y, cmap='brg', s=80)
mp.show()
执行结果:
4. 总结
-
逻辑回归是分类问题,用于实现二分类问题
-
实现方式:利用线性模型计算,在逻辑函数作用下产生分类
-
多分类实现:可以将多分类问题转化为二分类问题实现
-
用途:广泛用于各种分类问题