力扣日记:【二叉树篇】501. 二叉搜索树中的众数
日期:2023.12.23
参考:代码随想录、力扣
501. 二叉搜索树中的众数
题目描述
难度:简单
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
示例 1:
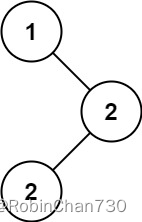
输入:root = [1,null,2,2]
输出:[2]
示例 2:
输入:root = [0]
输出:[0]
提示:
- 树中节点的数目在范围 [1, 10^4] 内
- -10^5 <= Node.val <= 10^5
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
TreeNode* pre = nullptr;
vector<int> result;
int maxCount = 1;
int count = 1;
public:
vector<int> findMode(TreeNode* root) {
traversal(root);
return result;
}
void traversal(TreeNode* root) {
// 左中右
if (root == nullptr) return;
// 左
traversal(root->left);
// 中
if (pre != nullptr) {
if (root->val == pre->val) {
// 相等, count++
count++;
} else {
count = 1; // 重新置为1
}
}
pre = root;
if (count == maxCount) { // 如果当前计数与maxCount一致,说明可能是众数,放入数组中
result.push_back(root->val);
} else if (count > maxCount) { // 如果比maxCount大了,说明当前数才是新的众数,清空原来数组,加入当前数
maxCount = count;
result.clear();
result.push_back(root->val);
}
// 右
traversal(root->right);
}
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 这次没看代码随想录就能跟其思路基本一致,有点小开心2333(ww对我来说太难得了)
- 对于二叉搜索数,中序遍历的时候是有序的,相当于处理有序数组一样,如何在一次遍历的时候就能找到所有众数呢?关键的有两点:
- 1.如果遍历到当前值,count==maxCount了,就将其当作可能的众数,加入结果集中
- 2.但是一旦发现当前值的count>maxCount,说明当前值才是新的唯一的众数,要清空原先的结果集,再把当前值加入
- 本题同样注意要用 pre 来记录上一个节点,且这里为了方便,将count、maxCount、pre和result都作为全局变量了
- 另外的解法:
- 也可以遍历两遍:第一遍找到maxCount;第二遍记录count为maxCount的所有值
- 对于不是二叉搜索树的,要先遍历一遍树,用map统计频率,把频率排个序,最后取前面高频的元素的集合。
- 1.遍历树,用map统计频率
- 2.把统计的出来的出现频率(即map中的value)排个序(要把map转化数组即vector,再进行排序)
- 3.取前面高频的元素
- 具体见代码随想录