A Cluster Separation Measure(一种聚类分离测度)
1.这篇论文要解决什么问题?要验证一个什么科学假设?
问题是确定数据中聚类的适当数量,解决这种问题的两种方法都取决于确定指数中相对较大的变化,而不是指数的最小化或最大化,因此,一般来说,需要人为解释和主观分析什么是参数中的“较大变化”。
两种方法:一种常用的技术依赖于针对多个簇绘制优化参数,并选择参数值发生较大变化的簇数作为最佳值。
第二种方法是分层的等级技术,通常寻求组间融合的较大变化。
2.这篇论文有哪些相关研究,这些研究是怎么分类的?有哪些研究员值得关注?
3、论文中提到的解决方案是什么,关键点在哪儿?提出了一种度量,它表示假设具有数据密度的聚类的相似性,该数据密度是距离聚类的向量特征的递减函数。该度量可用于推断数据分区的适当性,因此可用于比较数据的各种划分的相对适当性。该措施既不依赖于分析的聚类数,也不依赖于数据分区的方法,并且可以用于指导聚类搜索算法。提出了一个新的聚类参数,该参数的最小化似乎表明数据集的自然分区。

这个定义中,aki是向量ai的第k个分量,而ai是第i个聚类的质心。简单来说,质心是一个聚类中所有数据点的平均值向量。
举个例子来说明:假设我们有一个二维数据集,包含以下数据点:
(1, 2), (3, 4), (5, 6), (7, 8), (9, 10)
现在我们将这些数据点分为两个聚类,第一个聚类包含前三个数据点,第二个聚类包含后两个数据点。
对于第一个聚类的质心,我们计算每个维度的平均值,即(1+3+5)/3 = 3和(2+4+6)/3 = 4。所以第一个聚类的质心是(3, 4)。
对于第二个聚类的质心,我们计算每个维度的平均值,即(7+9)/2 = 8和(8+10)/2 = 9。所以第二个聚类的质心是(8, 9)。
在这个例子中,aki表示第i个聚类的质心向量ai的第k个分量。

R的意义在于,它是每个聚类与其最相似聚类的相似性度量的系统范围平均值。因此,聚类的“最佳”选择将是使这种平均相似性最小化的聚类。
当p = 2时,Mij是质心之间的欧几里得距离。如果q = 1,则Si成为聚类i中的向量到聚类i的质心的平均欧几里得距离。如果q = 2,则Si是聚类中的样本到相应聚类中心的距离的标准偏差。如果p = q = 2,则Rij是为聚类i和j计算的经典Fisher相似性度量的倒数。
4、论文中的实验是如何设计的?各个实验分别得到了什么结论?
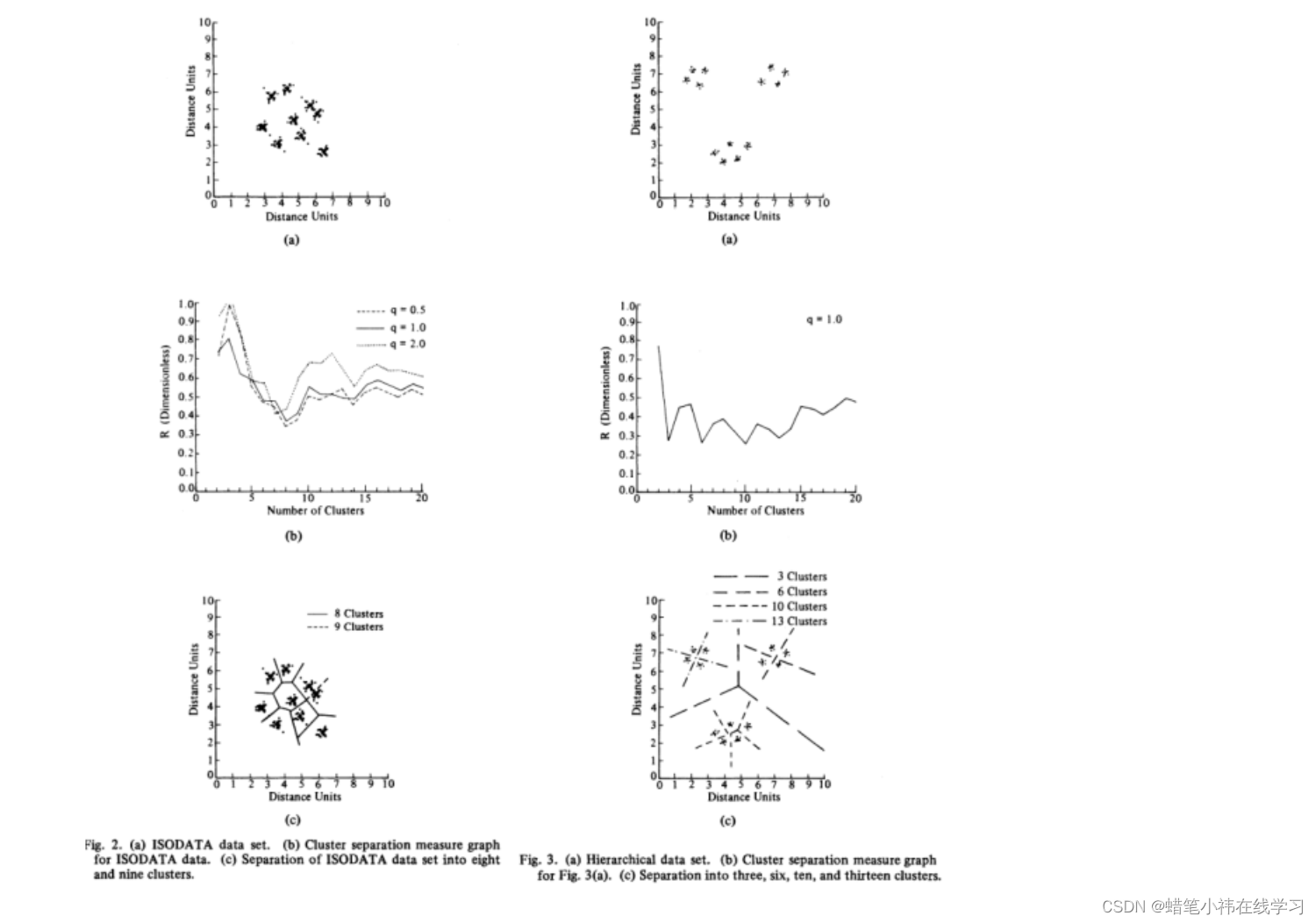
图2(a)示出了改编自Ball和Hall的集群系统测试集的225个点的数据集。图2(b)的相关曲线图示出了对于q = 0.5、1.0、2.0和p = 2.0的最小20个K值的k的性能。如图2(b)所示,当K = 8时,R最小,当K = 9时,R值大约大10%。
图3(a)和3(b)显示了130个点的数据集及其相关的R图。对应于R的四个局部最小值的分区在图3(c)中指示。在K = 3、6、10和13处,R的局部最小值近似相等,这是由于13个小簇中的每一个的密度大致相等,而它们在大簇中的间隔近似相等。聚类分离度量表明相邻的小聚类与大聚类具有大致相同的相似性。

图4中110个数据点和相关的k图显示在图4(a)和图4(B),其中三个组分区被选择为最佳,由虚线指示。随后对分配给第三组的那些点进行分析。图4(c)中示出了相关的R曲线图,而图4(a)中的细虚线示出了指示为最佳的分离。值得注意的是,图4(c)中的最小R高于图4(b)中的最小R。如果不是这种情况,图4(a)中的聚类3将在全局数据集的最佳划分中被细分。
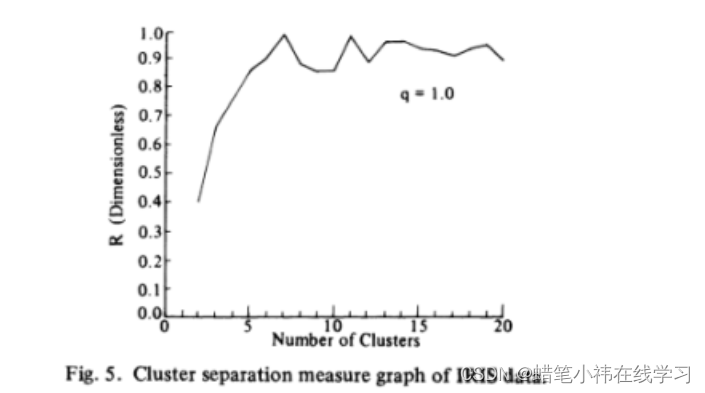
图5中R是针对Fisher在一系列统计检验中使用的四维鸢尾数据计算的。四个测量的每一个50名成员的三个品种的花鸢尾Setosa,鸢尾Versicolor,和鸢尾Virginica。已知Iris Setosa可线性分离,其他两个鸢尾Virginica和鸢尾Versicolor有相当大的重叠。如图5所示,选择K = 2作为数据的最佳划分,而在K = 9和K = 17处发现R的局部最小值。
5、这篇论文到底有什么贡献?(三句话内说明)新在什么地方?
聚类分析通常是数据分析的第一步,要求用户向分析系统提供参数值,例如最小可接受的聚类距离或最小可接受的标准偏差, “所有聚类算法的一个共同缺点是它们的性能高度依赖于用户设置的各种参数。事实上,“适当”的设置通常只能通过试验和错误的方法来确定。如果将其纳入聚类搜索算法中,这里提出的度量基本上克服了这一困难,因为它只需要用户指定p和q指数,这相当于只需要用户指定要使用的距离和分散度量。