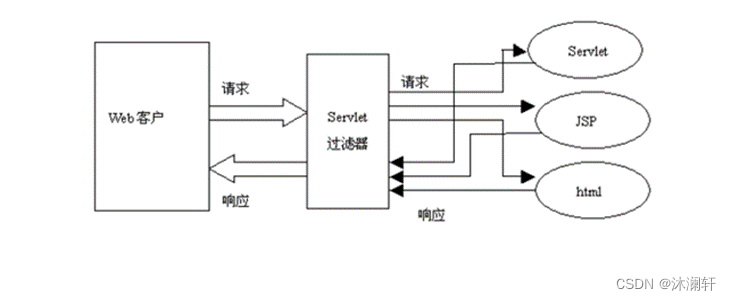
上一篇中讨论了一般性的原则,这里我们具体讨论通过时间反向传播(backpropagation through time,BPTT)的细节。我们将展示目标函数对于所有模型参数的梯度计算方法。
出于简单的目的,我们以一个没有偏置参数的循环神经网络,其在隐藏层中的激活函数使用恒等函数()。
对于时间步,单个样本的输入及其标签分别为
和
。计算隐状态
和输出
的公式为
其中,权重参数为,
和
。
目标函数为:
。
通常,训练这个模型需要对这些参数分别进行梯度计算:、
和
。
其中:
从中可以看到,这个简单的线性例子已经展现出长序列模型的一些关键问题:
它陷入到了的潜在的非常大的指数幂。在这个指数幂中,小于1的特征值将会消失(出现梯度消失),大于1的特征值将会发散(出现梯度爆炸)。