【零基础入门】凸优化1：怎么培养研究能力，从模型+优化开始！

凸优化1

优化问题的形式
优化问题类别1：凸函数和非凸函数
优化问题类别2：带条件和无条件
优化问题类别3：离散和连续
优化问题类别4：平滑和非平滑
如何判断一个目标函数是凸函数，还是非凸函数？
怎么设计模型为凸函数？
怎么求解非凸函数？
怎么对非凸函数松弛，变成凸函数？

基本上，机器学习就是模型 + 优化。

重要性亦如，程序 = 数据结构 + 算法，缺一不可。

如果你只学模型，你就缺了一条腿，走的不稳不快，没核心竞争力。

学了凸优化，看论文就会很轻松，就能理解数学公式在做什么，就喜欢看数学公式了。

就和别的数学不一样，你学了在应用里基本用不到，但你会凸优化，你可以根据任务改更好的损失函数、在原有模型上创新。

应用优化、科研论文必备。

优化问题的形式

任何一个优化问题都可以写成：

$Minimizef_{0}(x) \\f_{i}<=0, \\g_{j}(x)=0.$

$Minimize f_0(x)$ : 这是凸优化问题的目标，表示我们的目的是找到一个变量x的值，使得函数 $f_0(x)$ 的值尽可能小。
$f_i(x) <= 0$ : 这些是所谓的不等式约束。 $f_i(x)$ 表示不同的函数，每个函数都有一个对应的不等式。i的范围是从1到某个整数，它表示有多少个这样的约束。这些约束限制了解决方案的可行性，即我们不能随便选择任何值来最小化 $f_0(x)$ ；解决方案必须使所有的 $f_i(x)$ 都小于或等于0。
$g_j(x) = 0$ : 是等式约束，用 $g_j(x)$ 表示。j的范围同样表示有多少个这样的约束。等式约束必须被严格遵守，意味着解决方案必须使所有的 $g_j(x)$ 恰好等于0。

将这些信息放在一起，我们可以这样理解这个公式：我们的目标是找到一组变量x的值，这组值不仅要使目标函数 $f_0(x)$ 的值最小化，而且还要满足所有的不等式约束 $f_i(x) <= 0$ 和所有的等式约束 $g_j(x) = 0$ 。

这就像是你在玩一场游戏，目标是得分最低（最小化f_0(x)），同时你必须遵守游戏的规则（满足不等式和等式约束）。

优化问题类别1：凸函数和非凸函数

想象山的形状，就像一个凸形的曲线。

如果你在凸形的曲线里面放一个小球，无论小球在哪个位置，它最终都会滚到最低点。

在数学中，这个凸形的曲线就可以用凸函数来描述。

凸函数的优化问题非常重要，因为它们通常有唯一的最低点（全局最小值），就像碗底一样。

所以，当你的目标是最小化一个凸函数时，你可以使用任意的算法（比如梯度下降法）来寻找这个全局最小值，而不用担心找到一个“伪”最小值（局部最小值）。

但如果是非凸函数，会有很多局部最小值，要选择合适的算法，但也不容易找到全局最小值。

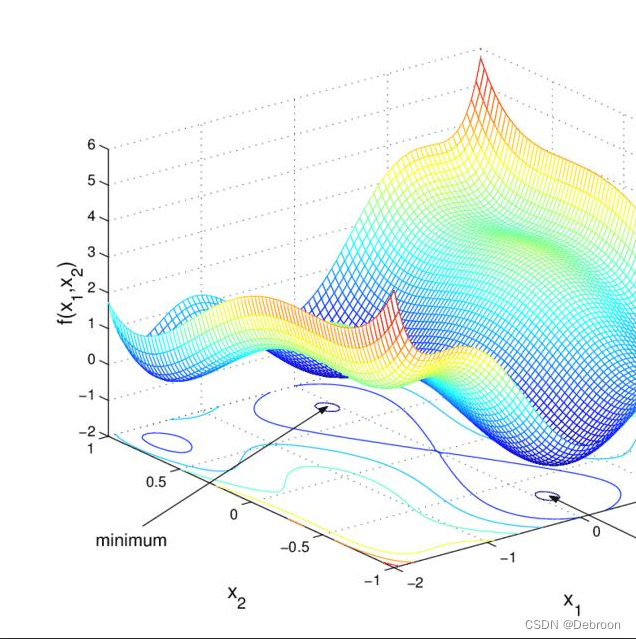
在处理非凸函数优化时，可以采取以下几种策略：

局部搜索方法：这类方法从某个初始点出发，通过迭代的方式尝试找到局部最优解。例如梯度下降、牛顿法等。它们通常会收敛到最近的局部最小值，但不保证找到全局最小值。
全局优化算法：这些算法旨在搜索整个函数空间以找到全局最小值。例如模拟退火、遗传算法、粒子群优化等。这些方法可能会消耗更多的计算资源，但更有可能接近或找到全局最优解。
启发式方法：这类方法包括对问题的特殊理解和创造性的算法设计，如分枝定界、割平面方法等。它们通常利用问题的特定结构来缩小搜索范围并找到更好的解。
凸松弛：当面对一个难以直接解决的非凸问题时，可以尝试将其松弛为一个凸问题，例如通过引入额外的变量或者放松一些约束条件。这样虽然可能无法得到原问题的精确解，但可以获得一个近似解，有时这个近似解足够接近真实的全局最优解。
集成方法：将上述方法组合使用，例如先用全局优化算法找到一个不错的起点，然后再使用局部搜索方法进行精细调整。

优化问题类别2：带条件和无条件

这种类别的优化问题就像是你在玩一个游戏，但是有一些规则限制你的动作。

在数学中，这些规则被称为约束条件。

这些约束可以是等式（比如，你需要在一个特定的预算内花费），也可以是不等式（比如，你不能超过一定的重量或体积）。

当你的目标是找到某个函数的最大值或最小值，但同时要满足一些额外的条件时，你就面临着一个带条件的优化问题。

这种问题需要特别的技巧来解决，因为你不能只关注函数值的优化，还要确保所有的约束都得到满足。

线性规划和非线性规划就是处理这类问题的常用方法。

优化问题类别3：离散和连续

这个类别的区分是根据优化问题的变量是离散的还是连续的。

离散就像计数一样，你可以数1、2、3，但不能数1.5、2.5等。

而连续则像用尺子量长度一样，可以量到任何小数点后的值。

离散优化问题通常涉及整数、图或网络等，在这类问题中，变量只能取有限的、分开的值。

举个例子，旅行商问题就是一个经典的离散优化问题，你需要找到一条路径，经过一系列城市一次且仅一次，并最终回到起点，同时路径长度最短。

连续优化问题中，变量可以在某个区间内任意取值。

比如，在设计一座桥时，你可能会调整桥的长度、宽度和曲率，这些都是连续的变量，你需要找到最佳的组合，以确保桥既安全又经济。

优化问题类别4：平滑和非平滑

平滑优化问题是指目标函数具有良好的数学性质，特别是它们在定义域内是连续可导的，这意味着它们有着连续的梯度（或者说斜率）。

你画这样一个函数的图像，你会得到一个光滑的曲线或曲面，没有任何尖锐的拐点或者断点。

这种光滑性让函数容易使用基于梯度的方法来优化，因为你可以通过计算梯度（梯度下降法或牛顿法等）来找到函数值上升或下降最快的方向。

常见的平滑函数包括多项式函数、指数函数和对数函数。

非平滑优化问题中的目标函数可能不是处处连续可导的，这意味着函数的图像可能有尖角、棱角或者不连续的跳跃。

你画这样一个函数的图像，你的笔在某些点上可能需要“跳过”一个间断，或者在转角处突然改变方向。

非平滑优化问题通常更难处理，因为没有连续的梯度信息可以指导优化过程，因此可能需要使用更复杂的算法，如次梯度方法、近似梯度方法或者基于非梯度的优化策略或启发式算法来求解。

常见的例子包括绝对值函数、最大值/最小值函数（如ReLU激活函数）。

最简单的情况是：无条件、凸函数、连续、平滑，这种情况特别好算的。

像其他复杂的情况，那需要学习各个优化算法了。

如何判断一个目标函数是凸函数，还是非凸函数？

判断一个函数是凸函数还是非凸函数可以采用以下两种方法：

通过二阶导数
利用凸性定义

方法一：通过二阶导数判断

对于一元函数，可以通过判断其二阶导数的符号来判断函数的凸性：

如果函数的二阶导数在定义域内始终大于等于零（即非负），则该函数是凸函数。
如果函数的二阶导数在定义域内始终小于等于零（即非正），则该函数是凹函数。

对于多元函数，可以通过计算其海森矩阵（Hessian Matrix）来判断函数的凸性：

如果海森矩阵在定义域内始终半正定（即所有特征值非负），则该函数是凸函数。
如果海森矩阵在定义域内始终半负定（即所有特征值非正），则该函数是凹函数。

方法二：利用凸性定义

函数的凸性定义如下：

对于一元函数，如果对于任意的 x1、x2 ∈ 定义域内，以及任意的 t ∈ [0, 1]，都有 $f (t x 1 + (1 - t) x 2) \leq t f (x 1) + (1 - t) f (x 2)$ ，则该函数是凸函数。
对于多元函数，如果对于任意的 x1、x2 ∈ 定义域内，以及任意的 t ∈ [0, 1]，都有 $f (t x 1 + (1 - t) x 2) \leq t f (x 1) + (1 - t) f (x 2)$ ，则该函数是凸函数。