逻辑回归(LR,Logistic Regression)算法
当线性回归的预测结果,由于受到个别极端数值的影响而不准的时候, 可以用逻辑回归来解决.
逻辑回归模型的输出只能在 0 到 1 之间,也就是表达一个事件会发生的概率,所以被广泛地应用在分类问题上。
平滑函数
平滑函数: 把线性回归预测到的具体的值,通过一个函数转化成为 0~1 的一个概率值.
常见的平滑函数:
- 高斯函数(Gaussian Function)
- sigmoid 函数
- tanh 函数
- B样条函数(B-Spline Function)
- Loess 平滑函数
- 移动平均(Moving Average)
点击查看平滑函数详情: https://blog.csdn.net/galoiszhou/article/details/135133991
损失函数
逻辑回归的损失函数通常是对数损失函数(Logarithmic Loss),也称为对数似然损失(Log-Likelihood Loss)或交叉熵损失(Cross-Entropy Loss)。
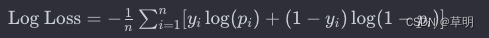
n是样本数量。yi是样本 i 的实际标签(1 表示正例,0 表示负例)。pi是模型对样本 i 预测为正例的概率。
对数损失函数的目标是最小化模型对于正例和负例的预测概率与实际标签之间的差异。当模型的预测概率与实际标签一致时,对数损失趋近于0。随着预测概率与实际标签的差异增大,对数损失逐渐增大。
逻辑回归算法的优点:
- 继承了线性回归算法的全部优点
- 运算效率高
- 可解释性强
- 减少了极端值对于整体分布的影响, 让整体的分布更加集中
逻辑回归算法的缺点:
- 如果事物不是简单的线性分布, 则结果也不会很理想
逻辑回归算法的适用场景:
- 二分类问题
- 逻辑回归最适用于解决二分类问题,其中目标是将实例划分为两个类别,如正例和负例。
- 线性可分数据
- 当数据在特征空间中呈现线性可分布时,逻辑回归通常表现较好。这意味着可以通过一条直线将两个类别分开。
- 高维数据
- 逻辑回归在高维数据集上的表现通常较好,尤其是当特征的数量相对较大时。
- 概率建模
- 当任务需要建模概率时,例如对某个事件发生的概率进行预测,逻辑回归是一个自然的选择。
- 特征之间相对独立
- 逻辑回归假设特征之间相对独立,因此在特征之间存在共线性的情况下,可能需要额外的处理或者考虑其他算法。
- 噪声较小
- 逻辑回归对噪声相对不敏感,因此在数据相对干净的情况下,表现较好。
- 大规模数据集
- 逻辑回归的计算开销相对较小,适用于大规模数据集。
- 可解释性需求
- 逻辑回归提供了直观的可解释性,可以理解各个特征对预测的影响程度,因此在可解释性要求较高的场景中很有用。
- 快速原型开发
- 由于逻辑回归的简单性和高效性,它是快速原型开发的好选择,特别是当问题的复杂性不要求使用更复杂的模型时。
逻辑回归算法的案例:
- 垃圾邮件过滤
- 逻辑回归常用于垃圾邮件过滤,通过分析邮件内容和发送者的特征,预测邮件是否是垃圾邮件。
- 疾病预测
- 在医学领域,逻辑回归可用于预测患者是否患有某种疾病,基于患者的医疗历史、生活习惯等特征。
- 信用评分
- 逻辑回归在信用评分模型中得到广泛应用,用于预测借款人是否会违约,从而帮助银行和金融机构评估风险。
- 广告点击率预测
- 在在线广告领域,逻辑回归可用于预测用户是否会点击某个广告,以优化广告投放策略。
- 客户流失预测
- 逻辑回归可以用于预测客户是否有流失的风险,帮助企业采取措施留住客户。
- 人才招聘
- 在招聘领域,逻辑回归可用于预测求职者是否适合特定的职位,以辅助招聘决策。
- 社交网络分析
- 逻辑回归可以用于社交网络中的分析,例如预测用户是否会在社交平台上分享某种类型的内容。
- 电商推荐系统
- 在电商领域,逻辑回归可用于个性化推荐系统,预测用户是否对某个产品感兴趣。
- 网络安全
- 逻辑回归可以用于网络安全中的异常检测,例如预测网络中是否存在异常登录行为。
- 学生成功预测
- 在教育领域,逻辑回归可用于预测学生是否能够成功完成某门课程,帮助学校提供个性化的教育支持。