B. Phoenix and Beauty
这道题目学到的东西:
- 从给出的数据范围观察,得到一些有用信息(峰哥教的)
- 考虑无解的情况‘
其实这题考虑怎么操作是比较难的,如果能想出来满足条件的结果就比较好了(我在说什么我自己也不知道,算了直接看下面的图吧)
假设
k
=
3
k=3
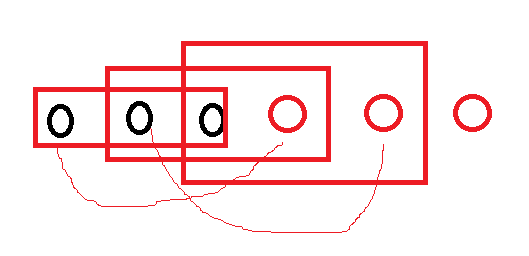
k=3,下面是我们得到的结果数列,任意连续k个都相等,那么我们每次让这个框移动一次新进来的数和出去的数应该是一样的,然后一直这样移动,可以发现,当移动三次,前三个数中的每个数和后面三个数对应位置相同,出现了循环,循环节是3,至此就发现了这道题目最重要的性质。
我们考虑什么情况无解,当出现的不同的数大于k的话就没办法构造出以k为循环节的答案,这种情况是无解的。
下面考虑如何构造,观察
n
∗
k
<
m
n*k<m
n∗k<m所以我们将长度为k的数组复制n次即可,如果不同的数不足k个我们任意加进去没出现过的且小于n的数补满k即可
#include <bits/stdc++.h>
#define rep(i,a,b) for(register int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(register int i = (a); i >= (b); --i)
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define db double
#define endl '\n'
#define debug(a) cout<<#a<<"="<<a<<endl;
#define IOS ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define INF 0x3f3f3f3f
using namespace std;
const int N = 1e4+10;
int t;
int a[110], b[N];
void solve()
{
set<int>s;
int n,k; cin >> n >> k;
rep(i,1,n) cin >> a[i], s.insert(a[i]);
if(s.size()>k)
{
cout << "-1" << endl;
return;
}
int j=1;
while(s.size()<k)
{
while(j<=n&&s.count(j)==1) j++;
s.insert(j);
}
cout << n*k << endl;
rep(i,1,n) for(auto x:s) cout << x << ' ';
cout << endl;
}
int main()
{
IOS
// freopen("1.in", "r", stdin);
cin >> t;
while(t --)
solve();
return 0;
}