给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

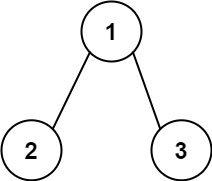
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

递归

可以使用深度优先遍历的方式来遍历二叉树

确定递归函数的参数和返回类型

参数：需要二叉树的根节点，还需要一个计数器，这个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。

• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。

• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。

而本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回，那么返回类型是什么呢？

遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用bool类型表示。

所以代码如下：

boolean traversal(TreeNode cur,int targetSum)

确定终止条件

不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。

如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。

如果遍历到了叶子节点，count不为0，就是没找到。

递归终止条件代码如下：

if(cur.left==null && cur.right==null && targetSum==0) return true;
if(cur.left==null && cur.right==null) return false;

确定单层递归的逻辑

因为终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。

递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

代码如下：

if(cur.left!=null) { // 左 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    targetSum-=cur.left.val;
    if(traversal(cur.left,targetSum)) return true; // 注意这里有回溯的逻辑
}
if(cur.right!=null){ // 右 （空节点不遍历）
    // 遇到叶子节点返回true，则直接返回true
    targetSum-=cur.right.val;
    if(traversal(cur.right,targetSum)) return true; // 注意这里有回溯的逻辑
}
return false;

以上代码中是包含着回溯的，没有回溯，如何后撤重新找另一条路径呢。

回溯隐藏在targetSum这里， 因为把targetSum-=cur.right.val; 直接作为参数传进去，函数结束，targetSum的数值没有改变。

为了把回溯的过程体现出来，可以改为如下代码：

if(cur.left!=null){
    targetSum-=cur.left.val;
    if(traversal(cur.left,targetSum)) return true;
    targetSum+=cur.left.val;
}
if(cur.right!=null){
    targetSum-=cur.right.val;
    if(traversal(cur.right,targetSum)) return true;
    targetSum+=cur.right.val;
}
return false;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null) return false;
        return traversal(root,targetSum-root.val);
    }
    boolean traversal(TreeNode cur,int targetSum){
        if(cur.left==null && cur.right==null && targetSum==0) return true;
        if(cur.left==null && cur.right==null) return false;
        if(cur.left!=null){
            targetSum-=cur.left.val;
            if(traversal(cur.left,targetSum)) return true;
            targetSum+=cur.left.val;
        }
        if(cur.right!=null){
            targetSum-=cur.right.val;
            if(traversal(cur.right,targetSum)) return true;
            targetSum+=cur.right.val;
        }
        return false;
    }
}

迭代

如果使用栈模拟递归的话，那么如果做回溯呢？

此时栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。

class solution {
    public boolean haspathsum(treenode root, int targetsum) {
        if(root == null) return false;
        stack<treenode> stack1 = new stack<>();
        stack<integer> stack2 = new stack<>();
        stack1.push(root);
        stack2.push(root.val);
        while(!stack1.isempty()) {
            int size = stack1.size();
​
            for(int i = 0; i < size; i++) {
                treenode node = stack1.pop();
                int sum = stack2.pop();
​
                // 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
                if(node.left == null && node.right == null && sum == targetsum) {
                    return true;
                }
                // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if(node.right != null){
                    stack1.push(node.right);
                    stack2.push(sum + node.right.val);
                }
                // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if(node.left != null) {
                    stack1.push(node.left);
                    stack2.push(sum + node.left.val);
                }
            }
        }
        return false;
    }
}